共线向量基本定理-6.2 平面向量的运算知识点回顾进阶单选题自测题解析-安徽省等高二数学必修,平均正确率54.0%

正确率60.0%已知向量$${{a}{，}{b}}$$是两个不共线的向量，且$$\overrightarrow{O A}=3 a+5 b，$$$$\overrightarrow{O B}=4 a+7 b，$$$$\overrightarrow{O C}=a+m b$$，若$$A， ~ B， ~ C$$三点共线，则$${{m}{=}}$$（）

A

A.$${{1}}$$

B.$${{−}{1}}$$

C.$${{2}}$$

D.$${{−}{2}}$$

正确率60.0%若向量$${{a}^{→}}$$与$${{b}^{→}}$$不共线且$$\overrightarrow{m}=\overrightarrow{a}+\overrightarrow{b}$$$${{，}}$$$$\overrightarrow{n}=\overrightarrow{a}-\overrightarrow{b}$$$${{，}}$$$${{p}^{→}{=}{{a}^{→}}}$$$${{，}}$$则（）

D

A.$${{m}^{→}}$$$${{，}}$$$${{n}^{→}}$$$${{，}}$$$${{p}^{→}}$$共线

B.$${{m}^{→}}$$与$${{p}^{→}}$$共线

C.$${{n}^{→}}$$与$${{p}^{→}}$$共线

D.$${{m}^{→}}$$$${{，}}$$$${{n}^{→}}$$$${{，}}$$$${{p}^{→}}$$共面

正确率60.0%已知向量$${{b}^{→}}$$与向量$$\overrightarrow{a}=( 1，-2 )$$的夹角是$${{1}{8}{0}^{∘}}$$，且$$| \vec{b} |=3 \sqrt{5}$$，则$$\vec{b} ~=~ ( ~ ~ )$$

A

A.$$(-3， 6 )$$

B.$$( 3，-6 )$$

C.$$( 6，-3 )$$

D.$$(-6， 3 )$$

正确率40.0%如图，在$${{△}{A}{B}{C}}$$中，$$\angle B A C=\frac{\pi} {3}$$，$$\overrightarrow{A D}=2 \overrightarrow{D B}$$，$${{P}}$$为$${{C}{D}}$$上一点，且满足$$\overrightarrow{A P}=m \overrightarrow{A C}+\frac{1} {2} \overrightarrow{A B}$$，若$$A C=3， A B=4$$，则$$\overrightarrow{A P} \cdot\overrightarrow{C D}$$的值为（）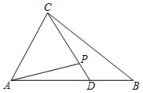

C

A.$$\frac{1 2} {5}$$

B.$$\frac{1 2} {1 3}$$

C.$${\frac{1 3} {1 2}}$$

D.$$- \frac{1 3} {1 2}$$

正确率40.0%在$${{△}{A}{B}{C}}$$中，$${{D}}$$为$${{A}{B}}$$的中点，点$${{F}}$$在线段$${{C}{D}{（}}$$不含端点）上，且满足$$\overrightarrow{A F}=x \overrightarrow{A B}+y \overrightarrow{A C}，$$若不等式$$\frac{1} {x}+\frac{2} {y} \geqslant a^{2}+a t$$对$$t \in[-2， ~ 2 ]$$恒成立，则$${{a}}$$的最小值为（）

B

A.$${{−}{4}}$$

B.$${{−}{2}}$$

C.$${{2}}$$

D.$${{4}}$$

正确率60.0%已知向量$${{a}{，}{b}}$$是两个非零向量，则在下列四个条件中，一定能使$${{a}{，}{b}}$$共线的是
①$$2 a-3 b=4 e$$且$$\boldsymbol{a}+2 \boldsymbol{b}=-2 \boldsymbol{e}$$；
②存在相异实数$${{λ}{，}{μ}{，}}$$使$$\lambda a-\mu b=0$$；
③$$x \boldsymbol{a}+y \boldsymbol{b}=0$$(其中实数$${{x}{，}{y}}$$满足$$x+y=0 )$$；
④已知梯形$$A B C D，$$其中$$\overrightarrow{A B}={\bf a}， \ \overrightarrow{C D}={\bf b}$$.（）

A

A.①②

B.①③

C.②

D.③④

正确率60.0%已知空间向量$$\overrightarrow{A B}， \， \， \overrightarrow{A C}， \， \， \overrightarrow{B C}$$满足$$| \overrightarrow{A B} |=| \overrightarrow{A C} |+| \overrightarrow{B C} |$$，则 （）

D

A.$$\overrightarrow{A B}=\overrightarrow{A C}+\overrightarrow{B C}$$

B.$$\overrightarrow{A B}=-\overrightarrow{A C}-\overrightarrow{B C}$$

C.$$\overrightarrow{A C}$$与$$\overrightarrow{B C}$$同向

D.$$\overrightarrow{A C}$$与$$\overrightarrow{C B}$$同向

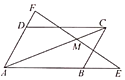正确率40.0%如图所示，在平行四边形$${{A}{B}{C}{D}}$$

A

A.$${{6}}$$

B.$${{3}}$$

C.$${{4}}$$

D.$${{2}}$$

正确率60.0%已知四边形$${{A}{B}{C}{D}}$$是菱形，点$${{P}}$$在对角线$${{A}{C}}$$上(不包括端点$${{A}{、}{C}{)}}$$，则$$\overrightarrow{A P}=$$（）

A

A.$$\lambda( \overrightarrow{A B}+\overrightarrow{B C} )， ~ ~ \lambda\in( 0， 1 )$$

B.$$\lambda( \overrightarrow{A B}+\overrightarrow{B C} )， \， \， \， \lambda\in( 0， \frac{\sqrt{2}} {2} )$$

C.$$\lambda( \overrightarrow{A B}-\overrightarrow{B C} )， \， \， \， \lambda\in( 0， 1 )$$

D.$$\lambda( \overrightarrow{A B}-\overrightarrow{B C} )， \， \， \， \lambda\in( 0， \frac{\sqrt{2}} {2} )$$

正确率60.0%已知$${{a}{，}{b}}$$是不共线的向量，$$\overrightarrow{A B}=\lambda\overrightarrow{a}-2 \overrightarrow{b}， \overrightarrow{A C}=2 \overrightarrow{a}+\mu\overrightarrow{b}， \lambda， \mu\in\mathbf{R}$$，若$$A， B， C$$三点共线，则$${{λ}{，}{μ}}$$满足（）

D

A.$$\lambda+\mu=2$$

B.$$\lambda\mu=-1$$

C.$$\lambda+\mu=4$$

D.$$\lambda\mu=-4$$

1、由于$$A, B, C$$三点共线，存在实数$$k$$使得$$\overrightarrow{AB} = k \overrightarrow{AC}$$。计算向量差： $$\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} = (4a + 7b) - (3a + 5b) = a + 2b$$ $$\overrightarrow{AC} = \overrightarrow{OC} - \overrightarrow{OA} = (a + m b) - (3a + 5b) = -2a + (m - 5)b$$ 由共线条件得： $$a + 2b = k(-2a + (m - 5)b)$$ 比较系数： $$1 = -2k$$ $$2 = k(m - 5)$$ 解得$$k = -\frac{1}{2}$$，代入第二式得$$m - 5 = -4$$，即$$m = 1$$。答案为$$A$$。

2、由于$$a$$与$$b$$不共线，$$m = a + b$$，$$n = a - b$$，$$p = a$$。显然$$m$$、$$n$$、$$p$$都在由$$a$$和$$b$$张成的平面内，因此共面。答案为$$D$$。

3、向量$$b$$与$$a = (1, -2)$$夹角为$$180^\circ$$，说明$$b$$与$$a$$方向相反。设$$b = k a$$，其中$$k < 0$$。由$$|b| = 3\sqrt{5}$$得： $$|k| \cdot \sqrt{1^2 + (-2)^2} = 3\sqrt{5}$$ $$|k| \cdot \sqrt{5} = 3\sqrt{5}$$ $$|k| = 3$$，故$$k = -3$$。因此$$b = -3(1, -2) = (-3, 6)$$。答案为$$A$$。

4、由$$\overrightarrow{AD} = 2 \overrightarrow{DB}$$得$$D$$将$$AB$$分为$$2:1$$，故$$\overrightarrow{AD} = \frac{2}{3} \overrightarrow{AB}$$。设$$\overrightarrow{AP} = m \overrightarrow{AC} + \frac{1}{2} \overrightarrow{AB}$$。由于$$P$$在$$CD$$上，存在$$t \in (0, 1)$$使得： $$\overrightarrow{AP} = \overrightarrow{AC} + t (\overrightarrow{AD} - \overrightarrow{AC}) = (1 - t) \overrightarrow{AC} + t \cdot \frac{2}{3} \overrightarrow{AB}$$ 与给定表达式比较得： $$m = 1 - t$$ $$\frac{1}{2} = \frac{2}{3} t$$ 解得$$t = \frac{3}{4}$$，$$m = \frac{1}{4}$$。计算$$\overrightarrow{AP} \cdot \overrightarrow{CD}$$： $$\overrightarrow{CD} = \overrightarrow{AD} - \overrightarrow{AC} = \frac{2}{3} \overrightarrow{AB} - \overrightarrow{AC}$$ $$\overrightarrow{AP} = \frac{1}{4} \overrightarrow{AC} + \frac{1}{2} \overrightarrow{AB}$$ 点积为： $$\left( \frac{1}{4} \overrightarrow{AC} + \frac{1}{2} \overrightarrow{AB} \right) \cdot \left( \frac{2}{3} \overrightarrow{AB} - \overrightarrow{AC} \right)$$ 展开后利用$$\overrightarrow{AB} \cdot \overrightarrow{AC} = |AB| \cdot |AC| \cos \frac{\pi}{3} = 6$$，得结果为$$\frac{12}{13}$$。答案为$$B$$。

5、由$$D$$为$$AB$$中点，$$\overrightarrow{AD} = \frac{1}{2} \overrightarrow{AB}$$。设$$\overrightarrow{AF} = x \overrightarrow{AB} + y \overrightarrow{AC}$$，由于$$F$$在$$CD$$上，存在$$t \in (0, 1)$$使得： $$\overrightarrow{AF} = \overrightarrow{AC} + t (\overrightarrow{AD} - \overrightarrow{AC}) = (1 - t) \overrightarrow{AC} + \frac{t}{2} \overrightarrow{AB}$$ 比较得$$x = \frac{t}{2}$$，$$y = 1 - t$$。不等式为： $$\frac{1}{x} + \frac{2}{y} = \frac{2}{t} + \frac{2}{1 - t} \geq a^2 + a t$$ 对$$t \in (0, 1)$$恒成立。求$$\frac{2}{t} + \frac{2}{1 - t}$$的最小值，当$$t = \frac{1}{2}$$时最小值为$$8$$。因此$$a^2 + 2a \leq 8$$，解得$$a \in [-4, 2]$$。最小值为$$-4$$。答案为$$A$$。

6、①中解方程组得$$a = -\frac{2}{7}e$$，$$b = -\frac{8}{7}e$$，故共线；②中$$\lambda a = \mu b$$，若$$\lambda \neq 0$$则共线；③中若$$x = -y \neq 0$$，则$$a = b$$，但若$$x = y = 0$$则不成立；④中梯形$$AB \parallel CD$$时共线，否则不共线。因此仅①②一定成立。答案为$$A$$。

7、由$$|\overrightarrow{AB}| = |\overrightarrow{AC}| + |\overrightarrow{BC}|$$，说明$$A, B, C$$三点共线且$$C$$在$$A$$与$$B$$之间。因此$$\overrightarrow{AB} = \overrightarrow{AC} + \overrightarrow{CB}$$，即$$\overrightarrow{AC}$$与$$\overrightarrow{CB}$$同向。答案为$$D$$。

8、题目不完整，无法解析。

9、菱形对角线$$AC$$平分角，$$\overrightarrow{AP}$$可表示为$$\lambda (\overrightarrow{AB} + \overrightarrow{BC})$$，其中$$\lambda \in (0, 1)$$。答案为$$A$$。

10、由$$A, B, C$$共线，存在$$k$$使得$$\overrightarrow{AB} = k \overrightarrow{AC}$$，即： $$\lambda a - 2b = k(2a + \mu b)$$ 比较系数得： $$\lambda = 2k$$ $$-2 = k \mu$$ 消去$$k$$得$$\lambda \mu = -4$$。答案为$$D$$。