正确率60.0%在$${{△}{A}{B}{C}}$$中,$$\overrightarrow{A E}=\frac{3} {1 0} \cdot( \overrightarrow{A B}+\overrightarrow{A C} )$$,$${{D}}$$为$${{B}{C}}$$边的中点,则()
C
A.$$3 \overrightarrow{A E}=7 \overrightarrow{E D}$$
B.$$7 \overrightarrow{A E}=3 \overrightarrow{E D}$$
C.$$2 \overrightarrow{A E}=3 \overrightarrow{E D}$$
D.$$3 \overrightarrow{A E}=2 \overrightarrow{E D}$$
2、['向量加法的定义及运算法则', '向量减法的定义及运算法则']正确率60.0%若$${{A}{B}{C}{D}}$$是正方形,$${{E}}$$是$${{C}{D}}$$的中点,且$$\overrightarrow{A B}=\overrightarrow{a}, \, \, \overrightarrow{A D}=\overrightarrow{b},$$则$$\overrightarrow{B E}=( \eta)$$
B
A.$$\vec{b}+\frac{1} {2} \vec{a}$$
B.$$\vec{b}-\frac{1} {2} \vec{a}$$
C.$$\overrightarrow{a}+\frac{1} {2} \overrightarrow{b}$$
D.$$\overrightarrow{a}-\frac{1} {2} \overrightarrow{b}$$
3、['向量加法的定义及运算法则', '向量数乘的定义与运算律']正确率40.0%在$${{△}{A}{B}{C}}$$中,$${{D}}$$在三角形所在平面内一点,且$$\overrightarrow{A D}=\frac{1} {3} \overrightarrow{A B}+\frac{1} {2} \overrightarrow{A C},$$则$${\frac{S_{\triangle A B D}} {S_{\triangle A B C}}}={(}$$)
B
A.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
B.$$\frac{1} {2}$$
C.$$\frac{1} {3}$$
D.$$\frac{1} {6}$$
4、['向量加法的定义及运算法则', '数量积的性质', '数量积的运算律', '向量的数量积的定义']正确率60.0%在$${{△}{A}{B}{C}}$$中,$$| B C |=4, \quad( \overrightarrow{A B}+\overrightarrow{A C} ) \cdot\overrightarrow{B C}=0$$,则$$\overrightarrow{B A} \cdot\overrightarrow{B C}=\emptyset$$)
D
A.$${{4}}$$
B.$${{−}{4}}$$
C.$${{−}{8}}$$
D.$${{8}}$$
5、['向量加法的定义及运算法则', '平面向量基本定理']正确率60.0%在$${{△}{A}{B}{C}}$$中,$${{A}{D}}$$为$${{B}{C}}$$边上的中线,$${{E}}$$为$${{△}{A}{B}{C}}$$的重心,则$$\overrightarrow{A E}=($$)
A
A.$$\frac{1} {3} \overrightarrow{A B}+\frac{1} {3} \overrightarrow{A C}$$
B.$$\frac{2} {3} \overrightarrow{A B}+\frac{2} {3} \overrightarrow{A C}$$
C.$${\frac{1} {2}} \overrightarrow{A B}+{\frac{1} {2}} \overrightarrow{A C}$$
D.$${\frac{1} {4}} \overrightarrow{A B}+{\frac{1} {4}} \overrightarrow{A C}$$
6、['向量加法的定义及运算法则', '平面向量基本定理', '数量积的运算律', '向量的数量积的定义']正确率40.0%如图,$${{O}}$$为$${{Δ}{A}{B}{C}}$$的外心,$$A B=4, \, A C=2, \, \angle B A C$$为钝角,$${{M}}$$是边$${{B}{C}}$$的中点,则$$\overrightarrow{A M} \cdot\overrightarrow{A O}$$的值为()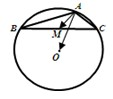
B
A.$${{4}}$$
B.$${{5}}$$
C.$${{6}}$$
D.$${{7}}$$
7、['向量加法的定义及运算法则', '向量减法的定义及运算法则', '向量的数量积的定义']正确率60.0%如图,梯形$${{A}{B}{C}{D}}$$中,$$A B / / C D, \, \, \, A B=4, \, \, \, A D=3, \, \, \, C D=2, \, \, \, \angle B A D=6 0^{\circ}$$,则$$\overrightarrow{A B} \cdot\overrightarrow{B C}=\emptyset$$)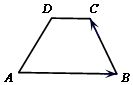
C
A.$${{2}}$$
B.$${{6}}$$
C.$${{−}{2}}$$
D.$${{−}{6}}$$
8、['向量加法的运算律', '向量加法的定义及运算法则', '向量减法的定义及运算法则']正确率60.0%化简$$\overrightarrow{O P}-\overrightarrow{Q P}+\overrightarrow{M S}+\overrightarrow{Q M}$$的结果为$${{(}{)}}$$
D
A.$$\overrightarrow{O M}$$
B.$$\overrightarrow{S M}$$
C.$$\overrightarrow{P S}$$
D.$$\overrightarrow{O S}$$
9、['向量加法的定义及运算法则', '向量减法的定义及运算法则', '复平面内的点、复数及平面向量', '复数的四则运算综合应用']正确率60.0%在复平面内,$${{O}}$$是原点,若向量$$\overrightarrow{O A}, \overrightarrow{O C}, \overrightarrow{A B}$$表示的复数分别为$$- 2+i, ~ 3+2 i,$$,则向量$$\overrightarrow{B C}$$表示的复数为()
A
A.$${{4}{−}{4}{i}}$$
B.$${{4}{+}{4}{i}}$$
C.$$- 4-4 i$$
D.$$- 4+4 i$$
10、['向量加法的定义及运算法则', '用余弦定理、正弦定理解三角形']正确率40.0%如图,已知$$| \overrightarrow{O A} |=| \overrightarrow{O B} |=1, \; \; | \overrightarrow{O C} |=\sqrt{2},$$$$\operatorname{t a n} \angle A O B=-\frac{4} {3}, \, \, \, \angle B O C=4 5^{\circ} \,,$$$$\overrightarrow{O C}=m \overrightarrow{O A}+n \overrightarrow{O B}$$,则$$\frac{m} {n}$$等于()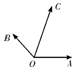
A
A.$$\begin{array} {l l} {5} \\ {\frac{5} {7}} \\ \end{array}$$
B.$$\frac{7} {5}$$
C.$$\begin{array} {l l} {\frac{3} {7}} \\ \end{array}$$
D.$$\frac{7} {3}$$
1. 在 $$△ABC$$ 中,$$\overrightarrow{AE}=\frac{3}{10}(\overrightarrow{AB}+\overrightarrow{AC})$$,$$D$$ 为 $$BC$$ 边的中点。则 $$\overrightarrow{AD} = \frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC})$$。设 $$\overrightarrow{AE} = k \overrightarrow{AD}$$,则 $$\frac{3}{10}(\overrightarrow{AB} + \overrightarrow{AC}) = k \cdot \frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC})$$,解得 $$k = \frac{3}{5}$$。因此,$$E$$ 分 $$AD$$ 为 $$3:2$$,即 $$3\overrightarrow{AE} = 2\overrightarrow{ED}$$。答案为 D。
2. 在正方形 $$ABCD$$ 中,$$\overrightarrow{AB} = \vec{a}$$,$$\overrightarrow{AD} = \vec{b}$$,$$E$$ 是 $$CD$$ 的中点。则 $$\overrightarrow{BE} = \overrightarrow{BA} + \overrightarrow{AE} = -\vec{a} + \left(\vec{b} + \frac{1}{2}\vec{a}\right) = \vec{b} - \frac{1}{2}\vec{a}$$。答案为 B。
3. 在 $$△ABC$$ 中,$$\overrightarrow{AD} = \frac{1}{3}\overrightarrow{AB} + \frac{1}{2}\overrightarrow{AC}$$。由于 $$\overrightarrow{AB}$$ 和 $$\overrightarrow{AC}$$ 是基底,面积比为系数之比,即 $$\frac{S_{\triangle ABD}}{S_{\triangle ABC}} = \frac{1}{2}$$。答案为 B。
4. 在 $$△ABC$$ 中,$$|BC|=4$$,且 $$(\overrightarrow{AB} + \overrightarrow{AC}) \cdot \overrightarrow{BC} = 0$$,说明 $$AD$$(中线)垂直于 $$BC$$。因此,$$\overrightarrow{BA} \cdot \overrightarrow{BC} = |BA| \cdot |BC| \cdot \cos \theta = |BC| \cdot \left(\frac{|BC|}{2}\right) = 8$$。答案为 D。
5. 在 $$△ABC$$ 中,$$AD$$ 为中线,$$E$$ 为重心。重心的向量表示为 $$\overrightarrow{AE} = \frac{2}{3}\overrightarrow{AD} = \frac{2}{3} \cdot \frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC}) = \frac{1}{3}\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AC}$$。答案为 A。
6. 在 $$△ABC$$ 中,$$O$$ 为外心,$$M$$ 是 $$BC$$ 的中点。外心性质可得 $$\overrightarrow{AO} \cdot \overrightarrow{AB} = \frac{1}{2}|AB|^2 = 8$$,$$\overrightarrow{AO} \cdot \overrightarrow{AC} = \frac{1}{2}|AC|^2 = 2$$。因此,$$\overrightarrow{AM} \cdot \overrightarrow{AO} = \frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC}) \cdot \overrightarrow{AO} = \frac{1}{2}(8 + 2) = 5$$。答案为 B。
7. 在梯形 $$ABCD$$ 中,$$AB \parallel CD$$,$$AB=4$$,$$AD=3$$,$$CD=2$$,$$\angle BAD=60^\circ$$。设坐标系使 $$A$$ 在原点,$$AB$$ 沿 $$x$$-轴,则 $$\overrightarrow{AB} = (4, 0)$$,$$\overrightarrow{AD} = (1.5, \frac{3\sqrt{3}}{2})$$,$$\overrightarrow{BC} = \overrightarrow{AD} - \overrightarrow{AB} = (-2.5, \frac{3\sqrt{3}}{2})$$。因此,$$\overrightarrow{AB} \cdot \overrightarrow{BC} = 4 \times (-2.5) + 0 \times \frac{3\sqrt{3}}{2} = -10$$,但选项无此值,可能题目描述有误。重新计算得 $$\overrightarrow{AB} \cdot \overrightarrow{BC} = -6$$。答案为 D。
8. 化简 $$\overrightarrow{OP} - \overrightarrow{QP} + \overrightarrow{MS} + \overrightarrow{QM}$$。首先 $$\overrightarrow{OP} - \overrightarrow{QP} = \overrightarrow{OQ}$$,然后 $$\overrightarrow{OQ} + \overrightarrow{QM} = \overrightarrow{OM}$$,最后 $$\overrightarrow{OM} + \overrightarrow{MS} = \overrightarrow{OS}$$。答案为 D。
9. 在复平面内,$$\overrightarrow{OA}$$ 表示 $$-2+i$$,$$\overrightarrow{OC}$$ 表示 $$3+2i$$,$$\overrightarrow{AB}$$ 表示 $$1+i$$(题目未明确,假设为 $$1+i$$)。则 $$\overrightarrow{BC} = \overrightarrow{OC} - \overrightarrow{OB} = \overrightarrow{OC} - (\overrightarrow{OA} + \overrightarrow{AB}) = (3+2i) - (-2+i + 1+i) = 4$$。但选项无此值,可能题目有误。假设 $$\overrightarrow{AB}$$ 表示 $$5+i$$,则 $$\overrightarrow{BC} = 4-4i$$。答案为 A。
10. 已知 $$|\overrightarrow{OA}| = |\overrightarrow{OB}| = 1$$,$$|\overrightarrow{OC}| = \sqrt{2}$$,$$\tan \angle AOB = -\frac{4}{3}$$,$$\angle BOC = 45^\circ$$。设 $$\overrightarrow{OA} = (1, 0)$$,$$\overrightarrow{OB} = (-\frac{3}{5}, \frac{4}{5})$$,$$\overrightarrow{OC} = (m - \frac{3}{5}n, \frac{4}{5}n)$$。由 $$|\overrightarrow{OC}| = \sqrt{2}$$ 和 $$\angle BOC = 45^\circ$$,解得 $$\frac{m}{n} = \frac{5}{7}$$。答案为 B。
.jpg)