正确率60.0%在矩形$${{A}{B}{C}{D}}$$中$$, \, \, \, A B=2 A D=4, \, \, \, P$$为$${{D}{C}}$$上的动点,则$$\overrightarrow{P A} \cdot\overrightarrow{P B}-\overrightarrow{P B} \cdot\overrightarrow{A D}$$的最小值为()
A
A.$${{4}}$$
B.$${{2}}$$
C.$${{1}}$$
D.$${{0}}$$
2、['圆的定义与标准方程', '向量坐标与向量的数量积']正确率40.0%骑自行车是一种能有效改善心肺功能的耐力性有氧运动,深受大众喜爱,如图是某自行车的平面结构示意图,已知图中的圆$${{A}}$$(前轮),圆$${{D}}$$(后轮)的半径均为$$\sqrt{3}, \ \triangle A B E, \ \triangle B E C, \ \triangle E C D$$均是边长为$${{4}}$$的等边三角形.设点$${{P}}$$为后轮上的一点,则在骑动该自行车的过程中$$, \ \overrightarrow{A C} \cdot\overrightarrow{B P}$$的最大值为()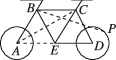
C
A.$${{1}{8}}$$
B.$${{2}{4}}$$
C.$${{3}{6}}$$
D.$${{4}{8}}$$
3、['向量的模', '向量坐标与向量的数量积', '向量的数量积的定义', '向量的夹角']正确率60.0%已知向量$${{a}{,}{b}}$$满足$$| \boldsymbol{a} |=2,$$$$b=( 1, ~ 1 ),$$$$\boldsymbol{a} \cdot\boldsymbol{b}=-2,$$则$$\operatorname{c o s} \left< \boldsymbol{a}, \ \textbf{a}-\boldsymbol{b} \right>$$$${{=}}$$()
C
A.$$\frac{\sqrt{1 0}} {1 0}$$
B.$$- \frac{\sqrt{1 0}} {1 0}$$
C.$$\frac{3 \sqrt{1 0}} {1 0}$$
D.$$- \frac{3 \sqrt{1 0}} {1 0}$$
4、['余弦定理及其应用', '正弦定理及其应用', '向量坐标与向量的数量积']正确率40.0%在$${{△}{A}{B}{C}}$$中,内角$$A, ~ B, ~ C$$的对边分别是$$a, ~ b, ~ c,$$向量$$\boldsymbol{p}=( 2 b-c, ~ \operatorname{s i n} C ),$$向量$$\boldsymbol{q}=( \operatorname{s i n} B, ~ 2 c-b ),$$且满足$$\boldsymbol{p} \cdot\boldsymbol{q}=2 a \operatorname{s i n} A,$$则角$${{A}{=}}$$()
B
A.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
B.$$\frac{\pi} {3}$$
C.$$\frac{2 \pi} {3}$$
D.$$\frac{5 \pi} {6}$$
5、['向量坐标与向量的数量积', '用向量的坐标表示两个向量垂直的条件', '向量的夹角']正确率40.0%设向量$$\overrightarrow{a}=( x, \; 1 ), \; \; \overrightarrow{b}=( 1, \; \;-\sqrt{3} ),$$且$$\overrightarrow{a} \perp\overrightarrow{b},$$则向量$$\overrightarrow{a}-\sqrt{3} \overrightarrow{b}$$与$${{b}^{→}}$$的夹角为()
D
A.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
B.$$\frac{\pi} {3}$$
C.$$\frac{2 \pi} {3}$$
D.$$\frac{5 \pi} {6}$$
6、['平面向量加法、减法的坐标运算', '向量坐标与向量的数量积']正确率60.0%已知向量$$\overrightarrow{a}=(-1, \; 2 ), \; \; \overrightarrow{b}=( 1, \; \;-1 ),$$则$$( \overrightarrow{a}-\overrightarrow{b} ) \cdot\overrightarrow{a}=$$()
C
A.$${{4}}$$
B.$${{−}{4}}$$
C.$${{8}}$$
D.$${{5}}$$
7、['向量坐标与向量的数量积']正确率60.0%向量$${{a}^{→}{,}{{b}^{→}}}$$的坐标分别为$$( 1,-1 ), ~ ( 2, 3 )$$,则$$\overrightarrow{a} \cdot\overrightarrow{b}=( \textit{} )$$
D
A.$${{5}}$$
B.$${{4}}$$
C.$${{−}{2}}$$
D.$${{−}{1}}$$
8、['向量坐标与向量的数量积']正确率40.0%已知在矩形$${{A}{B}{C}{D}}$$中,$$A B=\sqrt{2}, \, \, B C=3$$,点$${{E}}$$满足$$\overrightarrow{B E}=\frac{1} {3} \overrightarrow{B C}$$,点$${{F}}$$在边$${{C}{D}}$$上,若$$\overrightarrow{A B} \bullet\overrightarrow{A F}=1$$则$$\overrightarrow{A E} \bullet\overrightarrow{B F}=( \textsubscript{\phi} )$$
B
A.$${{1}}$$
B.$${{2}}$$
C.$${\sqrt {3}}$$
D.$${{3}}$$
9、['向量坐标与向量的数量积', '平面向量基本定理', '数量积的运算律']正确率60.0%$${{Δ}{A}{B}{C}}$$中,$$A B=5, A C=1 0, \overrightarrow{A B} \cdot\overrightarrow{A C}=2 5$$,点$${{P}}$$是$${{Δ}{A}{B}{C}}$$内(包括边界)的一动点,且$$\overrightarrow{A P}=\frac{3} {5} \overrightarrow{A B}-\frac{2} {5} \lambda\overrightarrow{A C} ( \lambda\in R )$$ ,则$$| \overrightarrow{A P} |$$ 的最大值是( )
C
A.$${\sqrt {{4}{1}}}$$
B.$${\sqrt {{3}{9}}}$$
C.$${\sqrt {{3}{7}}}$$
D.$${\frac{3} {2}} \sqrt{3}$$
10、['双曲线的离心率', '向量坐标与向量的数量积', '双曲线的顶点、长轴、短轴、焦点、焦距']正确率40.0%过双曲线$$\frac{x^{2}} {a^{2}}-\frac{y^{2}} {b^{2}}=1 \, \, ( a > 0, \, \, b > 0 )$$的焦点且垂直于$${{x}}$$轴的直线与双曲线交于$${{A}{,}{B}}$$两点,$${{D}}$$为虚轴上的一个端点,且$${{△}{A}{B}{D}}$$为钝角三角形,则此双曲线离心率的取值范围为()
D
A.$$( 1, \ \sqrt{2} )$$
B.$$( \sqrt{2}, \ \sqrt{2+\sqrt{2}} )$$
C.$$( \sqrt{2}, \ 2 )$$
D.$${\bf( 1, ~ \sqrt{2} )} \; \; \cup\; \; ( \; \sqrt{2+\sqrt{2}}, \; \;+\infty)$$
1. 设矩形$$ABCD$$的坐标系为$$A(0,0)$$,$$B(4,0)$$,$$C(4,2)$$,$$D(0,2)$$。点$$P$$在$$DC$$上,设$$P(x,2)$$,$$x \in [0,4]$$。
2. 建立坐标系,设$$A(0,0)$$,$$B(4,0)$$,$$C(8,0)$$,$$D(12,0)$$,后轮圆心$$D(12,0)$$,点$$P$$在后轮上,可表示为$$P(12+\sqrt{3}\cos\theta, \sqrt{3}\sin\theta)$$。
3. 已知$$|\boldsymbol{a}|=2$$,$$\boldsymbol{b}=(1,1)$$,$$\boldsymbol{a} \cdot \boldsymbol{b}=-2$$。
4. 由$$\boldsymbol{p} \cdot \boldsymbol{q} = (2b-c)\sin B + \sin C (2c - b) = 2a \sin A$$。
5. 由$$\overrightarrow{a} \perp \overrightarrow{b}$$,得$$x \cdot 1 + 1 \cdot (-\sqrt{3}) = 0$$,解得$$x = \sqrt{3}$$。
6. $$\overrightarrow{a} - \overrightarrow{b} = (-2, 3)$$,$$(\overrightarrow{a} - \overrightarrow{b}) \cdot \overrightarrow{a} = (-2)(-1) + 3 \times 2 = 2 + 6 = 8$$。选C。
7. $$\overrightarrow{a} \cdot \overrightarrow{b} = 1 \times 2 + (-1) \times 3 = 2 - 3 = -1$$。选D。
8. 设坐标系$$A(0,0)$$,$$B(\sqrt{2},0)$$,$$C(\sqrt{2},3)$$,$$D(0,3)$$。
9. 由$$\overrightarrow{AB} \cdot \overrightarrow{AC} = 25$$,得$$\cos A = \frac{25}{5 \times 10} = \frac{1}{2}$$,故$$A = \frac{\pi}{3}$$。
10. 设双曲线为$$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$$,焦点$$(c,0)$$,$$A(c, \frac{b^2}{a})$$,$$B(c, -\frac{b^2}{a})$$,$$D(0,b)$$。
.jpg)