平面向量基本定理-6.3 平面向量基本定理及坐标表示知识点专题进阶自测题答案-北京市等高二数学必修,平均正确率52.0%

正确率80.0%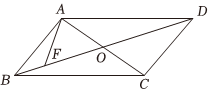如图所示，$${{F}}$$为平行四边形$${{A}{B}{C}{D}}$$对角线$${{B}{D}}$$上一点，$${{A}{C}}$$，$${{B}{D}}$$交于点$${{O}}$$，$$\overrightarrow{B F}=\frac{1} {3} \overrightarrow{F O}$$，若$$\overrightarrow{A F}=x \overrightarrow{A B}+y \overrightarrow{B C}$$，则$$x y=( \begin{array} {c} {} \\ \end{array} )$$

A.$$\frac{3} {1 6}$$

B.$$- \frac{3} {1 6}$$

C.$$\frac{7} {6 4}$$

D.$$- \frac{7} {6 4}$$

正确率19.999999999999996%在$${{△}{A}{B}{C}}$$中，点$${{P}}$$满足$$\overrightarrow{B P}=2 \overrightarrow{P C}，$$过点$${{P}}$$的直线与$$A B， \ A C$$所在直线分别交于点$${{M}{，}{N}}$$，若$$\overrightarrow{A M}=m \overrightarrow{A B}， \， \， \， \overrightarrow{A N}=n \overrightarrow{A C} ( m > 0， n > 0 ).$$则$${{m}{+}{2}{n}}$$的最小值为（）

D

A.$$\frac{8} {2}$$

B.$$\frac{1 0} {3}$$

C.$${{4}}$$

D.$${{3}}$$

正确率40.0%点$${_{D}}$$是$$\Delta A B C$$所在平面内的一点，且$$\overrightarrow{B D}=-2 \overrightarrow{D C}，$$，设$$\overrightarrow{A D}=\lambda\overrightarrow{A B}+\mu\overrightarrow{A C}，$$，则$$\lambda-\mu=~ ($$）

A

A.

B.$$-1$$

C.$${_{1}}$$

D.$${_{3}}$$

正确率60.0%三角形$${{A}{B}{C}}$$中，$$\overrightarrow{B D}=2 \overrightarrow{D C}$$，若$$\overrightarrow{A D}=\lambda\overrightarrow{A B}+\mu\overrightarrow{A C}，$$则$${{λ}{+}{μ}{=}}$$

D

A.$$\frac{4} {3}$$

B.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$

C.$${{2}}$$

D.$${{1}}$$

正确率60.0%在$${{△}{A}{B}{C}}$$中，$${{A}{D}}$$为$${{B}{C}}$$边上的中线，$${{E}}$$为$${{△}{A}{B}{C}}$$的重心，则$$\overrightarrow{A E}=($$）

A

A.$$\frac{1} {3} \overrightarrow{A B}+\frac{1} {3} \overrightarrow{A C}$$

B.$$\frac{2} {3} \overrightarrow{A B}+\frac{2} {3} \overrightarrow{A C}$$

C.$${\frac{1} {2}} \overrightarrow{A B}+{\frac{1} {2}} \overrightarrow{A C}$$

D.$${\frac{1} {4}} \overrightarrow{A B}+{\frac{1} {4}} \overrightarrow{A C}$$

正确率60.0%$${{D}}$$是$${{Δ}{A}{B}{C}}$$边$${{B}{C}}$$上的中点，则$$\overrightarrow{A D}=($$）

A

A.$${\frac{1} {2}} \overrightarrow{A B}+{\frac{1} {2}} \overrightarrow{A C}$$

B.$${\frac{1} {2}} \overrightarrow{A B}-{\frac{1} {2}} \overrightarrow{A C}$$

C.$$- \frac{1} {2} \overrightarrow{A B}+\frac{1} {2} \overrightarrow{A C}$$

D.$$- {\frac{1} {2}} \overrightarrow{A B}-{\frac{1} {2}} \overrightarrow{A C}$$

正确率40.0%在$${{△}{A}{B}{C}}$$中，$$\overrightarrow{B D}=2 \overrightarrow{D C}$$，则$$\overrightarrow{A D}=$$（）

B

A.$$\frac{1} {3} \overrightarrow{A B}-\frac{2} {3} \overrightarrow{A C}$$

B.$$\frac{1} {3} \overrightarrow{A B}+\frac{2} {3} \overrightarrow{A C}$$

C.$$\frac2 3 \overrightarrow{A B}-\frac1 3 \overrightarrow{A C}$$

D.$$\frac2 3 \overrightarrow{A B}+\frac1 3 \overrightarrow{A C}$$

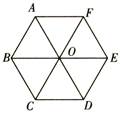
正确率80.0%如图所示，点$${{O}}$$为正六边形$$A B C D E F$$的中心，则可作为基底的一对向量是$${{(}{)}}$$

B

A.$$\overrightarrow{O A}$$，$$\overrightarrow{B C}$$

B.$$\overrightarrow{O A}$$，$$\overrightarrow{C D}$$

C.$$\overrightarrow{A B}$$，$$\overrightarrow{C F}$$

D.$$\overrightarrow{A B}$$，$$\overrightarrow{D E}$$

正确率0.0%已知：$$| \overrightarrow{O A} |=1$$，$$| \overrightarrow{O B} |=\sqrt{3}$$，$$\overrightarrow{O A} \cdot\overrightarrow{O B}=0$$，点$${{C}}$$在$${{∠}{A}{O}{B}}$$内，且$$\overrightarrow{O C}$$与$$\overrightarrow{O A}$$的夹角为$${{3}{0}{°}}$$，设$$\overrightarrow{O C}=m \overrightarrow{O A}+n \overrightarrow{O B} ( m， n \in R )$$，则$$\frac{m} {n}$$的值为$${{(}{)}}$$

C

A.$${{2}}$$

B.$$\frac{5} {2}$$

C.$${{3}}$$

D.$${{4}}$$

正确率80.0%已知点$${{G}}$$是$${{△}{A}{B}{C}}$$的重心，过点$${{G}}$$作直线分别与$${{A}{B}}$$，$${{A}{C}}$$两边交于$${{M}}$$，$${{N}}$$两点$${{(}}$$点$${{M}}$$，$${{N}}$$与点$${{B}}$$，$${{C}}$$不重合$${{)}}$$，设$$\overrightarrow{A B}=x \overrightarrow{A M}$$，$$\overrightarrow{A C}=y \overrightarrow{A N}$$，则$$\frac{1} {2 x-1}+\frac{1} {2 y-1}$$的最小值为$${{(}{)}}$$

A.$${{1}}$$

B.$$\frac{1+\sqrt2} {2}$$

C.$${{2}}$$

D.$${{1}{+}{2}{\sqrt {2}}}$$

设 $$O$$ 为平行四边形对角线交点，则 $$\overrightarrow{FO} = \frac{3}{4}\overrightarrow{BO}$$。由 $$\overrightarrow{AF} = \overrightarrow{AO} + \overrightarrow{OF} = \frac{1}{2}\overrightarrow{AC} - \frac{3}{4}\overrightarrow{BD}$$。将 $$\overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{BC}$$ 和 $$\overrightarrow{BD} = \overrightarrow{BC} - \overrightarrow{AB}$$ 代入，整理得 $$\overrightarrow{AF} = \frac{7}{8}\overrightarrow{AB} + \frac{1}{8}\overrightarrow{BC}$$。因此 $$x = \frac{7}{8}$$，$$y = \frac{1}{8}$$，$$xy = \frac{7}{64}$$。

正确答案：$$C$$

由 $$\overrightarrow{BP} = 2\overrightarrow{PC}$$，得 $$\overrightarrow{AP} = \frac{1}{3}\overrightarrow{AB} + \frac{2}{3}\overrightarrow{AC}$$。设直线 $$MN$$ 过 $$P$$，则 $$\overrightarrow{AP} = \frac{1}{m}\overrightarrow{AM} + \frac{1}{n}\overrightarrow{AN}$$。代入条件得 $$\frac{1}{m} + \frac{2}{n} = 1$$。利用不等式求 $$m + 2n$$ 的最小值，得 $$m + 2n \geq 4$$。

正确答案：$$C$$

由 $$\overrightarrow{BD} = -2\overrightarrow{DC}$$，得 $$\overrightarrow{AD} = \frac{1}{3}\overrightarrow{AB} + \frac{2}{3}\overrightarrow{AC}$$。因此 $$\lambda = \frac{1}{3}$$，$$\mu = \frac{2}{3}$$，$$\lambda - \mu = -1$$。

正确答案：$$B$$

由 $$\overrightarrow{BD} = 2\overrightarrow{DC}$$，得 $$\overrightarrow{AD} = \frac{1}{3}\overrightarrow{AB} + \frac{2}{3}\overrightarrow{AC}$$。因此 $$\lambda + \mu = 1$$。

正确答案：$$D$$

重心 $$E$$ 分中线 $$AD$$ 为 $$2:1$$，故 $$\overrightarrow{AE} = \frac{2}{3}\overrightarrow{AD}$$。又 $$\overrightarrow{AD} = \frac{1}{2}\overrightarrow{AB} + \frac{1}{2}\overrightarrow{AC}$$，因此 $$\overrightarrow{AE} = \frac{1}{3}\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AC}$$。

正确答案：$$A$$

$$D$$ 为 $$BC$$ 中点，故 $$\overrightarrow{AD} = \frac{1}{2}\overrightarrow{AB} + \frac{1}{2}\overrightarrow{AC}$$。

正确答案：$$A$$

由 $$\overrightarrow{BD} = 2\overrightarrow{DC}$$，得 $$\overrightarrow{AD} = \frac{1}{3}\overrightarrow{AB} + \frac{2}{3}\overrightarrow{AC}$$。

正确答案：$$B$$

基底需为不共线的向量。选项 $$C$$ 中 $$\overrightarrow{AB}$$ 与 $$\overrightarrow{CF}$$ 不共线，可作为基底。

正确答案：$$C$$

设坐标系使 $$\overrightarrow{OA}$$ 沿 $$x$$ 轴，$$\overrightarrow{OB}$$ 沿 $$y$$ 轴。由题意，$$\overrightarrow{OC} = (m, n\sqrt{3})$$，与 $$\overrightarrow{OA}$$ 夹角 $$30^\circ$$，故 $$\tan 30^\circ = \frac{n\sqrt{3}}{m}$$，解得 $$\frac{m}{n} = 3$$。

正确答案：$$C$$

重心 $$G$$ 满足 $$\overrightarrow{AG} = \frac{1}{3}\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AC}$$。设 $$\overrightarrow{AM} = \frac{1}{x}\overrightarrow{AB}$$，$$\overrightarrow{AN} = \frac{1}{y}\overrightarrow{AC}$$，由 $$G$$ 在 $$MN$$ 上得 $$\frac{1}{x} + \frac{1}{y} = 3$$。化简后利用不等式得最小值为 $$1 + 2\sqrt{2}$$。

正确答案：$$D$$