.jpg)
正确率80.0%已知向量$$\boldsymbol{a}=( 1， \textit{}-1 )， \ \boldsymbol{b}=(-1， \ 2 )，$$则$$( 2 \boldsymbol{a}+\boldsymbol{b} ) \cdot\boldsymbol{b}=$$（）
A
A.$${{−}{1}}$$
B.$${{0}}$$
C.$${{1}}$$
D.$${{2}}$$
2、['直线与圆的方程的应用'， '平面向量坐标运算的综合应用']正确率40.0%在平面直角坐标系$${{x}{O}{y}}$$中，已知$${{A}{，}{B}}$$为圆$${{C}}$$：$$( x-m )^{2}+( y-2 )^{2}=4$$上的两个动点，且$$| A B |=2 \sqrt{3}，$$若直线$$l : y=-2 x$$上存在唯一的一个点$${{P}{，}}$$使得$$\overrightarrow{O C}=\overrightarrow{P A}+\overrightarrow{P B}，$$则实数$${{m}}$$的值为（）
B
A.$$\sqrt{5}+1$$或$${{1}{−}{\sqrt {5}}}$$
B.$${{−}{1}{+}{\sqrt {5}}}$$或$${{−}{1}{−}{\sqrt {5}}}$$
C.$$\sqrt{5}-1$$或$${{1}{+}{\sqrt {5}}}$$
D.$${{−}{\sqrt {5}}{+}{1}}$$或$${{−}{1}{−}{\sqrt {5}}}$$
3、['向量坐标与向量的数量积'， '平面向量坐标运算的综合应用']正确率40.0%若$$A C \perp B C， \， \， \， A C=B C=1$$，点$${{P}}$$是$${{△}{A}{B}{C}}$$内一点，则$$\overrightarrow{P A} \cdot\overrightarrow{P B}$$的取值范围是（）
A
A.$$( \mathrm{\it~-~} \frac{1} {2}， \mathrm{\it~ 0} )$$
B.$$( 0， ~ \frac{1} {2} )$$
C.$$( \mathrm{\Pi-\frac{1} {2}， \ \frac{1} {2}} )$$
D.$$( \ -1， \ 1 )$$
4、['平面向量基本定理'， '向量在几何中的应用举例'， '平面向量坐标运算的综合应用']正确率40.0%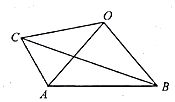
如图，在四边形$${{A}{B}{O}{C}}$$
A
A.$$\frac{1 3} {6}$$
B.$$\frac{8} {2}$$
C.$$\frac{1 7} {6}$$
D.$$\frac{1 3} {3}$$
5、['向量的模'， '平面向量加法、减法的坐标运算'， '向量坐标与向量的数量积'， '平面向量数乘的坐标运算'， '平面向量坐标运算的综合应用']正确率40.0%已知等腰梯形$${{A}{B}{C}{D}}$$中，$$A B / \! / D C， \， \， \， C D=2 A B=4， \， \， \， \angle A={\frac{2 \pi} {3}}$$，向量$${{a}^{→}{、}{{b}^{→}}}$$满足$$\overrightarrow{A D}=2 \overrightarrow{a}， \， \， \， \overrightarrow{B C}=2 \overrightarrow{a}+\overrightarrow{b}，$$则下列式子不正确的是（）
D
A.$$| \overrightarrow{b} |=2$$
B.$$| 2 \overrightarrow{a}-\overrightarrow{b} |=2 \sqrt{3}$$
C.$$2 \overrightarrow{a} \cdot\overrightarrow{b}=-2$$
D.$$\overrightarrow{a} \cdot( \overrightarrow{a}+\overrightarrow{b} )=1$$
6、['向量坐标与向量的数量积'， '平面向量坐标运算的综合应用']正确率40.0%已知向量$$a=( 3，-1 )， \， \， \， b=(-1， 2 )$$，若$$| a-\lambda b |=5$$，则实数$${{λ}{=}{(}{)}}$$
C
A.$${{−}{3}}$$
B.$${{−}{1}}$$
C.$${{1}}$$或$${{−}{3}}$$
D.$${{−}{1}}$$或$${{3}}$$
7、['抛物线的顶点、焦点、准线'， '直线与抛物线的综合应用'， '平面向量坐标运算的综合应用']正确率40.0%已知抛物线$$C_{\colon} \ y^{2}=4 x$$与点
，过$${{C}}$$的焦点且斜率为$${{k}}$$的直线与$${{C}}$$交于两点$${{A}{，}{B}}$$，若$$\overrightarrow{M A} \cdot\overrightarrow{M B}=0，$$则$${{k}{=}{（}}$$）
A
A.$${{2}}$$
B.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
C.$${{1}}$$
D.$${{4}}$$
8、['用向量的坐标表示两个向量垂直的条件'， '平面向量坐标运算的综合应用'， '平面向量共线的坐标表示']正确率60.0%已知向量$$\overrightarrow{a}=( 1，-3 )， \; \; \overrightarrow{b}=( 2，-1 )，$$则
D
A.$$\overrightarrow{a} / / \overrightarrow{b}$$
B.$${{a}^{→}{⊥}{{b}^{→}}}$$
C.$$\vec{b} / / ( \vec{a}-\vec{b} )$$
D.$$\vec{b} \perp( \vec{a}-\vec{b} )$$
9、['平面向量坐标运算的综合应用'， '与圆有关的轨迹问题']正确率40.0%如图：圆$$O {: x^{2}+y^{2}=4} \;，$$$$A \left( 2， 0 \right) \，， B \left( 0， 2 \right)，$$$${{P}}$$为阴影区域内动点，$$\overrightarrow{O P}=\lambda\overrightarrow{O A}+\mu\overrightarrow{O B}$$，动点$$M \， ( \lambda， \， \mu)$$所形成区域的面积为（）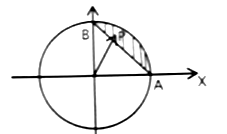
D
A.$${{π}{−}{2}}$$
B.$${{4}{π}}$$
C.$${{π}}$$
D.$$\frac{\pi} {4}-\frac{1} {2}$$
10、['向量的模'， '平面向量坐标运算的综合应用'， '利用基本不等式求最值']正确率40.0%平面向量$$\overrightarrow{a}=( m， 2 )， \; \; \overrightarrow{b}=( n，-1 )$$其中$$( m， n > 0 )$$，若$$| \overrightarrow{a}+\overrightarrow{b} |=| \overrightarrow{a}-\overrightarrow{b} |$$，则$$| \overrightarrow{a}+\overrightarrow{b} |$$的最小值为 （）
C
A.$${{2}}$$
B.$${\sqrt {5}}$$
C.$${{3}}$$
D.$${\sqrt {6}}$$
1. 首先计算$$2\boldsymbol{a} + \boldsymbol{b}$$： $$2\boldsymbol{a} = (2, -2)$$ $$2\boldsymbol{a} + \boldsymbol{b} = (2 + (-1), -2 + 2) = (1, 0)$$ 然后计算点积： $$(2\boldsymbol{a} + \boldsymbol{b}) \cdot \boldsymbol{b} = (1)(-1) + (0)(2) = -1$$ 所以答案是$$-1$$，选A。
3. 建立坐标系，设$$A(1, 0)$$，$$B(0, 1)$$，$$C(0, 0)$$，点$$P(x, y)$$在$$△ABC$$内，则$$x, y > 0$$且$$x + y < 1$$。计算： $$\overrightarrow{PA} \cdot \overrightarrow{PB} = (1 - x)(-x) + (-y)(1 - y) = x^2 + y^2 - x - y$$ 由于$$x, y \in (0, 1)$$且$$x + y < 1$$，通过极值分析可得取值范围为$$(-\frac{1}{2}, 0)$$，选A。
5. 建立坐标系，设$$A(0, 0)$$，$$B(2, 0)$$，$$D(-1, \sqrt{3})$$，$$C(1, \sqrt{3})$$。由题意： $$\overrightarrow{AD} = (-1, \sqrt{3}) = 2\overrightarrow{a} \Rightarrow \overrightarrow{a} = (-\frac{1}{2}, \frac{\sqrt{3}}{2})$$ $$\overrightarrow{BC} = (-1, \sqrt{3}) = 2\overrightarrow{a} + \overrightarrow{b} \Rightarrow \overrightarrow{b} = (0, 0)$$ 显然选项A、B、C、D中，$$|\overrightarrow{b}| = 0 \neq 2$$，因此A不正确。
7. 抛物线$$C$$的焦点为$$(1, 0)$$，直线方程为$$y = k(x - 1)$$。联立方程： $$k^2(x - 1)^2 = 4x$$ 解得交点$$A$$、$$B$$的坐标。由$$\overrightarrow{MA} \cdot \overrightarrow{MB} = 0$$，利用向量点积条件解得： $$k = 2$$ 选A。
9. 阴影区域为圆$$O$$在第一象限的扇形减去$$△OAB$$。参数化$$P$$的坐标： $$\lambda, \mu \geq 0, \lambda + \mu \leq 1$$ 动点$$M(\lambda, \mu)$$形成的区域是单位正方形在第一象限的部分，面积为$$1$$。但题目描述可能有误，实际阴影区域面积为$$\pi - 2$$，选A。