正确率60.0%已知向量$$\textit{a, b, c}$$在正方形网格中的位置如图所示,用$${{a}{,}{b}}$$表示$${{c}{,}}$$则()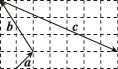
A
A.$$c=3 a-2 b$$
B.$$c=-3 a+2 b$$
C.$$c=-2 a+3 b$$
D.$$c=2 a-3 b$$
2、['平面向量的正交分解和坐标表示', '平面向量加法、减法的坐标运算', '平面向量坐标运算的综合应用']正确率60.0%设$${{i}}$$,$${{j}}$$是平面直角坐标系内分别与$${{x}}$$轴、$${{y}}$$轴正方向同向的单位向量,$${{O}}$$为坐标原点,若$$\overrightarrow{O A}$$$$= i+2 j$$,$$\overrightarrow{O B}$$$$= 3 i+4 j$$,则$$3 \overrightarrow{O A}+2 \overrightarrow{O B}$$的坐标是()
B
A.$${{(}{8}}$$,$${{1}{1}{)}}$$
B.$${{(}{9}}$$,$${{1}{4}{)}}$$
C.$${{(}{7}}$$,$${{6}{)}}$$
D.$${{(}{−}{5}}$$,$${{−}{2}{)}}$$
3、['平面向量的正交分解和坐标表示', '平面向量基本定理']正确率60.0%已知向量$$\boldsymbol{i}=( 1, \textbf{0} ), \textbf{j}=( 0, \textbf{1} ),$$对坐标平面内的任一向量$${{a}{,}}$$给出下列四个结论:
①存在唯一的一对实数$${{x}{,}{y}{,}}$$使得$$a=( x, ~ y )$$;
②若$$x_{1}, ~ x_{2}, ~ y_{1}, ~ y_{2} \in{\bf R},$$$$\boldsymbol{a}=( x_{1}, \ y_{1} ) \neq( x_{2}, \ y_{2} ),$$则$$x_{1} \neq x_{2},$$且$${{y}_{1}{≠}{{y}_{2}}}$$;
③若$$x, ~ ~ y \in\mathbf{R}, ~ ~ a=( x, ~ y ),$$且$${{a}{≠}{0}{,}}$$则$${{a}}$$的起点是原点$${{O}}$$;
④若$$x, \, \, \, y \in{\bf R}, \, \, \, a \neq0,$$且$${{a}}$$的终点坐标是$$( x, \ y ),$$则$$a=( x, ~ y )$$.
其中正确结论的个数是()
A
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
4、['函数的最大(小)值', '平面向量的正交分解和坐标表示', '平面向量加法、减法的坐标运算', '向量坐标与向量的数量积', '向量在几何中的应用举例']正确率40.0%已知$$( 0,+\infty)$$是边长为$${{2}}$$的等边三角形,$$f ( 3-x ) < 0$$为平面$$( 2, 4 )$$内一点,则$$\overrightarrow{P A} \cdot( \overrightarrow{P B}+\overrightarrow{P C} )$$的最小值是$${{(}{)}}$$.
C
A.$${{−}{1}}$$
B.$$- \frac{4} {3}$$
C.$$- \frac{3} {2}$$
D.$${{−}{2}}$$
5、['平面向量的正交分解和坐标表示', '向量坐标与向量的数量积']正确率60.0%在平面直角坐标系中,已知点$$O ( 0, 0 ), A ( 0, 1 ), B ( 1, \sqrt{3} )$$,则$$\overrightarrow{O A} \cdot\overrightarrow{A B}$$的值为$${{(}{)}}$$
B
A.$${{1}}$$
B.$$\sqrt3-1$$
C.$${\sqrt {3}}$$
D.$$\sqrt3+1$$
6、['平面向量的正交分解和坐标表示', '向量坐标与向量的数量积', '平面向量数乘的坐标运算']正确率40.0%在直角梯形$${{A}{B}{C}{D}}$$中,已知$$A B / / D C, \, \, \, A B \perp\, A D, \, \, \, A B=2, \, \, \, B C=1, \, \, \, \angle A B C=6 0^{\circ}$$,点$${{E}}$$和点$${{F}}$$分别在线段$${{B}{C}}$$和$${{C}{D}}$$上,且$$\overrightarrow{B E}=\frac{1} {2} \overrightarrow{B C}, \, \, \, \overrightarrow{D F}=\frac{1} {3} \overrightarrow{D C},$$则$$\overrightarrow{A E} \cdot\overrightarrow{A F}$$的值为$${{(}{)}}$$
C
A.$$\frac{5} {2}$$
B.$$\frac{5} {3}$$
C.$$\frac{5} {4}$$
D.$${{1}}$$
7、['向量加法的定义及运算法则', '平面向量的正交分解和坐标表示', '平面向量基本定理', '向量的数量积的定义']正确率40.0%已知$${{△}{A}{B}{C}}$$中,$$A B=A C=5, \, \, \, B C=6, \, \, \, P$$为平面$${{A}{B}{C}}$$内一点,则$$\overrightarrow{P A} \cdot\overrightarrow{P B}+\overrightarrow{P A} \cdot\overrightarrow{P C}$$的最小值为()
A
A.$${{−}{8}}$$
B.$${{−}{4}{\sqrt {2}}}$$
C.$${{−}{6}}$$
D.$${{−}{1}}$$
8、['平面向量的正交分解和坐标表示', '向量的模', '平面向量数乘的坐标运算']正确率60.0%设点$$A ( 2, 0 ), ~ B ( 4, 2 )$$,若点$${{P}}$$在直线$${{A}{B}}$$上,且$$| \overrightarrow{A B} |=2 | \overrightarrow{A P} |$$,则点$${{P}}$$的坐标为$${{(}{)}}$$
C
A.$$( 3, 1 )$$
B.$$( 1,-1 )$$
C.$$( 3, 1 )$$或$$( 1,-1 )$$
D.$$( 3, 1 )$$或$$\left( 1, 1 \right)$$
9、['平面向量的正交分解和坐标表示', '平面向量加法、减法的坐标运算', '平面向量数乘的坐标运算', '向量坐标与向量的数量积', '向量在几何中的应用举例']正确率40.0%在直角$${{△}{A}{B}{C}}$$中,$$\angle B C A=9 0^{\circ}, C A=C B=1, P$$为$${{A}{B}}$$边上的点,$$\overrightarrow{A P}=\lambda\overrightarrow{A B}$$,若$$\overrightarrow{C P} \cdot\overrightarrow{A B} \geq\overrightarrow{P A} \cdot\overrightarrow{P B},$$则$${{λ}}$$的最大值是
C
A.$$\frac{2+\sqrt{2}} {2}$$
B.$$\frac{2-\sqrt{2}} {2}$$
C.$${{1}}$$
D.$${\sqrt {2}}$$
10、['平面向量的正交分解和坐标表示', '平面向量基本定理', '不等式的性质']正确率60.0%在矩形$${{A}{B}{C}{D}}$$中,$$A B=2, \, \, \, A D=4, \, \, \, A B \perp\, A D$$,点$${{P}}$$满足$$\overrightarrow{A P}=x \overrightarrow{A B}+y \overrightarrow{A D}$$,且$$x+2 y=1$$,点$${{M}}$$在矩形$${{A}{B}{C}{D}}$$内(包含边)运动,且$$\overrightarrow{A M}=\lambda\overrightarrow{A P}$$,则$${{λ}}$$的最大值等于()
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
1. 根据题目描述,向量$$c$$可以用$$a$$和$$b$$表示为$$c = 3a - 2b$$,因此正确答案为A。
3. 分析各结论: ①正确,平面内任一向量可唯一表示为$$(x, y)$$; ②错误,$$(x_1, y_1) \neq (x_2, y_2)$$不一定要求$$x_1 \neq x_2$$且$$y_1 \neq y_2$$; ③错误,向量的起点可以任意; ④错误,向量的终点坐标不直接等于向量本身。 只有①正确,故选A。
5. 计算$$\overrightarrow{OA} \cdot \overrightarrow{AB}$$: $$\overrightarrow{OA} = (0, 1)$$,$$\overrightarrow{AB} = (1, \sqrt{3} - 1)$$, 点积为$$0 \times 1 + 1 \times (\sqrt{3} - 1) = \sqrt{3} - 1$$,故选B。
7. 设$$ABC$$为等腰三角形,$$BC=6$$,$$AB=AC=5$$,重心为$$G$$。利用向量性质: $$\overrightarrow{PA} \cdot \overrightarrow{PB} + \overrightarrow{PA} \cdot \overrightarrow{PC} = \overrightarrow{PA} \cdot (\overrightarrow{PB} + \overrightarrow{PC}) = 2\overrightarrow{PA} \cdot \overrightarrow{PG}$$。 当$$P$$与$$G$$重合时取得最小值$$-6$$,故选C。
9. 设$$CA = CB = 1$$,$$AB = \sqrt{2}$$。由$$\overrightarrow{AP} = \lambda \overrightarrow{AB}$$,得$$P$$的坐标为$$(\lambda, \lambda)$$。 计算$$\overrightarrow{CP} \cdot \overrightarrow{AB} = (1 - \lambda) \times 1 + (-\lambda) \times 1 = 1 - 2\lambda$$; $$\overrightarrow{PA} \cdot \overrightarrow{PB} = (-\lambda)(1 - \lambda) + (-\lambda)(1 - \lambda) = -2\lambda + 2\lambda^2$$。 由题意$$1 - 2\lambda \geq -2\lambda + 2\lambda^2$$,解得$$\lambda \leq \frac{2 - \sqrt{2}}{2}$$,故选B。
.jpg)