正确率60.0%已知向量$$\overrightarrow{A B}=( 2, \ 1 ),$$点$$C (-1, ~ 0 ), ~ D ( 4, ~ 5 ),$$则向量$$\overrightarrow{A B}$$在$$\overrightarrow{C D}$$方向上的投影为()
C
A.$$- \frac{3 \sqrt2} 2$$
B.$${{−}{3}{\sqrt {5}}}$$
C.$$\frac{3 \sqrt2} {2}$$
D.$${{3}{\sqrt {5}}}$$
2、['向量的模', '数量积的运算律', '向量的数量积的定义', '投影的数量']正确率40.0%已知平面向量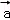 ,
,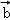 满足
满足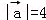 ,
,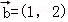 ,
,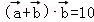 则向量
则向量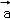 在向量
在向量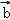 方向上的投影为$${{(}{)}}$$
方向上的投影为$${{(}{)}}$$
D
A.$${{2}}$$
B.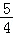
C.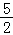
D.
正确率40.0%若空间向量$${{{e}_{1}}^{→}{,}{{{e}_{2}}^{→}}}$$满足$$| \vec{e}_{1} |=| 2 \vec{e}_{1}+\vec{e}_{2} |=3,$$则$${{{e}_{1}}^{→}}$$在$${{{e}_{2}}^{→}}$$方向上投影的最大值是()
C
A.$${{3}}$$
B.$${{0}}$$
C.$$- \frac{3 \sqrt{3}} {2}$$
D.$$- \frac{3} {2}$$
4、['向量坐标与向量的数量积', '投影的数量']正确率60.0%已知点$$A ~ ( \textbf{1}, \textbf{2} ) ~, \textbf{B} ~ ( \textbf{3}, \textbf{-1} )$$,则$$\overrightarrow{A B}$$在$${{y}}$$轴正方向上的投影是()
D
A.$${{3}}$$
B.$${{2}}$$
C.$${{−}{2}}$$
D.$${{−}{3}}$$
5、['数量积的性质', '数量积的运算律', '向量的数量积的定义', '投影向量(投影)', '投影的数量']正确率40.0%已知$$| \overrightarrow{a} |=2, \, \, | \overrightarrow{b} |=3, \, \, | \overrightarrow{a}-\overrightarrow{b} |=\sqrt{7}$$,则$${{a}^{→}}$$在$${{b}^{→}}$$方向的射影是$${{(}{)}}$$
A
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
6、['向量的模', '向量垂直', '向量的数量积的定义', '投影的数量']正确率60.0%已知向量$${{a}^{→}{,}{{b}^{→}}}$$满足$$| \overrightarrow{a} |=2, ~ ~ | \overrightarrow{b} |=\sqrt{2}$$,且$$\overrightarrow{a} \perp( \overrightarrow{a}+2 \overrightarrow{b} ),$$则$${{b}^{→}}$$在$${{a}^{→}}$$方向上的投影为()
B
A.$${{1}}$$
B.$${{−}{1}}$$
C.$${\sqrt {2}}$$
D.$${{−}{\sqrt {2}}}$$
7、['数量积的性质', '数量积的运算律', '向量的数量积的定义', '投影的数量']正确率40.0%若平面向量$${{{e}_{1}}^{→}{,}{{{e}_{2}}^{→}}}$$满足$$| \overrightarrow{e_{1}} |=| 3 \overrightarrow{e_{1}}+\overrightarrow{e_{2}} |=2$$,则$${{{e}_{1}}^{→}}$$在$${{{e}_{2}}^{→}}$$方向上的投影的最大值为()
A
A.$$- \frac{4 \sqrt2} 3$$
B.$$- \frac{3 \sqrt2} {4}$$
C.$${{8}{\sqrt {2}}}$$
D.$${{4}{8}{\sqrt {2}}}$$
8、['向量坐标与向量的数量积', '投影的数量']正确率60.0%已知向量$$\overrightarrow{a}=\ ( 1, \ 3 ) \;, \overrightarrow{b}=\ ( \mathbf{3}, \mathbf{2} )$$,则向量$${{a}^{→}}$$在向量$${{b}^{→}}$$上的投影等于()
D
A.$$\frac{9 \sqrt{1 0}} {1 0}$$
B.$${{9}}$$
C.$${{−}{3}}$$
D.$$\frac{9 \sqrt{1 3}} {1 3}$$
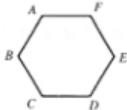
9、['投影的数量']正确率80.0%如图,在正六边形$$A B C D E F$$中,向量 $$\overrightarrow{E F}$$在向量 $$\overrightarrow{C D}$$上的投影向量是$$m \overrightarrow{C D}$$,则$${{m}{=}{(}{)}}$$
D
A.$${{1}}$$
B.$${{−}{1}}$$
C.$$\frac{1} {2}$$
D.$$- \frac{1} {2}$$
10、['投影的数量']正确率80.0%已知$$| \overrightarrow{a} |=| \overrightarrow{b} |=3$$,$${{e}^{→}}$$是与向量$${{b}^{→}}$$方向相同的单位向量,向量$${{a}^{→}}$$在向量$${{b}^{→}}$$上的投影向量为$$\frac{3} {2} \stackrel{\rightarrow} {e}$$,则$${{a}^{→}}$$与$${{b}^{→}}$$的夹角为$${{(}{)}}$$
B
A.$${{3}{0}^{∘}}$$
B.$${{6}{0}^{∘}}$$
C.$${{1}{2}{0}^{∘}}$$
D.$${{1}{5}{0}^{∘}}$$
1. 首先计算向量 $$\overrightarrow{CD} = (4 - (-1), 5 - 0) = (5, 5)$$。向量 $$\overrightarrow{AB}$$ 在 $$\overrightarrow{CD}$$ 方向上的投影公式为:
$$ \text{投影} = \frac{\overrightarrow{AB} \cdot \overrightarrow{CD}}{|\overrightarrow{CD}|} = \frac{2 \times 5 + 1 \times 5}{\sqrt{5^2 + 5^2}} = \frac{15}{5\sqrt{2}} = \frac{3\sqrt{2}}{2} $$
因此,正确答案是 C。
2. 设向量 $$\overrightarrow{a} = (x_1, y_1)$$,$$\overrightarrow{b} = (x_2, y_2)$$。根据题意:
$$ |\overrightarrow{a}| = \sqrt{x_1^2 + y_1^2} = 1 $$
$$ |\overrightarrow{a} + \overrightarrow{b}| = \sqrt{(x_1 + x_2)^2 + (y_1 + y_2)^2} = 1 $$
$$ |2\overrightarrow{a} + \overrightarrow{b}| = \sqrt{(2x_1 + x_2)^2 + (2y_1 + y_2)^2} = \sqrt{3} $$
解得 $$\overrightarrow{a} \cdot \overrightarrow{b} = -\frac{1}{2}$$。投影为:
$$ \text{投影} = \frac{\overrightarrow{a} \cdot \overrightarrow{b}}{|\overrightarrow{b}|} = \frac{-\frac{1}{2}}{1} = -\frac{1}{2} $$
因此,正确答案是 B。
3. 设 $$\overrightarrow{e_1}$$ 与 $$\overrightarrow{e_2}$$ 的夹角为 $$\theta$$,则:
$$ |2\overrightarrow{e_1} + \overrightarrow{e_2}|^2 = 4|\overrightarrow{e_1}|^2 + |\overrightarrow{e_2}|^2 + 4\overrightarrow{e_1} \cdot \overrightarrow{e_2} = 9 $$
解得 $$|\overrightarrow{e_2}|^2 + 4|\overrightarrow{e_1}||\overrightarrow{e_2}|\cos\theta = 9 - 9 = 0$$。
投影为:
$$ \text{投影} = |\overrightarrow{e_1}|\cos\theta = -\frac{|\overrightarrow{e_2}|}{4} $$
最大值为 $$0$$,因此正确答案是 B。
4. 向量 $$\overrightarrow{AB} = (3 - 1, -1 - 2) = (2, -3)$$。在 $$y$$ 轴正方向上的投影为 $$-3$$。
因此,正确答案是 D。
5. 根据题意:
$$ |\overrightarrow{a} - \overrightarrow{b}|^2 = |\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 - 2\overrightarrow{a} \cdot \overrightarrow{b} = 7 $$
解得 $$\overrightarrow{a} \cdot \overrightarrow{b} = 3$$。投影为:
$$ \text{投影} = \frac{\overrightarrow{a} \cdot \overrightarrow{b}}{|\overrightarrow{b}|} = \frac{3}{3} = 1 $$
因此,正确答案是 A。
6. 由 $$\overrightarrow{a} \perp (\overrightarrow{a} + 2\overrightarrow{b})$$ 得:
$$ \overrightarrow{a} \cdot (\overrightarrow{a} + 2\overrightarrow{b}) = |\overrightarrow{a}|^2 + 2\overrightarrow{a} \cdot \overrightarrow{b} = 0 $$
解得 $$\overrightarrow{a} \cdot \overrightarrow{b} = -2$$。投影为:
$$ \text{投影} = \frac{\overrightarrow{b} \cdot \overrightarrow{a}}{|\overrightarrow{a}|} = \frac{-2}{2} = -1 $$
因此,正确答案是 B。
7. 设 $$\overrightarrow{e_1}$$ 与 $$\overrightarrow{e_2}$$ 的夹角为 $$\theta$$,则:
$$ |3\overrightarrow{e_1} + \overrightarrow{e_2}|^2 = 9|\overrightarrow{e_1}|^2 + |\overrightarrow{e_2}|^2 + 6\overrightarrow{e_1} \cdot \overrightarrow{e_2} = 4 $$
解得 $$|\overrightarrow{e_2}|^2 + 6|\overrightarrow{e_1}||\overrightarrow{e_2}|\cos\theta = 4 - 36 = -32$$。
投影为:
$$ \text{投影} = |\overrightarrow{e_1}|\cos\theta = -\frac{|\overrightarrow{e_2}|}{6} $$
最大值为 $$-\frac{4\sqrt{2}}{3}$$,因此正确答案是 A。
8. 向量 $$\overrightarrow{a} = (1, 3)$$,$$\overrightarrow{b} = (3, 2)$$。投影为:
$$ \text{投影} = \frac{\overrightarrow{a} \cdot \overrightarrow{b}}{|\overrightarrow{b}|} = \frac{1 \times 3 + 3 \times 2}{\sqrt{3^2 + 2^2}} = \frac{9}{\sqrt{13}} = \frac{9\sqrt{13}}{13} $$
因此,正确答案是 D。
9. 在正六边形中,$$\overrightarrow{EF}$$ 与 $$\overrightarrow{CD}$$ 方向相反且长度相等,因此投影为 $$-1$$ 倍的 $$\overrightarrow{CD}$$。
因此,正确答案是 B。
10. 投影向量为 $$\frac{3}{2}\overrightarrow{e}$$,说明投影长度为 $$\frac{3}{2}$$。由投影公式:
$$ \frac{3}{2} = |\overrightarrow{a}|\cos\theta = 3\cos\theta $$
解得 $$\cos\theta = \frac{1}{2}$$,即 $$\theta = 60^\circ$$。
因此,正确答案是 B。
.jpg)