1、['数量积的运算律', '向量的数量积的定义', '向量的夹角']正确率60.0%在梯形$${{A}{B}{C}{D}}$$中$$. \; A B / \! / C D, \; \; A D=C D={\frac{1} {2}} A B=2.$$$$\overrightarrow{B D} \cdot\overrightarrow{A C}=-6,$$则$${{∠}{B}{A}{D}}$$的余弦值为()
D
A.$$- \frac{1} {2}$$
B.$$- \frac{1} {3}$$
C.$$\frac{1} {3}$$
D.$$\frac{1} {2}$$
2、['数量积的运算律', '向量的数量积的定义']正确率60.0%已知$$| \boldsymbol{a} |=1, ~ | \boldsymbol{b} |=2,$$向量$${{a}{,}{b}}$$的夹角为$$\frac{\pi} {3},$$则$$a \cdot( a+b )=$$()
C
A.$$\sqrt3-1$$
B.$${{1}}$$
C.$${{2}}$$
D.$$\sqrt3+1$$
3、['向量的模', '向量的数量积的定义', '向量的夹角']正确率60.0%已知向量$${{a}^{→}{,}{{b}^{→}}}$$满足$$\vert\overrightarrow{a} \vert=1, \; \; \vert\overrightarrow{a}+\overrightarrow{b} \vert=\sqrt{7}, \; \; \overrightarrow{a} \cdot( \overrightarrow{b}-\overrightarrow{a} )=-4$$,则$${{a}^{→}}$$与$${{b}^{→}}$$夹角是()
A
A.$$\frac{5 \pi} {6}$$
B.$$\frac{2 \pi} {3}$$
C.$$\frac{\pi} {3}$$
D.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
4、['数量积的运算律', '向量的数量积的定义', '投影的数量']正确率60.0%已知$$A ( 1, 2 ), \, \, \, B ( 2, 4 ), \, \, \, C (-2, 1 ), \, \, \, D (-3, 2 )$$,则向量$$\overrightarrow{C D}$$在向量$$\overrightarrow{A B}$$上的投影为()
A
A.$$\frac{\sqrt{5}} {5}$$
B.$$\frac{2 \sqrt{5}} {5}$$
C.$$\frac{\sqrt2} {2}$$
D.$$\frac{2 \sqrt{2}} {3}$$
5、['数量积的性质', '判断三角形的形状', '向量的数量积的定义', '等比中项']正确率40.0%$${{△}{A}{B}{C}}$$的三个内角$$A. ~ B. ~ C$$成等差数列,$$( \overrightarrow{A B}+\overrightarrow{A C} ) \cdot\overrightarrow{B C}=0$$,则$${{△}{A}{B}{C}}$$一定是()
B
A.直角三角形
B.等边三角形
C.锐角三角形
D.钝角三角形
6、['数量积的运算律', '向量的数量积的定义']正确率60.0%设$${{a}{⃗}{,}{{b}^{⃗}}}$$是平面内的两个单位向量,且夹角为$${{6}{0}^{∘}}$$,则$$| 2 \vec{a}-3 \vec{b} |$$等于()
A
A.$${\sqrt {7}}$$
B.$${\sqrt {{1}{9}}}$$
C.$${{1}}$$
D.$${{5}}$$
7、['数量积的运算律', '向量的数量积的定义', '不等式的性质']正确率40.0%已知向量$$\to, ~ \to, ~ \to$$满足$$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}=\overrightarrow{0},$$且$$\overrightarrow{a}^{2} > \overrightarrow{b}^{2} > \overrightarrow{c}^{2},$$则$$\overrightarrow{a} \cdot\overrightarrow{b}, \overrightarrow{b} \cdot\overrightarrow{c}, \overrightarrow{c} \cdot\overrightarrow{a}$$中最小的值是()
A
A.$${{a}^{→}{⋅}{{b}^{→}}}$$
B.$${{b}^{→}{⋅}{{c}^{→}}}$$
C.$${{c}^{→}{⋅}{{a}^{→}}}$$
D.不能确定的
8、['向量的模', '数量积的性质', '数量积的运算律', '向量的数量积的定义']正确率60.0%已知平面向量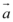 与
与 的夹角为
的夹角为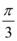 ,且
,且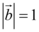 ,
,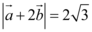 ,则
,则 $${{(}{)}}$$
$${{(}{)}}$$
C
A.$${{1}}$$
B.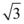
C.$${{2}}$$
D.$${{3}}$$
9、['数量积的运算律', '向量的数量积的定义', '向量的夹角']正确率40.0%已知$$O, ~ A, ~ B, ~ C$$是不共线的四点,若存在一组正实数$$\lambda_{1}, ~ \lambda_{2}, ~ \lambda_{3},$$使$$\lambda_{1} \overrightarrow{O A}+\lambda_{2} \overrightarrow{O B}+\lambda_{3} \overrightarrow{O C}=\overrightarrow{0},$$则三个角$$\angle A O B, \, \, \angle B O C, \, \, \angle C O A$$()
D
A.都是锐角
B.至多有两个钝角
C.恰有两个钝角
D.至少有两个钝角
10、['数量积的性质', '数量积的运算律', '向量的数量积的定义']正确率60.0%已知$$| \overrightarrow{a} |=3, \, \, | \overrightarrow{b} |=5, \, \, | \overrightarrow{a}+\overrightarrow{b} |=7$$,则$${{a}^{→}}$$在$${{b}^{→}}$$方向上的投影为()
C
A.$$- \frac{1} {2}$$
B.$${{1}}$$
C.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
D.$${{2}}$$
1. 题目解析:
在梯形$$ABCD$$中,$$AB \parallel CD$$,$$AD = CD = \frac{1}{2} AB = 2$$。设$$AB = 4$$,$$CD = 2$$。将坐标系原点设在点$$A$$,$$AB$$沿$$x$$轴正方向。设$$A(0,0)$$,$$B(4,0)$$,$$D(x,y)$$,则$$C(x+2,y)$$(因为$$CD = 2$$且$$AB \parallel CD$$)。根据$$AD = 2$$,有$$x^2 + y^2 = 4$$。向量$$\overrightarrow{BD} = (x-4, y)$$,$$\overrightarrow{AC} = (x+2, y)$$。点积$$\overrightarrow{BD} \cdot \overrightarrow{AC} = (x-4)(x+2) + y^2 = x^2 - 2x - 8 + y^2 = -6$$。代入$$x^2 + y^2 = 4$$,得$$4 - 2x - 8 = -6$$,解得$$x = 1$$,$$y = \sqrt{3}$$(取正值)。因此,$$\cos \angle BAD = \frac{\overrightarrow{AB} \cdot \overrightarrow{AD}}{|\overrightarrow{AB}| \cdot |\overrightarrow{AD}|} = \frac{4 \times 1 + 0 \times \sqrt{3}}{4 \times 2} = \frac{1}{2}$$。答案为D。
2. 题目解析:
已知$$|\boldsymbol{a}| = 1$$,$$|\boldsymbol{b}| = 2$$,夹角为$$\frac{\pi}{3}$$。计算$$a \cdot (a + b) = a \cdot a + a \cdot b = |a|^2 + |a||b|\cos \frac{\pi}{3} = 1 + 1 \times 2 \times \frac{1}{2} = 2$$。答案为C。
3. 题目解析:
已知$$|\overrightarrow{a}| = 1$$,$$|\overrightarrow{a} + \overrightarrow{b}| = \sqrt{7}$$,$$\overrightarrow{a} \cdot (\overrightarrow{b} - \overrightarrow{a}) = -4$$。展开点积得$$\overrightarrow{a} \cdot \overrightarrow{b} - |\overrightarrow{a}|^2 = -4$$,即$$\overrightarrow{a} \cdot \overrightarrow{b} = -3$$。设夹角为$$\theta$$,则$$\cos \theta = \frac{\overrightarrow{a} \cdot \overrightarrow{b}}{|\overrightarrow{a}| \cdot |\overrightarrow{b}|} = \frac{-3}{1 \cdot |\overrightarrow{b}|}$$。又$$|\overrightarrow{a} + \overrightarrow{b}|^2 = |\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 + 2 \overrightarrow{a} \cdot \overrightarrow{b} = 7$$,代入得$$1 + |\overrightarrow{b}|^2 - 6 = 7$$,解得$$|\overrightarrow{b}|^2 = 12$$,$$|\overrightarrow{b}| = 2\sqrt{3}$$。因此$$\cos \theta = \frac{-3}{2\sqrt{3}} = -\frac{\sqrt{3}}{2}$$,$$\theta = \frac{5\pi}{6}$$。答案为A。
4. 题目解析:
向量$$\overrightarrow{AB} = (1, 2)$$,$$\overrightarrow{CD} = (-1, 1)$$。投影公式为$$\frac{\overrightarrow{CD} \cdot \overrightarrow{AB}}{|\overrightarrow{AB}|} = \frac{-1 \times 1 + 1 \times 2}{\sqrt{1^2 + 2^2}} = \frac{1}{\sqrt{5}} = \frac{\sqrt{5}}{5}$$。答案为A。
5. 题目解析:
三个内角$$A, B, C$$成等差数列,设$$A = \alpha - d$$,$$B = \alpha$$,$$C = \alpha + d$$,则$$\alpha - d + \alpha + \alpha + d = 180^\circ$$,解得$$B = 60^\circ$$。由$$(\overrightarrow{AB} + \overrightarrow{AC}) \cdot \overrightarrow{BC} = 0$$,利用向量运算得$$(2\overrightarrow{AM}) \cdot \overrightarrow{BC} = 0$$($$M$$为$$BC$$中点),即$$AM \perp BC$$,故$$ABC$$为等腰三角形。结合$$B = 60^\circ$$,$$ABC$$为等边三角形。答案为B。
6. 题目解析:
单位向量$$|\vec{a}| = |\vec{b}| = 1$$,夹角$$60^\circ$$。计算$$|2\vec{a} - 3\vec{b}|^2 = 4|\vec{a}|^2 + 9|\vec{b}|^2 - 12 \vec{a} \cdot \vec{b} = 4 + 9 - 12 \times \frac{1}{2} = 7$$,故$$|2\vec{a} - 3\vec{b}| = \sqrt{7}$$。答案为A。
7. 题目解析:
由$$\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c} = \overrightarrow{0}$$,得$$\overrightarrow{a} \cdot \overrightarrow{b} + \overrightarrow{b} \cdot \overrightarrow{c} + \overrightarrow{c} \cdot \overrightarrow{a} = -\frac{1}{2}(|\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 + |\overrightarrow{c}|^2)$$。由于$$|\overrightarrow{a}|^2 > |\overrightarrow{b}|^2 > |\overrightarrow{c}|^2$$,最小的点积为$$\overrightarrow{b} \cdot \overrightarrow{c}$$。答案为B。
8. 题目解析:
设$$\overrightarrow{a}$$与$$\overrightarrow{b}$$的夹角为$$\theta$$,$$|\overrightarrow{a}| = 1$$,$$|\overrightarrow{b}| = \sqrt{3}$$。由$$|\overrightarrow{a} + \overrightarrow{b}| = 2$$,平方得$$1 + 3 + 2 \times 1 \times \sqrt{3} \cos \theta = 4$$,解得$$\cos \theta = 0$$,$$\theta = \frac{\pi}{2}$$。因此$$\overrightarrow{a} \cdot \overrightarrow{b} = 0$$,$$|\overrightarrow{a} - \overrightarrow{b}|^2 = 1 + 3 - 0 = 4$$,$$|\overrightarrow{a} - \overrightarrow{b}| = 2$$。答案为C。
9. 题目解析:
由$$\lambda_1 \overrightarrow{OA} + \lambda_2 \overrightarrow{OB} + \lambda_3 \overrightarrow{OC} = \overrightarrow{0}$$,可知$$O$$是$$\triangle ABC$$的重心。三个角$$\angle AOB$$、$$\angle BOC$$、$$\angle COA$$中至少有两个钝角。答案为D。
10. 题目解析:
已知$$|\overrightarrow{a}| = 3$$,$$|\overrightarrow{b}| = 5$$,$$|\overrightarrow{a} + \overrightarrow{b}| = 7$$。由$$|\overrightarrow{a} + \overrightarrow{b}|^2 = |\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 + 2 \overrightarrow{a} \cdot \overrightarrow{b}$$,得$$49 = 9 + 25 + 2 \overrightarrow{a} \cdot \overrightarrow{b}$$,解得$$\overrightarrow{a} \cdot \overrightarrow{b} = \frac{15}{2}$$。投影为$$\frac{\overrightarrow{a} \cdot \overrightarrow{b}}{|\overrightarrow{b}|} = \frac{15/2}{5} = \frac{3}{2}$$。答案为C。
题目来源于各渠道收集,若侵权请联系下方邮箱
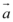 与
与 的夹角为
的夹角为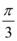 ,且
,且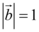 ,
,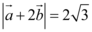 ,则
,则 $${{(}{)}}$$
$${{(}{)}}$$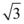
.jpg)