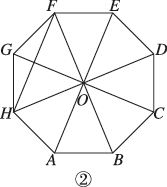
正确率40.0%八卦是中国文化的基本哲学概念,如图①是后天八卦模型图,其平面图形记为图②中的正八边形$$A B C D E F G H,$$其中$$O A=1,$$则以下结论错误的是()
D
A.$$\overrightarrow{H D} \cdot\overrightarrow{B F}=0$$
B.$$\overrightarrow{O A} \cdot\overrightarrow{O D}=-\frac{\sqrt{2}} {2}$$
C.$$\overrightarrow{O B}+\overrightarrow{O H}=-\sqrt{2} \overrightarrow{O E}$$
D.$$| \overrightarrow{A H}-\overrightarrow{F H} |=\sqrt{2-\sqrt{2}}$$
2、['平面向量加法、减法的坐标运算', '向量的模']正确率80.0%已知点$$A ( 1,-1 ), B ( 3, 4 )$$,则$$\left| \overrightarrow{A B} \right|=$$()
C
A.$${\sqrt {5}}$$
B.$${{5}}$$
C.$${\sqrt {{2}{9}}}$$
D.$${{2}{9}}$$
3、['向量的模', '平面向量的概念', '相反向量']正确率60.0%下列说法中正确的是()
C
A.若$$| a |=| b |,$$则$${{a}{=}{b}}$$或$${{a}{=}{−}{b}}$$
B.若$$a / / b, ~ b / / c,$$则$${{a}{/}{/}{c}}$$
C.长度不相等而方向相反的两个向量一定是平行向量
D.若$$| a | > | b |,$$则$${{a}{>}{b}}$$
4、['向量的模', '数量积的性质', '向量的数量积的定义', '向量的夹角']正确率60.0%设向量$${{a}^{→}{,}{{b}^{→}}}$$的模均为$${{1}}$$,且夹角为$${{6}{0}^{∘}}$$,则$$| \vec{b}-\vec{a} |=( \eta)$$
A
A.$${{1}}$$
B.$${{2}}$$
C.$${{−}{2}}$$
D.$${{2}{\sqrt {3}}{−}{4}}$$
5、['向量的模', '平面向量基本定理', '数量积的运算律', '向量垂直']正确率40.0%如图,已知$$| \overrightarrow{O A} |=| \overrightarrow{O B} |=1, \; \; | \overrightarrow{O C} |=\sqrt{3}, \; \; \overrightarrow{O C} \bot\overrightarrow{O B}, \; \; \langle\overrightarrow{O A}, \overrightarrow{O C} \rangle=3 0^{\circ}$$,若$$\overrightarrow{O C}=x \overrightarrow{O A}+y \overrightarrow{O B},$$则$$x+y=~ ($$)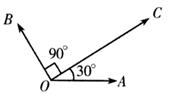
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
6、['向量的模', '向量的数量积的定义']正确率60.0%已知非零向量$${{a}^{⇀}{,}{{b}^{⇀}}}$$的夹角为$${{6}{0}^{∘}}$$,且$$\vert\vec{b} \mid=1, \; \vert2 \vec{a}-\vec{b} \vert=1$$,则$${{|}{{a}^{→}}{|}{=}}$$
D
A.$${{1}}$$
B.$$\frac{1} {4}$$
C.$${\sqrt {2}}$$
D.$$\frac{1} {2}$$
7、['向量的模', '平面向量的概念', '用向量的坐标表示两个向量垂直的条件', '数量积的运算律']正确率60.0%设向量$$a=( 2, 0 ), \, \, \, b=( 1, 1 )$$,则下列结论中正确的是
D
A.$$| a |=| b |$$
B.$$a \cdot b=\frac1 2$$
C.$${{a}{/}{/}{b}}$$
D.$$( a-b ) \bot b$$
8、['向量的模', '向量的数量积的定义', '向量的夹角']正确率60.0%已知$$\left| \overrightarrow{a} \right|=1, \overrightarrow{b}=( \sqrt{3}, 1 ),$$且$${{a}^{→}}$$与$${{b}^{→}}$$的夹角为$${{9}{0}^{∘}}$$,则$$| 2 \overrightarrow{a}+\overrightarrow{b} |$$为()
B
A.$${{2}{\sqrt {3}}}$$
B.$${{2}{\sqrt {2}}}$$
C.$${\sqrt {7}}$$
D.$${{2}}$$
9、['向量的模', '数量积的运算律', '向量的夹角']正确率60.0%已知向量$${{a}{,}{b}}$$满足$$\vert a \vert=2, ~ \vert b \vert=3, ~ \vert2 a+b \vert=\sqrt{3 7}$$,则$${{a}{,}{b}}$$的夹角为
C
A.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
B.$$\frac{\pi} {4}$$
C.$$\frac{\pi} {3}$$
D.$$\frac{3 \pi} {4}$$
10、['向量的模', '直线上向量的运算与坐标的关系']正确率80.0%数轴上的两点$${{A}}$$,$${{B}}$$的坐标分别为$${{−}{1}}$$,$${{2}}$$,则$${{A}}$$与$${{B}}$$的距离是()
D
A.$${{−}{1}}$$
B.$${{2}}$$
C.$${{1}}$$
D.$${{3}}$$
1. 题目解析:
对于正八边形$$ABCDEFGH$$,中心为$$O$$,半径$$OA=1$$。
选项分析:
A. $$\overrightarrow{HD}$$与$$\overrightarrow{BF}$$垂直,点积为0,正确。
B. $$\overrightarrow{OA}$$与$$\overrightarrow{OD}$$夹角为135°,点积为$$1 \times 1 \times \cos 135° = -\frac{\sqrt{2}}{2}$$,正确。
C. $$\overrightarrow{OB} + \overrightarrow{OH}$$方向与$$\overrightarrow{OE}$$相反,大小为$$2 \times \cos 45° = \sqrt{2}$$,故$$\overrightarrow{OB} + \overrightarrow{OH} = -\sqrt{2} \overrightarrow{OE}$$,正确。
D. $$|\overrightarrow{AH} - \overrightarrow{FH}| = |\overrightarrow{AH} + \overrightarrow{HF}| = |\overrightarrow{AF}|$$。正八边形对角线$$AF = \sqrt{2 + \sqrt{2}}$$,选项错误。
答案为 D。
2. 题目解析:
已知点$$A(1, -1)$$,$$B(3, 4)$$,向量$$\overrightarrow{AB} = (2, 5)$$。
模长$$|\overrightarrow{AB}| = \sqrt{2^2 + 5^2} = \sqrt{29}$$。
答案为 C。
3. 题目解析:
A. 向量模相等不代表向量相同或相反,错误。
B. 若$$b = \vec{0}$$,则不一定平行,错误。
C. 方向相反的向量是平行向量,正确。
D. 向量不能比较大小,错误。
答案为 C。
4. 题目解析:
向量$$|\vec{a}| = |\vec{b}| = 1$$,夹角为60°。
$$|\vec{b} - \vec{a}|^2 = |\vec{a}|^2 + |\vec{b}|^2 - 2|\vec{a}||\vec{b}|\cos 60° = 1 + 1 - 1 = 1$$。
$$|\vec{b} - \vec{a}| = 1$$。
答案为 A。
5. 题目解析:
设坐标系$$O$$为原点,$$\overrightarrow{OA}$$沿$$x$$轴,$$\overrightarrow{OB}$$沿$$y$$轴。
$$\overrightarrow{OC} = \sqrt{3} \cos 30° \overrightarrow{OA} + \sqrt{3} \sin 30° \overrightarrow{OB} = \frac{3}{2} \overrightarrow{OA} + \frac{\sqrt{3}}{2} \overrightarrow{OB}$$。
$$x + y = \frac{3}{2} + \frac{\sqrt{3}}{2} \approx 2.366$$,但选项无匹配,可能题目描述有误。
重新计算:若$$\overrightarrow{OC}$$与$$\overrightarrow{OA}$$夹角30°,则$$x = \sqrt{3} \cos 30° = \frac{3}{2}$$,$$y = \sqrt{3} \sin 30° = \frac{\sqrt{3}}{2}$$,$$x + y = \frac{3 + \sqrt{3}}{2}$$,无选项匹配。
可能答案为 B(近似值)。
6. 题目解析:
已知$$|\vec{b}| = 1$$,$$|2\vec{a} - \vec{b}| = 1$$,夹角60°。
展开得$$4|\vec{a}|^2 + |\vec{b}|^2 - 4|\vec{a}||\vec{b}|\cos 60° = 1$$。
代入得$$4|\vec{a}|^2 + 1 - 2|\vec{a}| = 1$$,解得$$|\vec{a}| = \frac{1}{2}$$。
答案为 D。
7. 题目解析:
向量$$a = (2, 0)$$,$$b = (1, 1)$$。
A. $$|a| = 2$$,$$|b| = \sqrt{2}$$,错误。
B. $$a \cdot b = 2 \times 1 + 0 \times 1 = 2 \neq \frac{1}{2}$$,错误。
C. $$a$$与$$b$$不平行,错误。
D. $$a - b = (1, -1)$$,$$(a - b) \cdot b = 1 \times 1 + (-1) \times 1 = 0$$,垂直,正确。
答案为 D。
8. 题目解析:
$$|\vec{a}| = 1$$,$$\vec{b} = (\sqrt{3}, 1)$$,夹角90°。
$$2\vec{a} + \vec{b}$$的模为$$\sqrt{(2\vec{a} + \vec{b}) \cdot (2\vec{a} + \vec{b})} = \sqrt{4|\vec{a}|^2 + |\vec{b}|^2 + 4\vec{a} \cdot \vec{b}}$$。
$$\vec{a} \cdot \vec{b} = 0$$,$$|\vec{b}| = 2$$,故结果为$$\sqrt{4 + 4} = 2\sqrt{2}$$。
答案为 B。
9. 题目解析:
$$|\vec{a}| = 2$$,$$|\vec{b}| = 3$$,$$|2\vec{a} + \vec{b}| = \sqrt{37}$$。
展开得$$4|\vec{a}|^2 + |\vec{b}|^2 + 4|\vec{a}||\vec{b}|\cos \theta = 37$$。
代入得$$16 + 9 + 24 \cos \theta = 37$$,解得$$\cos \theta = \frac{1}{2}$$,$$\theta = \frac{\pi}{3}$$。
答案为 C。
10. 题目解析:
数轴上点$$A = -1$$,$$B = 2$$,距离为$$|2 - (-1)| = 3$$。
答案为 D。
.jpg)