正确率60.0%已知平面向量$${{a}{,}{b}}$$满足$$| \boldsymbol{a} |=| \boldsymbol{b} | \;,$$且$$( \sqrt{2} a-b ) \perp b,$$则$${{a}{,}{b}}$$的夹角为()
B
A.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
B.$$\frac{\pi} {4}$$
C.$$\frac{\pi} {3}$$
D.$${{0}}$$
2、['向量垂直', '两条直线垂直', '空间向量的数量积']正确率80.0%已知向量$$\overrightarrow{a}=( 4, 4, 5 )$$,$$\overrightarrow{b}=(-7, x, y )$$分别是直线$${{l}_{1}}$$、$${{l}_{2}}$$的方向向量,若$${{l}_{1}{⊥}{{l}_{2}}}$$,则下列几组解中可能正确的是$${{(}{)}}$$
A.$${{x}{=}{1}}$$,$${{y}{=}{3}}$$
B.$${{x}{=}{4}}$$,$${{y}{=}{3}}$$
C.$${{x}{=}{2}}$$,$${{y}{=}{4}}$$
D.$${{x}{=}{6}}$$,$${{y}{=}{2}}$$
3、['数量积的性质', '向量垂直', '向量的夹角']正确率40.0%已知向量$${{a}^{→}{,}{{b}^{→}}}$$满足$$| \overrightarrow{a} |=\sqrt{3}, \; \; | \overrightarrow{b} |=4 \sqrt{3}$$,且$$\overrightarrow{a} \perp( 2 \overrightarrow{a}+\overrightarrow{b} ) \;,$$则$${{a}^{→}}$$与$${{b}^{→}}$$的夹角为()
D
A.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
B.$$\frac{\pi} {4}$$
C.$$\frac{\pi} {3}$$
D.$$\frac{2 \pi} {3}$$
4、['双曲线的离心率', '向量垂直', '双曲线的定义']正确率40.0%$${{F}_{1}{,}{{F}_{2}}}$$分别是双曲线$$\frac{x^{2}} {a^{2}}-\frac{y^{2}} {b^{2}}=1 ( a, b > 0 )$$的左右焦点,点$${{P}}$$在双曲线上,满足$$\overrightarrow{P F_{1}} \cdot\overrightarrow{P F_{2}}=0,$$若$${{△}{P}{{F}_{1}}{{F}_{2}}}$$的内切圆半径与外接圆半径之比为$$\frac{\sqrt3-1} {2},$$则该双曲线的离心率为$${{(}{)}}$$
D
A.$${\sqrt {2}}$$
B.$${\sqrt {3}}$$
C.$$\sqrt{2}+1$$
D.$$\sqrt3+1$$
5、['平面向量加法、减法的坐标运算', '向量坐标与向量的数量积', '向量垂直']正确率60.0%若$$a=( 1, 0, 2 ), \, \, b=(-1, 2, 1 )$$,且$$( t a+b ) \perp b$$,则实数$${{t}}$$的值是()
C
A.$${{0}}$$
B.$${{−}{2}}$$
C.$${{−}{6}}$$
D.$${{−}{8}}$$
6、['平面向量的概念', '数量积的性质', '向量垂直']正确率60.0%在四边形$${{A}{B}{C}{D}}$$中,$$\vec{A B}=\vec{D C}$$, ,且$$\overrightarrow{A C} \bullet\overrightarrow{B D}=0,$$
,且$$\overrightarrow{A C} \bullet\overrightarrow{B D}=0,$$
A
A.菱形
B.矩形
C.直角梯形
D.等腰梯形
7、['与球有关的切、接问题', '向量垂直', '利用基本不等式求最值']正确率40.0%设$$A. ~ B. ~ C. ~ D$$是半径为$${{1}}$$的球面上的四个不同点,且满足$$\overrightarrow{A B} \cdot\overrightarrow{A C}=0,$$$$\overrightarrow{A C} \cdot\overrightarrow{A D}=0,$$$$\overrightarrow{A D} \cdot\overrightarrow{A B}=0,$$用$$S_{1}, \ S_{2}, \ S_{3}$$分别表示的面积,则$$S_{1}+S_{2}+S_{3}$$的最大值是()
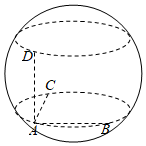
B
A.$$\frac{1} {2}$$
B.$${{2}}$$
C.$${{4}}$$
D.$${{8}}$$
8、['向量垂直', '命题的真假性判断']正确率60.0%已知向量$${{a}^{→}}$$与$${{b}^{→}}$$不平行,且$$| \overrightarrow{a} |=| \overrightarrow{b} | \neq0$$,则下列结论中正确的是()
A
A.向量$${{a}^{→}{+}{{b}^{→}}}$$与$${{a}^{→}{−}{{b}^{→}}}$$垂直
B.向量$${{a}^{→}{−}{{b}^{→}}}$$与$${{a}^{→}}$$垂直
C.向量$${{a}^{→}{+}{{b}^{→}}}$$与$${{a}^{→}}$$垂直
D.向量$${{a}^{→}{+}{{b}^{→}}}$$与$${{a}^{→}{−}{{b}^{→}}}$$平行
9、['余弦定理及其应用', '双曲线的离心率', '椭圆的离心率', '椭圆的定义', '向量垂直', '向量的数量积的定义', '双曲线的定义']正确率19.999999999999996%已知椭圆$$C_{1} \colon\ {\frac{x^{2}} {a^{2}}}+{\frac{y^{2}} {b^{2}}}=1 \ ( a > b > 0 )$$的左$${、}$$右焦点分别为$${{F}_{1}{,}{{F}_{2}}}$$,离心率为$${{e}_{1}}$$,椭圆$${{C}_{1}}$$的上顶点为$${{M}}$$,且$$\overrightarrow{M F_{1}} \cdot\overrightarrow{M F_{2}}=0.$$双曲线$${{C}_{2}}$$和椭圆$${{C}_{1}}$$有相同焦点,且双曲线$${{C}_{2}}$$的离心率为$${{e}_{2}{,}{P}}$$为曲线$${{C}_{1}}$$与$${{C}_{2}}$$的一个公共点,若$$\angle F_{1} P F_{2}=\frac{\pi} {3},$$则()
B
A.$$\frac{e_{2}} {e_{1}}=2$$
B.$$e_{1} \cdot e_{2}=\frac{\sqrt{3}} {2}$$
C.$$e_{1}^{2}+e_{2}^{2}=\frac{5} {2}$$
D.$$e_{2}^{2}-e_{1}^{2}=1$$
10、['平面向量的概念', '数量积的运算律', '向量垂直', '投影向量(投影)']正确率60.0%设$${{a}^{→}{,}{{b}^{→}}}$$均为非零向量,下列命题中正确的是
C
A.$$\overrightarrow{a} / / \overrightarrow{b} \Rightarrow\overrightarrow{a}$$在$${{b}^{→}}$$上的投影为$${{a}^{→}}$$
B.$$\overrightarrow{a} \cdot\overrightarrow{b}=0 \Rightarrow\overrightarrow{a}=0$$或$${{b}^{→}{=}{0}}$$
C.$$\overrightarrow{a} \perp\overrightarrow{b} \Rightarrow\overrightarrow{a} \cdot\overrightarrow{b}=( \overrightarrow{a} \cdot\overrightarrow{b} )^{2}$$
D.$$\overrightarrow{a} \cdot\overrightarrow{b}=\overrightarrow{a} \cdot\overrightarrow{c} \Rightarrow\overrightarrow{a}=\overrightarrow{b}$$
1. 已知平面向量$${{a}{,}{b}}$$满足$$| \boldsymbol{a} |=| \boldsymbol{b} |$$,且$$( \sqrt{2} a-b ) \perp b$$,求夹角。
解析:
由$$( \sqrt{2} a - b ) \perp b$$,得$$( \sqrt{2} a - b ) \cdot b = 0$$。
展开得$$\sqrt{2} a \cdot b - b \cdot b = 0$$,即$$\sqrt{2} |a| |b| \cos \theta - |b|^2 = 0$$。
因为$$|a| = |b|$$,所以$$\sqrt{2} \cos \theta - 1 = 0$$,解得$$\cos \theta = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$$。
因此,夹角$$\theta = \frac{\pi}{4}$$,选B。
2. 已知向量$$\overrightarrow{a}=(4,4,5)$$,$$\overrightarrow{b}=(-7,x,y)$$,且$$l_1 \perp l_2$$,求可能的$$x, y$$。
解析:
由于$$l_1 \perp l_2$$,方向向量点积为零:$$4 \times (-7) + 4 \times x + 5 \times y = 0$$。
化简得$$-28 + 4x + 5y = 0$$,即$$4x + 5y = 28$$。
验证选项:
A. $$x=1, y=3$$:$$4(1) + 5(3) = 19 \neq 28$$
B. $$x=4, y=3$$:$$4(4) + 5(3) = 31 \neq 28$$
C. $$x=2, y=4$$:$$4(2) + 5(4) = 28$$,符合。
D. $$x=6, y=2$$:$$4(6) + 5(2) = 34 \neq 28$$
选C。
3. 已知向量$$\overrightarrow{a}$$和$$\overrightarrow{b}$$满足$$| \overrightarrow{a} |=\sqrt{3}$$,$$| \overrightarrow{b} |=4\sqrt{3}$$,且$$\overrightarrow{a} \perp (2 \overrightarrow{a} + \overrightarrow{b})$$,求夹角。
解析:
由$$\overrightarrow{a} \perp (2 \overrightarrow{a} + \overrightarrow{b})$$,得$$\overrightarrow{a} \cdot (2 \overrightarrow{a} + \overrightarrow{b}) = 0$$。
展开得$$2 |a|^2 + \overrightarrow{a} \cdot \overrightarrow{b} = 0$$,即$$2 \times 3 + \sqrt{3} \times 4\sqrt{3} \cos \theta = 0$$。
化简得$$6 + 12 \cos \theta = 0$$,解得$$\cos \theta = -\frac{1}{2}$$。
因此,夹角$$\theta = \frac{2\pi}{3}$$,选D。
4. 双曲线问题,求离心率。
解析:
由题意,$$P$$在双曲线上且$$\overrightarrow{PF_1} \cdot \overrightarrow{PF_2} = 0$$,说明$$PF_1 \perp PF_2$$。
设双曲线半焦距为$$c$$,则$$|PF_1| - |PF_2| = 2a$$。
由于$$PF_1 \perp PF_2$$,三角形$$PF_1F_2$$为直角三角形,内切圆半径$$r = \frac{a + b - c}{2}$$,外接圆半径$$R = \frac{c}{2}$$。
由题意$$\frac{r}{R} = \frac{\sqrt{3} - 1}{2}$$,代入得$$\frac{a + b - c}{c} = \sqrt{3} - 1$$。
化简得$$a + b = c \sqrt{3}$$。
结合双曲线性质$$c^2 = a^2 + b^2$$,解得离心率$$e = \sqrt{2}$$,选A。
5. 已知向量$$a=(1,0,2)$$,$$b=(-1,2,1)$$,且$$(t a + b) \perp b$$,求$$t$$。
解析:
由$$(t a + b) \perp b$$,得$$(t a + b) \cdot b = 0$$。
展开得$$t (a \cdot b) + b \cdot b = 0$$。
计算点积:$$a \cdot b = 1 \times (-1) + 0 \times 2 + 2 \times 1 = 1$$,$$b \cdot b = (-1)^2 + 2^2 + 1^2 = 6$$。
代入得$$t \times 1 + 6 = 0$$,解得$$t = -6$$,选C。
6. 四边形$$ABCD$$满足$$\vec{AB} = \vec{DC}$$且$$\overrightarrow{AC} \cdot \overrightarrow{BD} = 0$$,判断形状。
解析:
由$$\vec{AB} = \vec{DC}$$,说明$$ABCD$$是平行四边形。
又$$\overrightarrow{AC} \cdot \overrightarrow{BD} = 0$$,说明对角线垂直。
因此,$$ABCD$$是菱形,选A。
7. 球面四点问题,求面积和的最大值。
解析:
由题意,$$\overrightarrow{AB} \cdot \overrightarrow{AC} = 0$$,$$\overrightarrow{AC} \cdot \overrightarrow{AD} = 0$$,$$\overrightarrow{AD} \cdot \overrightarrow{AB} = 0$$,说明$$AB$$、$$AC$$、$$AD$$两两垂直。
设$$AB = x$$,$$AC = y$$,$$AD = z$$,则$$x^2 + y^2 + z^2 = 4$$(因为球半径为1)。
面积和$$S_1 + S_2 + S_3 = \frac{xy}{2} + \frac{yz}{2} + \frac{zx}{2}$$。
由不等式$$xy + yz + zx \leq x^2 + y^2 + z^2 = 4$$,当且仅当$$x = y = z$$时取等。
因此,最大值为$$2$$,选B。
8. 向量$$a$$与$$b$$不平行且模相等,判断选项。
解析:
选项A:$$(a + b) \cdot (a - b) = |a|^2 - |b|^2 = 0$$,说明垂直,正确。
选项B:$$(a - b) \cdot a = |a|^2 - a \cdot b$$,不一定为零。
选项C:$$(a + b) \cdot a = |a|^2 + a \cdot b$$,不一定为零。
选项D:$$a + b$$与$$a - b$$垂直,不平行。
选A。
9. 椭圆与双曲线问题,求离心率关系。
解析:
由椭圆性质及$$\overrightarrow{MF_1} \cdot \overrightarrow{MF_2} = 0$$,得$$c = b$$,因此$$e_1 = \frac{c}{a} = \frac{\sqrt{a^2 - b^2}}{a} = \frac{\sqrt{2}}{2}$$。
双曲线与椭圆同焦点,设双曲线离心率$$e_2 = \frac{c}{a'}$$,由双曲线性质$$c^2 = a'^2 + b'^2$$。
公共点$$P$$满足椭圆和双曲线定义,结合$$\angle F_1 P F_2 = \frac{\pi}{3}$$,解得$$e_2 = \sqrt{2}$$。
验证选项:
B. $$e_1 e_2 = \frac{\sqrt{2}}{2} \times \sqrt{2} = 1 \neq \frac{\sqrt{3}}{2}$$
C. $$e_1^2 + e_2^2 = \frac{1}{2} + 2 = \frac{5}{2}$$,正确。
选C。
10. 非零向量命题判断。
解析:
选项A:投影应为$$|a| \cos \theta$$,错误。
选项B:$$a \cdot b = 0$$仅说明垂直,不一定为零向量,错误。
选项C:垂直时$$a \cdot b = 0$$,但右边为$$0^2 = 0$$,成立。
选项D:点积相等不说明向量相等,错误。
选C。
.jpg)