正确率60.0%在$${{△}{A}{B}{C}}$$中,若$$| \overrightarrow{A B}+\overrightarrow{A C} |=| \overrightarrow{A B}-\overrightarrow{A C} |,$$$$A B=2, \, A C=1, \, E, \, F$$分别为$${{B}{C}}$$边上靠近$${{B}{,}{C}}$$的三等分点,则$$\overrightarrow{A E} \cdot\overrightarrow{A F}=$$()
B
A.$$\frac{8} {9}$$
B.$$\frac{1 0} {9}$$
C.$$\frac{2 5} {9}$$
D.$$\frac{2 6} {9}$$
2、['向量的模', '数量积的性质']正确率60.0%已知向量$${{a}{⃗}{,}{{b}^{⃗}}}$$的夹角为$${{6}{0}^{∘}}$$,且$$\left\vert\vec{a} \right\vert=\left\vert\vec{b} \right\vert=1,$$则$$\left| \vec{a}+\vec{b} \right|$$等于$${{(}{)}}$$
B
A.$${{3}}$$
B.$${\sqrt {3}}$$
C.$${{2}}$$
D.$${{1}}$$
3、['平面向量加法、减法的坐标运算', '数量积的性质', '用向量的坐标表示两个向量垂直的条件']正确率60.0%已知向量$$\overrightarrow{a}=( 1, 2 ), \; \; \overrightarrow{a}-\overrightarrow{b}=( 4, 5 ), \; \; \overrightarrow{c}=( m, 3 ),$$若$$( 2 \overrightarrow{a}+\overrightarrow{b} ) \perp\overrightarrow{c}$$,则$${{m}{=}{(}{)}}$$
A
A.$${{3}}$$
B.$${{4}}$$
C.$${{−}{3}}$$
D.$$\frac{3} {5}$$
4、['数量积的性质', '平面向量的概念', '向量的数量积的定义']正确率60.0%已知$${{a}^{→}{、}{{b}^{→}}}$$是两个单位向量,那么下列命题中的真命题是()
D
A.$${{a}^{→}{=}{{b}^{→}}}$$
B.$$\overrightarrow{a} \cdot\overrightarrow{b}=0$$
C.$$| \overrightarrow{a} \cdot\overrightarrow{b} | < 1$$
D.$$\overrightarrow{a}^{2}=\overrightarrow{b}^{2}$$
5、['向量的模', '数量积的性质', '数量积的运算律', '向量的数量积的定义', '向量的夹角']正确率40.0%已知$$\vert\overrightarrow{a} \vert=\sqrt{2}, \; \vert\overrightarrow{b} \vert=1, \; \overrightarrow{a} \cdot( \overrightarrow{a}-\overrightarrow{b} )=1$$,则向量$${{a}^{→}}$$与向量$${{b}^{→}}$$的夹角为
C
A.$$\frac{2 \pi} {3}$$
B.$$\frac{\pi} {3}$$
C.$$\frac{\pi} {4}$$
D.$$\begin{array} {l l} {\pi} \\ {\frac{\pi} {6}} \\ \end{array}$$
6、['数量积的性质', '数量积的运算律', '向量的数量积的定义']正确率40.0%已知非零向量$${{a}^{→}{,}{{b}^{→}}}$$满足$$| \overrightarrow{a} |=\lambda| \overrightarrow{b} |$$,若$${{a}^{→}{,}{{b}^{→}}}$$夹角的余弦值为$$\frac{1 9} {3 0},$$且$$( \begin{matrix} {\overrightarrow{a}} \\ \end{matrix}-2 \begin{matrix} {\overrightarrow{b}} \\ \end{matrix} ) \perp\begin{matrix} {( 3 \overrightarrow{a}+\overrightarrow{b}} \\ \end{matrix} )$$,则实数$${{λ}}$$的值为()
D
A.$$- \frac{4} {9}$$
B.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
C.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$或$$- \frac{4} {9}$$
D.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
7、['向量的模', '数量积的性质', '向量垂直']正确率60.0%正方形$${{A}{B}{C}{D}}$$边长为$${{2}}$$,点$${{E}}$$为$${{B}{C}}$$边的中点,$${{F}}$$为$${{C}{D}}$$边上一点,若$$\overrightarrow{A F} \cdot\overrightarrow{A E}=\left| \overrightarrow{A E} \right|^{2},$$则$$| \overrightarrow{A F} |=( \textsubscript{)}$$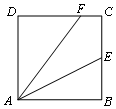
D
A.$${{3}}$$
B.$${{5}}$$
C.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
D.$$\frac{5} {2}$$
8、['向量的模', '数量积的性质', '向量坐标与向量的数量积', '向量的数量积的定义', '向量的夹角']正确率60.0%已知向量$$\stackrel{\rightarrow} {a}=( 1, \sqrt{3} ), \ \stackrel{\rightarrow} {| b |}=3,$$且$$\begin{array} {c c} {\to} \\ {a} \\ \end{array}$$与$$\begin{array} {c c} {\rightarrow} \\ {b} \\ \end{array}$$的夹角为$$\frac{\pi} {3},$$则$$| 2 \stackrel{\rightarrow} {a}+\stackrel{\rightarrow} {b} |=( \textit{} )$$
B
A.$${{5}}$$
B.$${\sqrt {{3}{7}}}$$
C.$${{7}}$$
D.$${{3}{7}}$$
9、['数量积的性质', '数量积的运算律', '向量的数量积的定义']正确率60.0%已知向量$${{a}^{→}}$$与$${{a}^{→}{+}{{b}^{→}}}$$的夹角为$$6 0^{\circ}, ~ | \overrightarrow{a} |=1, ~ | \overrightarrow{b} |=\sqrt{3}$$,则$$\overrightarrow{a} \cdot\overrightarrow{b}=$$()
A
A.$${{0}}$$
B.$$- \frac{\sqrt3} {2}$$
C.$$- \frac{3} {2}$$
D.$${{0}}$$或$$- \frac{3} {2}$$
10、['向量的模', '数量积的性质', '向量的数量积的定义']正确率60.0%已知平面向量$${{a}^{→}}$$与$${{b}^{→}}$$的夹角为$$\frac{2 \pi} {3},$$若$$\overrightarrow{a}=( \; \sqrt{3} \;, \;-1 \; ), \; \; | \overrightarrow{a}-2 \overrightarrow{b} |=2 \sqrt{1 3}.$$则$$\vert\overrightarrow{b} \vert=($$)
A
A.$${{3}}$$
B.$${{4}}$$
C.$${\sqrt {3}}$$
D.$${{2}}$$
1. 在三角形 $$ABC$$ 中,由 $$| \overrightarrow{AB} + \overrightarrow{AC} | = | \overrightarrow{AB} - \overrightarrow{AC} |$$ 可知,$$AB$$ 与 $$AC$$ 互相垂直。因此,$$ABC$$ 是直角三角形,$$A$$ 为直角顶点。
2. 已知 $$|\vec{a}| = |\vec{b}| = 1$$,夹角为 $$60^\circ$$。
3. 已知 $$\vec{a} = (1, 2)$$,$$\vec{a} - \vec{b} = (4, 5)$$,则 $$\vec{b} = \vec{a} - (4, 5) = (-3, -3)$$。
4. 对于单位向量 $$\vec{a}$$ 和 $$\vec{b}$$:
5. 已知 $$|\vec{a}| = \sqrt{2}$$,$$|\vec{b}| = 1$$,$$\vec{a} \cdot (\vec{a} - \vec{b}) = 1$$。
6. 由 $$(\vec{a} - 2\vec{b}) \perp (3\vec{a} + \vec{b})$$,点积为 $$0$$:
7. 设正方形 $$ABCD$$ 的坐标系为 $$A(0,0)$$,$$B(2,0)$$,$$C(2,2)$$,$$D(0,2)$$。
8. 已知 $$\vec{a} = (1, \sqrt{3})$$,$$|\vec{b}| = 3$$,夹角为 $$\frac{\pi}{3}$$。
9. 设 $$\vec{a}$$ 与 $$\vec{a} + \vec{b}$$ 的夹角为 $$60^\circ$$,$$|\vec{a}| = 1$$,$$|\vec{b}| = \sqrt{3}$$。
10. 已知 $$\vec{a} = (\sqrt{3}, -1)$$,$$|\vec{a}| = 2$$,夹角为 $$\frac{2\pi}{3}$$。
.jpg)