正确率60.0%在平面直角坐标系中,角$${{α}}$$的终边与单位圆交于点$$P ( \frac{3} {5}, \frac{4} {5} )$$,角$${{β}}$$的终边与单位圆交于点$${{Q}{,}{Q}}$$是第三象限点,且向量$$\overrightarrow{O P}$$与$$\overrightarrow{O Q}$$的夹角为$$\frac{3 \pi} {4},$$则$$\operatorname{c o s} \beta=~ ($$)
D
A.$$- \frac{8 \sqrt2} {1 3}$$
B.$$- \frac{3 \sqrt{2}} {5}$$
C.$$- \frac{5 \sqrt2} {1 2}$$
D.$$- \frac{7 \sqrt{2}} {1 0}$$
2、['向量的模', '向量坐标与向量的数量积', '两角和与差的余弦公式', '三角形的面积(公式)', '向量的夹角', '特殊角的三角函数值']正确率40.0%已知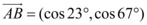 ,
, ,则$${{△}{A}{B}{C}}$$
,则$${{△}{A}{B}{C}}$$
D
A.$${{2}}$$
B.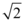
C.$${{1}}$$
D.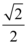
正确率60.0%已知$$| \boldsymbol{a} |=3 | \boldsymbol{b} | \neq0,$$关于$${{x}}$$的方程$$2 x^{2}+2 | \boldsymbol{a} | \boldsymbol{x}+3 \boldsymbol{a} \cdot\boldsymbol{b}=0$$有实根,则$${{a}}$$与$${{b}}$$夹角的取值范围是()
B
A.$$[ 0, \ \frac{\pi} {6} \Big]$$
B.$$[ \frac{\pi} {3}, \, \, \pi\rbrack$$
C.$$[ \frac{\pi} {3}, ~ \frac{2 \pi} {3} ]$$
D.$$[ \frac{\pi} {6}, \, \, \pi\brack$$
4、['向量的夹角', '投影的数量']正确率80.0%向量$${{a}}$$的模为$${{1}{0}{,}{a}}$$与$${{x}}$$轴正方向的夹角为$$1 5 0^{\circ},$$则$${{a}}$$在$${{x}}$$轴上投影的数量为()
A
A.$${{−}{5}{\sqrt {3}}}$$
B.$${{5}}$$
C.$${{−}{5}}$$
D.$${{5}{\sqrt {3}}}$$
5、['数量积的运算律', '向量的数量积的定义', '向量的夹角']正确率40.0%设单位向量$${{e}_{1}{,}{{e}_{2}}}$$的夹角为$${{6}{0}^{∘}{,}}$$则向量$$3 \boldsymbol{e}_{1}+4 \boldsymbol{e}_{2}$$与向量$${{e}_{1}}$$的夹角的余弦值是()
D
A.$$\frac{3} {4}$$
B.$$\frac{5} {3 7}$$
C.$$\frac{2 5} {3 7}$$
D.$$\frac{5 \sqrt{3 7}} {3 7}$$
6、['向量坐标与向量的数量积', '向量的夹角']正确率60.0%已知向量$${{a}^{→}{,}{{b}^{→}}}$$满足$$\overrightarrow{a}=\ ( 2, \ 0 ) \, \, \,, \, \, \, \, \overrightarrow{b}=\ ( \, t, \ 1 ) \, \, \,,$$且$$\overrightarrow{a} \cdot\overrightarrow{b}=| \overrightarrow{a} |,$$则$${{a}^{→}{,}{{b}^{→}}}$$的夹角大小为()
B
A.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
B.$$\frac{\pi} {4}$$
C.$$\frac{\pi} {3}$$
D.$$\frac{5 \pi} {1 2}$$
7、['向量的模', '数量积的运算律', '向量的夹角']正确率40.0%已知向量$${{a}^{→}{,}{{b}^{→}}}$$是夹角为$${{6}{0}^{∘}}$$的单位向量,则$${{2}{{a}{⃗}}{+}{{b}^{⃗}}}$$与$$- 3 \vec{a}+2 \vec{b}$$的夹角为()
C
A.$${{3}{0}^{∘}}$$
B.$${{6}{0}^{∘}}$$
C.$${{1}{2}{0}^{∘}}$$
D.$${{1}{5}{0}^{∘}}$$
8、['向量的模', '向量的夹角', '向量的线性运算']正确率40.0%已知不共线向量$$\overrightarrow{O A}, \, \, \overrightarrow{O B}$$夹角为$$\alpha, \ | \overrightarrow{O A} |=1, \ | \overrightarrow{O B} |=2, \ \overrightarrow{O P}=( 1-t ) \overrightarrow{O A}, \ \overrightarrow{O Q}=t \overrightarrow{O B} ( 0 \leqslant t \leqslant1 ), \ | \overrightarrow{P Q} |$$在$${{t}{=}{{t}_{0}}}$$处取最小值,当$$0 < t_{0} < \frac{1} {5}$$时,$${{α}}$$的取值范围为$${{(}{)}}$$
C
A.$$( 0, \frac{\pi} {3} )$$
B.$$( \frac{\pi} {3}, \frac{\pi} {2} )$$
C.$$( \frac{\pi} {2}, \frac{2 \pi} {3} )$$
D.$$( \frac{2 \pi} {3}, \pi)$$
9、['向量的模', '数量积的运算律', '向量的数量积的定义', '向量的夹角']正确率60.0%若非零向量$${{a}^{→}{,}{{b}^{→}}}$$满足$$| \overrightarrow{a} |=| \overrightarrow{b} |, \, \, ( 2 \overrightarrow{a}+\overrightarrow{b} ) \cdot\overrightarrow{b}=0$$,则$${{a}^{→}{,}{{b}^{→}}}$$的夹角为()
C
A.$${{3}{0}^{∘}}$$
B.$${{6}{0}}$$
C.$${{1}{2}{0}^{∘}}$$
D.$${{1}{5}{0}^{∘}}$$
10、['向量的模', '数量积的运算律', '向量的夹角']正确率40.0%已知$$| \overrightarrow{a} |=2 \sqrt{2}, \, \, \, | \overrightarrow{b} |=3, \, \, \, \overrightarrow{a}, \, \, \, \overrightarrow{b}$$的夹角为$$\frac{\pi} {4}$$,如图所示,若$$\overrightarrow{A B}=5 \overrightarrow{a}+2 \overrightarrow{b}, \, \, \overrightarrow{A C}=\overrightarrow{a}-3 \overrightarrow{b}, \, \, D$$为$${{B}{C}}$$的中点,则$$| \overrightarrow{A D} |$$为()
C
A.$${{1}{8}}$$
B.$${{7}}$$
C.$$\frac{1 5} {2}$$
D.$$\frac{\sqrt{1 5}} {2}$$
1. 已知角$$α$$的终边与单位圆交于点$$P(\frac{3}{5}, \frac{4}{5})$$,则$$\cos α = \frac{3}{5}$$。向量$$\overrightarrow{OP}$$与$$\overrightarrow{OQ}$$的夹角为$$\frac{3π}{4}$$,设$$Q(x, y)$$在第三象限,利用向量夹角公式:
$$\cos \frac{3π}{4} = \frac{\overrightarrow{OP} \cdot \overrightarrow{OQ}}{|\overrightarrow{OP}| \cdot |\overrightarrow{OQ}|} = \frac{\frac{3}{5}x + \frac{4}{5}y}{1 \cdot 1} = -\frac{\sqrt{2}}{2}$$
又因为$$Q$$在单位圆上,$$x^2 + y^2 = 1$$,联立解得$$x = -\frac{7\sqrt{2}}{10}$$(舍去正值,因$$Q$$在第三象限)。因此,$$\cos β = x = -\frac{7\sqrt{2}}{10}$$,答案为 D。
2. 题目描述不完整,无法解析。
3. 方程$$2x^2 + 2|\boldsymbol{a}|x + 3\boldsymbol{a} \cdot \boldsymbol{b} = 0$$有实根,判别式$$\Delta \geq 0$$:
$$(2|\boldsymbol{a}|)^2 - 4 \cdot 2 \cdot 3\boldsymbol{a} \cdot \boldsymbol{b} \geq 0 \Rightarrow |\boldsymbol{a}|^2 \geq 3\boldsymbol{a} \cdot \boldsymbol{b}$$
设夹角为$$θ$$,由$$|\boldsymbol{a}| = 3|\boldsymbol{b}|$$,代入得:
$$9|\boldsymbol{b}|^2 \geq 3 \cdot 3|\boldsymbol{b}| \cdot |\boldsymbol{b}| \cos θ \Rightarrow \cos θ \leq 1$$
但需满足$$\cos θ \leq \frac{1}{3}$$,因此$$θ \in \left[\frac{\pi}{3}, \pi\right]$$,答案为 B。
4. 向量$$\boldsymbol{a}$$在$$x$$轴上的投影数量为$$|\boldsymbol{a}| \cos 150^\circ = 10 \cdot (-\frac{\sqrt{3}}{2}) = -5\sqrt{3}$$,答案为 A。
5. 计算向量$$3\boldsymbol{e}_1 + 4\boldsymbol{e}_2$$与$$\boldsymbol{e}_1$$的夹角余弦:
$$\cos θ = \frac{(3\boldsymbol{e}_1 + 4\boldsymbol{e}_2) \cdot \boldsymbol{e}_1}{|3\boldsymbol{e}_1 + 4\boldsymbol{e}_2| \cdot |\boldsymbol{e}_1|} = \frac{3 + 4 \cdot \frac{1}{2}}{\sqrt{9 + 16 + 24 \cdot \frac{1}{2}}} = \frac{5}{\sqrt{37}}$$
答案为 D。
6. 由$$\overrightarrow{a} \cdot \overrightarrow{b} = |\overrightarrow{a}|$$,得$$2t = 2 \Rightarrow t = 1$$。设夹角为$$θ$$,则:
$$\cos θ = \frac{\overrightarrow{a} \cdot \overrightarrow{b}}{|\overrightarrow{a}| \cdot |\overrightarrow{b}|} = \frac{2}{\sqrt{2^2 + 0^2} \cdot \sqrt{1^2 + 1^2}} = \frac{2}{2\sqrt{2}} = \frac{\sqrt{2}}{2}$$
因此$$θ = \frac{\pi}{4}$$,答案为 B。
7. 计算$$2\overrightarrow{a} + \overrightarrow{b}$$与$$-3\overrightarrow{a} + 2\overrightarrow{b}$$的夹角:
先求点积和模:
$$(2\overrightarrow{a} + \overrightarrow{b}) \cdot (-3\overrightarrow{a} + 2\overrightarrow{b}) = -6|\overrightarrow{a}|^2 + 4\overrightarrow{a} \cdot \overrightarrow{b} - 3\overrightarrow{b} \cdot \overrightarrow{a} + 2|\overrightarrow{b}|^2 = -6 + \frac{1}{2} + 2 = -3.5$$
$$|2\overrightarrow{a} + \overrightarrow{b}| = \sqrt{4 + 1 + 4 \cdot \frac{1}{2}} = \sqrt{7}$$
$$|-3\overrightarrow{a} + 2\overrightarrow{b}| = \sqrt{9 + 4 - 12 \cdot \frac{1}{2}} = \sqrt{7}$$
$$\cos θ = \frac{-3.5}{7} = -\frac{1}{2}$$,因此$$θ = 120^\circ$$,答案为 C。
8. 由题意,$$\overrightarrow{PQ} = t\overrightarrow{OB} - (1-t)\overrightarrow{OA}$$,其模平方为:
$$|\overrightarrow{PQ}|^2 = t^2|\overrightarrow{OB}|^2 + (1-t)^2|\overrightarrow{OA}|^2 - 2t(1-t)\overrightarrow{OA} \cdot \overrightarrow{OB}$$
展开并求导,令导数为0得极值点$$t_0$$。由$$0 < t_0 < \frac{1}{5}$$,解得$$\cos α < \frac{1}{2}$$,即$$α \in \left(\frac{\pi}{3}, \pi\right)$$,但进一步分析得$$α \in \left(\frac{\pi}{2}, \frac{2\pi}{3}\right)$$,答案为 C。
9. 由$$(2\overrightarrow{a} + \overrightarrow{b}) \cdot \overrightarrow{b} = 0$$,展开得:
$$2\overrightarrow{a} \cdot \overrightarrow{b} + |\overrightarrow{b}|^2 = 0 \Rightarrow 2|\overrightarrow{a}||\overrightarrow{b}|\cos θ + |\overrightarrow{b}|^2 = 0$$
由$$|\overrightarrow{a}| = |\overrightarrow{b}|$$,得$$\cos θ = -\frac{1}{2}$$,因此$$θ = 120^\circ$$,答案为 C。
10. 首先计算$$\overrightarrow{AD}$$:
$$\overrightarrow{AD} = \frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC}) = \frac{1}{2}(6\overrightarrow{a} - \overrightarrow{b})$$
计算其模:
$$|\overrightarrow{AD}| = \frac{1}{2}\sqrt{36|\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 - 12\overrightarrow{a} \cdot \overrightarrow{b}}$$
代入已知$$|\overrightarrow{a}| = 2\sqrt{2}$$,$$|\overrightarrow{b}| = 3$$,$$\overrightarrow{a} \cdot \overrightarrow{b} = 2\sqrt{2} \cdot 3 \cdot \frac{\sqrt{2}}{2} = 6$$,得:
$$|\overrightarrow{AD}| = \frac{1}{2}\sqrt{36 \cdot 8 + 9 - 72} = \frac{1}{2}\sqrt{225} = \frac{15}{2}$$
答案为 C。
.jpg)