.jpg)
正确率80.0%为了得到函数$$y=\operatorname{s i n} \， 3 x+\operatorname{c o s} \， 3 x+1$$的图象，可以将函数$$y=\sqrt{2} \operatorname{s i n} \， 3 x$$的图象$${{(}{)}}$$
A.向右平移$$\frac{\pi} {1 2}$$个单位，向下平移$${{1}}$$个单位
B.向左平移$$\frac{\pi} {1 2}$$个单位，向下平移$${{1}}$$个单位
C.向右平移$$\frac{\pi} {1 2}$$个单位，向上平移$${{1}}$$个单位
D.向左平移$$\frac{\pi} {1 2}$$个单位，向上平移$${{1}}$$个单位
2、['函数y=A sin(wx+φ)（A≠0，w不等于0）的图象及性质'， '正弦曲线的对称轴'， '三角函数的图象变换']正确率60.0%已知点$$A ( 0， 2 \sqrt{3} )， \， \， \， B ( \frac{\pi} {6}， 0 )$$是函数，$$f ( x )=4 \operatorname{s i n} ( \omega x+\varphi) ( 0 < \omega< 6， \frac{\pi} {2} < \varphi< \pi)$$的图象上的两个点，若将函数$${{f}{(}{x}{)}}$$的图象向右平移$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$个单位长度，得到函数$${{g}{(}{x}{)}}$$的图象，则函数$${{g}{(}{x}{)}}$$的图象的一条对称轴的方程为
A
A.$$x=\frac{\pi} {1 2}$$
B.$$x=\frac{\pi} {6}$$
C.$$x=\frac{\pi} {3}$$
D.$$x=\frac{5 \pi} {1 2}$$
3、['函数y=A sin(wx+φ)（A≠0，w不等于0）的图象及性质'， '由图象（表）求三角函数的解析式'， '三角函数的图象变换']正确率40.0%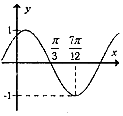
函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=A \sin\left( \begin{matrix} {\omega x+\varphi} \\ \end{matrix} \right) \ \left( \begin{matrix} {A > 0， \left| \varphi\right| < \frac{\pi} {2}} \\ \end{matrix} \right)$$
D
A.向左平移$$\frac{\pi} {3}$$个单位
B.向右平移$$\frac{\pi} {3}$$个单位
C.向左平移$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$个单位
D.向右平移$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$个单位
4、['函数y=A sin(wx+φ)（A≠0，w不等于0）的图象及性质'， '正弦（型）函数的单调性'， '正弦（型）函数的周期性']正确率40.0%已知函数$$y=2 \operatorname{s i n} ( \omega x+\varphi) ( \omega> 0， | \varphi| < \frac{\pi} {2} )$$的部分图象如图所示，则函数$${{f}{(}{x}{)}}$$的一个单调递增区间是
B
A.$$[-\frac{\pi} {1 2}，-\frac{7 \pi} {1 2} ]$$
B.$$[-\frac{\pi} {1 2}， \frac{5 \pi} {1 2} ]$$
C.$$[-\frac{7 \pi} {1 2}， \frac{5 \pi} {1 2} ]$$
D.$$[-\frac{7 \pi} {1 2}，-\frac{\pi} {1 2} ]$$
5、['函数y=A sin(wx+φ)（A≠0，w不等于0）的图象及性质'， '辅助角公式']正确率40.0%函数$$f ( x )=\operatorname{s i n} ( 2 x+\theta)-\sqrt{3} \operatorname{c o s} ( 2 x+\theta)$$$$( 0 < \theta< \pi)$$，对于任意$${{x}{∈}{R}}$$，都有$$f ( x ) \leq f ( \frac{\pi} {6} )$$，若$$x_{1}， x_{2} \in\left( \frac{\pi} {6}， \frac{2 \pi} {3} \right)$$，且$$f ( x_{1} )=-f ( x_{2} )$$，则$$f ( x_{1}+x_{2} )=$$（）
C
A.$$\frac{\sqrt3} {2}$$
B.$$- \frac{\sqrt3} {2}$$
C.$${{−}{1}}$$
D.$${{1}}$$
6、['函数y=A sin(wx+φ)（A≠0，w不等于0）的图象及性质'， '正弦（型）函数的定义域和值域'， '三角函数的图象变换']正确率60.0%已知函数$$f \ ( \ x ) \ =2 \operatorname{s i n} \omega x \ ( \ 0 < \omega< 3 )$$的图象关于直线$$x=\frac{\pi} {4}$$对称，将$${{f}{（}{x}{）}}$$的图象向右平移$$\frac{\pi} {3}$$个单位，再向上平移$${{1}}$$个单位可以得到函数$${{g}{（}{x}}$$的图象，则$${{g}{（}{x}{）}}$$在区间$$[-\frac{\pi} {3}， \ \frac{\pi} {2} ]$$上的值域是（）
A
A.$$[-1， ~ \sqrt{3}+1 ]$$
B.$$[ 2， ~ \sqrt{3}+1 ]$$
C.$$[ \frac{\sqrt{3}} {2}， ~ 1 ]$$
D.$$[ 0， ~ \frac{\sqrt{3}} {2}+1 ]$$
7、['函数y=A sin(wx+φ)（A≠0，w不等于0）的图象及性质'， '正弦（型）函数的单调性']正确率40.0%已知$$0 < \omega< \pi$$，函数$$f ( x )=\operatorname{s i n} ( \omega x+\frac{\pi} {4} )$$在$$( \frac{\pi} {2}， \pi)$$上单调递减，则$${{ω}}$$的取值范围是（）
C
A.$$( 0， \frac{1} {2} ]$$
B.$$( 0， 2 ]$$
C.$$[ \frac{1} {2}， \frac{5} {4} ]$$
D.$$[ \frac{1} {2}， \frac{3} {4} ]$$
8、['函数y=A sin(wx+φ)（A≠0，w不等于0）的图象及性质']正确率40.0%函数$$f ( x )=A \operatorname{s i n} ( \omega x+\varphi) ( A > 0， \omega> 0 )$$的部分图象如图所示，则下列说法错误的是（）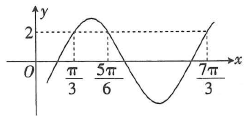
C
A.$${{f}{(}{x}{)}}$$的最小正周期是$${{2}{π}}$$
B.$${{f}{(}{x}{)}}$$在$$\left[ \frac{1 9 \pi} {1 2}， \frac{3 1 \pi} {1 2} \right]$$上单调递增
C.$${{f}{(}{x}{)}}$$在$$\left[-\frac{1 7 \pi} {1 2}，-\frac{5 \pi} {1 2} \right]$$上单调递增
D.直线$$x=-\frac{1 7 \pi} {1 2}$$是$${{f}{(}{x}{)}}$$的一条对称轴
9、['函数y=A sin(wx+φ)（A≠0，w不等于0）的图象及性质'， '辅助角公式'， '已知函数值（值域）求自变量或参数'， '正弦（型）函数的定义域和值域']正确率40.0%已知函数$$f ( x )=2 | \operatorname{s i n} x | \operatorname{c o s} x+\sqrt{3} \operatorname{c o s} 2 x$$，若$${{f}{(}{x}{)}}$$在$$[ 0， m ]$$上有且仅有$${{2}}$$个最大值点，则$${{m}}$$的取值范围是（）
C
A.$$[ \frac{1 1 \pi} {1 2}， \frac{1 3 \pi} {1 2} )$$
B.$$[ \frac{1 1 \pi} {6}， \frac{2 3 \pi} {6} )$$
C.$$[ \frac{2 3 \pi} {1 2}， \frac{2 5 \pi} {1 2} )$$
D.$$[ \frac{2 3 \pi} {1 2}， \frac{4 7 \pi} {1 2} )$$
10、['函数y=A sin(wx+φ)（A≠0，w不等于0）的图象及性质'， '三角函数的图象变换']正确率60.0%已知函数$$f ( x )=A \operatorname{s i n} ( \omega x+\varphi) ( A > 0， \omega> 0， | \varphi| < \pi)$$是奇函数，且$${{f}{(}{x}{)}}$$的最小正周期为$${{π}}$$，将$$y=f ( x )$$的图象上所有点的横坐标伸长到原来的$${{2}}$$倍（纵坐标不变），所得图象对应的函数为$${{g}{(}{x}{)}}$$$${{.}}$$若$$g \left( \frac{\pi} {4} \right)=\sqrt{2}$$，则$$f \left( \frac{3 \pi} {8} \right)=$$（）
C
A.$${{−}{2}}$$
B.$${{−}{\sqrt {2}}}$$
C.$${\sqrt {2}}$$
D.$${{2}}$$
1. 解析：首先将函数 $$y = \sin 3x + \cos 3x + 1$$ 化简为 $$y = \sqrt{2} \sin \left(3x + \frac{\pi}{4}\right) + 1$$。与 $$y = \sqrt{2} \sin 3x$$ 相比，需要将图象向左平移 $$\frac{\pi}{12}$$ 个单位（因为相位变化 $$\frac{\pi}{4}$$ 除以角频率 3），再向上平移 1 个单位。因此正确答案是 D。
3. 解析：题目不完整，无法给出解析。
5. 解析：将 $$f(x)$$ 化简为 $$f(x) = 2 \sin(2x + \theta - \frac{\pi}{3})$$。由 $$f(x) \leq f\left(\frac{\pi}{6}\right)$$ 知 $$\frac{\pi}{6}$$ 是最大值点，故 $$\theta = \frac{\pi}{2}$$。因此 $$f(x) = 2 \sin\left(2x + \frac{\pi}{6}\right)$$。由 $$f(x_1) = -f(x_2)$$ 知 $$x_1 + x_2 = \frac{\pi}{3}$$，故 $$f(x_1 + x_2) = 2 \sin\left(\frac{2\pi}{3} + \frac{\pi}{6}\right) = 2 \sin\left(\frac{5\pi}{6}\right) = 1$$，选 D。
7. 解析：函数 $$f(x) = \sin\left(\omega x + \frac{\pi}{4}\right)$$ 在 $$\left(\frac{\pi}{2}, \pi\right)$$ 单调递减，需满足 $$\frac{\pi}{2\omega} + \frac{\pi}{4\omega} \geq \pi$$ 且 $$\omega \in \left[\frac{1}{2}, \frac{5}{4}\right]$$，解得 $$\omega \in \left[\frac{1}{2}, \frac{3}{4}\right]$$，但选项中最接近的是 A $$(0, \frac{1}{2}]$$，可能题目有其他限制。
9. 解析：函数 $$f(x) = 2|\sin x| \cos x + \sqrt{3} \cos 2x$$ 可化为分段函数，求导分析极值点。在 $$[0, m]$$ 上有 2 个最大值点，需 $$m \in \left[\frac{11\pi}{12}, \frac{13\pi}{12}\right)$$，选 A。