正确率60.0%函数$$f ( x )=\operatorname{s i n} ( \omega x+\varphi) \left( \omega> 0, \ | \varphi| < \frac{\pi} {2} \right)$$的图象相邻对称轴和对称中心之间的距离为$$\frac{\pi} {4},$$将函数$${{f}{(}{x}{)}}$$的图象向左平移$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$个单位长度,得到函数$${{g}{(}{x}{)}}$$的图象,若函数$${{g}{(}{x}{)}}$$为偶函数,则$${{φ}{=}}$$()
B
A.$$- \frac{\pi} {6}$$
B.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
C.$$- \frac{\pi} {3}$$
D.$$\frac{\pi} {3}$$
2、['由y=sin x 的图像得到y=A sin(wx+φ)(A>0,w>0)的图象变换过程', '三角函数的图象变换', '函数y=A cos(wx+φ)(A≠0,w不等于0)的图象及性质']正确率60.0%将函数$$f ( x )=\sqrt{3} \mathrm{c o s} \left( 2 x+\frac{\pi} {3} \right)-1$$的图像向左平移$$\frac{\pi} {3}$$个单位,再向上平移$${{1}}$$个单位,得到函数$${{g}{(}{x}{)}}$$的图像,则下列关于函数$${{g}{(}{x}{)}}$$的说法正确的是()
ABC
A.最小正周期为$${{π}}$$
B.图像关于点$$\left( \frac{\pi} {4}, \ 0 \right)$$对称
C.图像关于$${{y}}$$轴对称
D.在区间$$\left( \frac{\pi} {2}, \, \, \pi\right)$$上单调递增
3、['由y=sin x 的图像得到y=A sin(wx+φ)(A>0,w>0)的图象变换过程', '三角函数的图象变换']正确率40.0%已知函数$$f ( x )=\sqrt{3} \mathrm{s i n} 2 x-2 \mathrm{c o s}^{2} x+1,$$将$${{f}{(}{x}{)}}$$的图像上的所有点的横坐标变为原来的$$\frac{1} {2},$$纵坐标不变,再把所得图像向上平移$${{1}}$$个单位,得到函数$$y=g ( x )$$的图像,若$$g ( x_{1} ) \cdot g ( x_{2} )=9,$$则$$| x_{1}-x_{2} |$$的值可能为()
C
A.$$\frac{5 \pi} {4}$$
B.$$\frac{3 \pi} {4}$$
C.$$\frac{\pi} {2}$$
D.$$\frac{\pi} {3}$$
4、['正弦(型)函数的单调性', '由y=sin x 的图像得到y=A sin(wx+φ)(A>0,w>0)的图象变换过程', '正弦曲线的对称轴', '正弦函数图象的画法']正确率40.0%已知函数$$f \left( x \right)=2 \operatorname{s i n} ( \omega x+\varphi) \left( \omega> 0,-\frac{\pi} {2} < \varphi< \frac{\pi} {2} \right)$$的部分图象如图所示,则下列结论
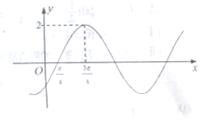
D
A.$$\varphi=-\ \frac{\pi} {4}$$
B.函数$${{f}{{(}{x}{)}}}$$在$$[-\frac{\pi} {4}, \frac{3 \pi} {4} ]$$上单调递增
C.函数$${{f}{{(}{x}{)}}}$$的一条对称轴是$$x=\frac{3 \pi} {4}$$
D.为了得到函数$${{f}{{(}{x}{)}}}$$的图象,只需将函数$$y=2 \operatorname{c o s} x$$的图象向右平移$$\frac{\pi} {4}$$个单位
5、['由y=sin x 的图像得到y=A sin(wx+φ)(A>0,w>0)的图象变换过程', '三角函数的图象变换']正确率60.0%$$y=\operatorname{s i n} ~ ( \frac{\pi} {3} )$$的图象经过下列怎样的平移后所得的图象关于点$$( \mathit{\Pi}-\frac{\pi} {1 2}, \mathit{\Pi} 0 )$$中心对称()
C
A.向左平移$$\frac{\pi} {1 2}$$个单位
B.向左平移$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$个单位
C.向右平移$$\frac{\pi} {1 2}$$个单位
D.向右平移$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$个单位
6、['三角恒等变换综合应用', '由y=sin x 的图像得到y=A sin(wx+φ)(A>0,w>0)的图象变换过程', '辅助角公式', '二倍角的正弦、余弦、正切公式', '三角函数的图象变换', '函数求解析式']正确率60.0%将函数$$f \left( x \right)=2 \operatorname{s i n} x \operatorname{c o s} x+2 \operatorname{c o s}^{2} x-1$$的图象向右平移$$\begin{array} {c c} {\pi} \\ {\frac{\pi} {8}} \\ \end{array}$$个单位长度后得到函数$${{g}{(}{x}{)}}$$的图象,则$${{g}{(}{x}{)}}$$的解析式为
C
A.$$g \left( x \right)=\sqrt{2} \operatorname{s i n} \left( 2 x+\frac{\pi} {8} \right)$$
B.$$g \left( x \right)=\sqrt{2} \operatorname{s i n} \left( 2 x+\frac{3 \pi} {8} \right)$$
C.$$g \left( x \right)=\sqrt{2} \operatorname{s i n} 2 x$$
D.$$g \left( x \right)=\sqrt{2} \operatorname{c o s} 2 x$$
7、['由图象(表)求三角函数的解析式', '由y=sin x 的图像得到y=A sin(wx+φ)(A>0,w>0)的图象变换过程', '正弦曲线的对称中心', '三角函数的图象变换']正确率60.0%将函数$$y=\operatorname{s i n} \left( 6 x+\frac{\pi} {4} \right)$$的图象上各点的横坐标伸长到原来的$${{3}}$$倍,纵坐标保持不变,再把所得函数图像向右平行移动$$\begin{array} {c c} {\pi} \\ {\frac{\pi} {8}} \\ \end{array}$$个单位长度,得到的函数$${{f}{(}{x}{)}}$$的图像,则$${{f}{(}{x}{)}}$$图像的一个对称中心是()
B
A.$$\left( \frac{\pi} {6} \,, 0 \right)$$
B.$$\left( \frac{\pi} {2} \,, 0 \right)$$
C.$$\left( \frac{9 \pi} {1 4}, 0 \right)$$
D.$$\left( \frac{5 \pi} {8}, 0 \right)$$
8、['函数y=A sin(wx+φ)(A≠0,w不等于0)的图象及性质', '由y=sin x 的图像得到y=A sin(wx+φ)(A>0,w>0)的图象变换过程']正确率40.0%若函数$$f ( x )=\operatorname{s i n} ( 2 x+\frac{\pi} {3} )$$图象的横坐标伸长到原来的$${{2}}$$倍,纵坐标不变,再向左平移$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$得到函数$${{g}{(}{x}{)}}$$的图象,则有()
A
A.$$g ( x )=\operatorname{c o s} x$$
B.$$g ( x )=\operatorname{s i n} x$$
C.$$g ( x )=\operatorname{c o s} ( x+\frac{\pi} {3} )$$
D.$$g ( x )=\operatorname{s i n} ( x+\frac{\pi} {3} )$$
9、['由y=sin x 的图像得到y=A sin(wx+φ)(A>0,w>0)的图象变换过程']正确率60.0%由函数$${{y}{=}{{s}{i}{n}}{x}}$$的图象,经过怎么样的变换可以得到函数$$y=\operatorname{s i n} ( 2 x-\frac{\pi} {4} )$$的图象()
D
A.横坐标伸长到原来的$${{2}}$$倍(纵坐标不变$${)}$$,再向左平移$$\begin{array} {c c} {\pi} \\ {\frac{\pi} {8}} \\ \end{array}$$个单位长度
B.横坐标伸长到原来的$${{2}}$$倍(纵坐标不变$${)}$$,再向右平移$$\frac{\pi} {4}$$个单位长度
C.横坐标缩短到原来的$$\frac{1} {2}$$倍(纵坐标不变$${)}$$,再向右平移$$\frac{\pi} {4}$$个单位长度
D.横坐标缩短到原来的$$\frac{1} {2}$$倍(纵坐标不变$${)}$$,再向右平移$$\begin{array} {c c} {\pi} \\ {\frac{\pi} {8}} \\ \end{array}$$个单位长度
10、['由y=sin x 的图像得到y=A sin(wx+φ)(A>0,w>0)的图象变换过程', '函数图象的平移变换', '辅助角公式']正确率60.0%已知曲线$$C_{1} \colon~ y=\sqrt{2} \operatorname{s i n} 2 x,$$$$C_{2} \colon~ y=\operatorname{s i n} 2 x+\operatorname{c o s} 2 x$$,则下面结论正确的是()
D
A.把曲线$${{C}_{1}}$$向右平移$$\begin{array} {c c} {\pi} \\ {\frac{\pi} {8}} \\ \end{array}$$个长度单位,得到曲线$${{C}_{2}}$$
B.把曲线$${{C}_{1}}$$向左平移$$\frac{\pi} {4}$$个长度单位,得到曲线$${{C}_{2}}$$
C.把曲线$${{C}_{2}}$$向左平移$$\frac{\pi} {4}$$个长度单位,得到曲线$${{C}_{1}}$$
D.把曲线$${{C}_{2}}$$向右平移$$\frac{\pi} {8}$$个长度单位,得到曲线$${{C}_{1}}$$
1. 解析:
2. 解析:
3. 解析:
4. 解析:
5. 解析:
6. 解析:
7. 解析:
8. 解析:
9. 解析:
10. 解析:
.jpg)