正确率80.0%扇形的半径为$${{1}}$$,圆心角的弧度数为$${{2}}$$,则这个扇形的周长是$${{(}{)}}$$
A.$${{3}}$$
B.$${{4}}$$
C.$${{5}}$$
D.以上都不对
2、['扇形弧长公式', '三角函数中的数学文化']正确率60.0%我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”现有一类似问题,不确定大小的圆柱形木材部分埋在墙壁中,其截面如图所示.用锯去锯此圆柱形木材,若锯口深$$C D=\sqrt{2}-1,$$锯道长$$A B=2,$$则图中$${{A}{C}{B}^{⌢}}$$的长度为()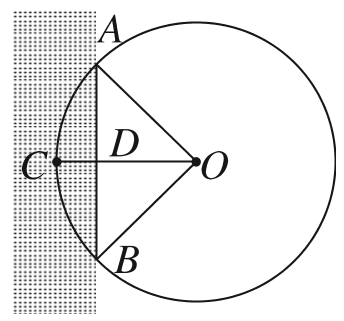
B
A.$$\frac{\pi} {2}$$
B.$$\frac{\sqrt{2}} {2} \pi$$
C.$${{π}}$$
D.$${\sqrt {2}{π}}$$
3、['扇形弧长公式', '角α与π/2±α的三角函数值之间的关系', '三角函数中的数学文化']正确率60.0%刘徽是中国魏晋时期杰出的数学家,他提出“割圆求周”方法:当$${{n}}$$很大时,用圆内接正$${{n}}$$边形的周长近似等于圆周长,并计算出精确度很高的圆周率$$\pi\approx3. 1 4 1 \; 6$$.在《九章算术注》中总结出“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”的极限思想,可以说他是中国古代极限思想的杰出代表.运用此思想,当$${{π}}$$取$$3. 1 4 1 6$$时可得$${{c}{o}{s}{{8}{9}^{∘}}}$$的近似值为()
B
A.$$0. 0 0 8 \, 7 3$$
B.$$0. 0 1 7 \, 4 5$$
C.$$0. 0 2 6 \; 1 8$$
D.$$0. 0 3 4 \; 9 1$$
4、['扇形弧长公式', '圆的定义与标准方程']正确率60.0%已知圆$${{C}}$$关于$${{y}}$$轴对称,经过点$$( 1, 0 )$$且被$${{x}}$$轴分成两段,弧长比为$${{1}}$$∶$${{2}{,}}$$则圆$${{C}}$$的方程为()
A
A.$$x^{2}+\left( y+\frac{\sqrt{3}} {3} \right)^{2}=\frac{4} {3}$$或$$x^{2}+\left( y-\frac{\sqrt{3}} {3} \right)^{2}=\frac{4} {3}$$
B.$$x^{2}+\left( y-\frac{\sqrt{3}} {3} \right)^{2}=\frac{4} {3}$$或$$( x-\sqrt{3} )^{2}+y^{2}=\frac4 3$$
C.$$( x-\sqrt{3} )^{2}+y^{2}=\frac4 3$$或$$x^{2}+\left( y+\frac{\sqrt{3}} {3} \right)^{2}=\frac{4} {3}$$
D.$$( x+\sqrt{3} )^{2}+y^{2}=\frac4 3$$或$$( x-\sqrt{3} )^{2}+y^{2}=\frac4 3$$
5、['扇形弧长公式']正确率60.0%若一圆弧的长等于其所在圆的内接正三角形的边长,那么其圆心角的弧度数是()
C
A.$$\frac{\pi} {3}$$
B.$$\frac{2 \pi} {3}$$
C.$${\sqrt {3}}$$
D.$${{2}}$$
6、['扇形弧长公式', '弧长公式及扇形面积公式的两种表示']正确率60.0%在单位圆中,大小为$${{1}{0}{5}^{∘}}$$的圆心角所对弧的长度为()
D
A.$$\frac{\pi} {1 2}$$
B.$$\frac{\pi} {4}$$
C.$$\frac{5 \pi} {1 2}$$
D.$$\frac{7 \pi} {1 2}$$
7、['扇形弧长公式']正确率60.0%在半径为$${{1}{0}}$$的圆中,$${{2}{4}{0}^{∘}}$$的圆心角所对的弧长为()
A
A.$$\frac{4 0} {3} \pi$$
B.$$\frac{2 0} {3} \pi$$
C.$$\frac{2 0 0} {3} \pi$$
D.$$\frac{4 0 0} {3} \pi$$
8、['扇形弧长公式']正确率80.0%已知半径为$${{2}}$$的圆上,有一条弧的长是$${{2}}$$,则该弧所对的圆心角(正角)的弧度数为()
D
A.$${{4}}$$
B.$${{3}}$$
C.$${{2}}$$
D.$${{1}}$$
9、['扇形弧长公式', '扇形面积公式']正确率80.0%已知扇形的面积为$${{4}}$$,弧长为$${{4}}$$,求这个扇形的圆心角是()
C
A.$${{4}}$$
B.$${{2}^{∘}}$$
C.$${{2}}$$
D.$${{4}^{∘}}$$
10、['扇形弧长公式', '棱柱的结构特征及其性质']正确率40.0%已知正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{2}}$$,一只蚂蚁在该正方体的表面上爬行,在爬行过程中,到点$${{A}}$$的直线距离恒为$${{2}{\sqrt {2}}}$$,它爬行的轨迹是一个封闭的曲线,则曲线的长度是$${{(}{)}}$$
D
A.$${{3}{\sqrt {2}}}$$
B.$${{6}{\sqrt {2}}}$$
C.$${{2}{π}}$$
D.$${{3}{π}}$$
1. 扇形周长由两条半径和弧长组成。弧长公式为 $$l = r \theta$$,其中 $$r = 1$$,$$\theta = 2$$,所以弧长 $$l = 2$$。两条半径总长为 $$2 \times 1 = 2$$,因此周长为 $$2 + 2 = 4$$。答案为 $$B$$。
2. 设圆的半径为 $$r$$,由垂径定理得 $$(r - (\sqrt{2} - 1))^2 + 1^2 = r^2$$,解得 $$r = \sqrt{2}$$。圆心角 $$\theta$$ 满足 $$\sin \frac{\theta}{2} = \frac{1}{\sqrt{2}}$$,即 $$\theta = \frac{\pi}{2}$$。弧长 $$l = r \theta = \sqrt{2} \times \frac{\pi}{2} = \frac{\sqrt{2}}{2} \pi$$。答案为 $$B$$。
3. 利用极限思想,当 $$n$$ 很大时,正 $$n$$ 边形逼近圆。设单位圆内接正 $$n$$ 边形边长 $$L_n = 2 \sin \frac{\pi}{n}$$,圆周长为 $$2\pi$$。当 $$n = 360$$ 时,$$L_{360} \approx 2\pi / 360 = \pi / 180$$。对于 $$89^\circ$$,$$\cos 89^\circ = \sin 1^\circ \approx \frac{\pi}{180} \approx 0.01745$$。答案为 $$B$$。
4. 圆关于 $$y$$ 轴对称,设圆心为 $$(0, b)$$。圆经过 $$(1, 0)$$,则半径 $$r = \sqrt{1 + b^2}$$。被 $$x$$ 轴分成弧长比 $$1:2$$,说明圆心角为 $$120^\circ$$ 和 $$240^\circ$$。由几何关系得 $$|b| = \frac{\sqrt{3}}{3} r$$,代入解得 $$b = \pm \frac{\sqrt{3}}{3}$$,$$r = \frac{2\sqrt{3}}{3}$$。圆方程为 $$x^2 + \left(y \pm \frac{\sqrt{3}}{3}\right)^2 = \frac{4}{3}$$。答案为 $$A$$。
5. 圆内接正三角形边长为 $$r \sqrt{3}$$(其中 $$r$$ 为半径)。设圆弧长为 $$l = r \sqrt{3}$$,圆心角 $$\theta = \frac{l}{r} = \sqrt{3}$$。答案为 $$C$$。
6. 单位圆中弧长公式为 $$l = \theta$$($$\theta$$ 为弧度)。$$105^\circ = \frac{105 \pi}{180} = \frac{7\pi}{12}$$。答案为 $$D$$。
7. 弧长公式为 $$l = r \theta$$,其中 $$\theta = 240^\circ = \frac{4\pi}{3}$$,$$r = 10$$,所以 $$l = 10 \times \frac{4\pi}{3} = \frac{40\pi}{3}$$。答案为 $$A$$。
8. 弧长公式为 $$l = r \theta$$,已知 $$l = 2$$,$$r = 2$$,解得 $$\theta = 1$$。答案为 $$D$$。
9. 扇形面积公式为 $$A = \frac{1}{2} r l$$,已知 $$A = 4$$,$$l = 4$$,解得 $$r = 2$$。圆心角 $$\theta = \frac{l}{r} = 2$$。答案为 $$C$$。
10. 蚂蚁轨迹为以 $$A$$ 为球心、半径为 $$2\sqrt{2}$$ 的球与正方体表面的交线。计算得轨迹为三个四分之一圆弧,总长度为 $$3 \times \frac{\pi}{2} \times 2\sqrt{2} = 3\pi$$。答案为 $$D$$。
.jpg)