.jpg)
正确率80.0%扇形的半径为$${{1}}$$，圆心角的弧度数为$${{2}}$$，则这个扇形的周长是$${{(}{)}}$$
A.$${{3}}$$
B.$${{4}}$$
C.$${{5}}$$
D.以上都不对
2、['弧长公式及扇形面积公式的两种表示']正确率80.0%设扇形的周长为$${{8}{c}{m}}$$，面积为$${{4}{c}{{m}^{2}}}$$，则扇形的圆心角的弧度数是$${{(}{)}}$$
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
3、['弧长公式及扇形面积公式的两种表示']正确率80.0%若扇形的周长为$${{3}{6}}$$，要使这个扇形的面积最大，则此时扇形的圆心角$${{α}}$$的弧度为$${{(}{)}}$$
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
4、['弧长公式及扇形面积公式的两种表示']正确率80.0%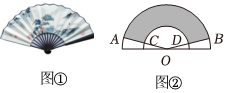
中国折叠扇有着深厚的文化底蕴$${{.}}$$如图②，在半圆$${{O}}$$中作出两个扇形$${{O}{A}{B}}$$和$${{O}{C}{D}}$$，用扇环形$$A B D C ($$图中阴影部分$${{)}}$$制作折叠扇的扇面$${{.}}$$记扇环形$${{A}{B}{D}{C}}$$的面积为$${{S}_{1}}$$，扇形$${{O}{A}{B}}$$的面积为$${{S}_{2}}$$，当$${{S}_{1}}$$与$${{S}_{2}}$$的比值为$$\frac{{\sqrt5}-1} {2}$$时，扇面的形状较为美观，则此时扇形$${{O}{C}{D}}$$的半径与半圆$${{O}}$$的半径之比为$${{(}{)}}$$
A.$$\frac{\sqrt{5}+1} {4}$$
B.$$\frac{{\sqrt5}-1} {2}$$
C.$${{3}{−}{\sqrt {5}}}$$
D.$$\sqrt{5}-2$$
5、['弧长公式及扇形面积公式的两种表示'， '圆锥的结构特征及其性质'， '圆柱、圆锥、圆台的侧面积与表面积']正确率40.0%圆锥的母线长为$${{4}}$$，侧面展开图为一个半圆，则该圆锥表面积为（）
B
A.$${{1}{0}{π}}$$
B.$${{1}{2}{π}}$$
C.$${{1}{6}{π}}$$
D.$${{1}{8}{π}}$$
6、['弧长公式及扇形面积公式的两种表示']正确率80.0%若一扇形的弧长为$${{2}{π}}$$，半径为$${{6}}$$，则该扇形所对的圆心角为$${{(}{)}}$$
C
A.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
B.$$\frac{\pi} {2}$$
C.$$\frac{\pi} {3}$$
D.$$\frac{2 \pi} {3}$$
7、['弧长公式及扇形面积公式的两种表示']正确率80.0%将表面积为36π的圆锥沿母线将其侧面展开，得到一个圆心角为$$\frac{2 \pi} {3}$$的扇形，则该圆锥的轴截面的面积为（ ）
A.18$${\sqrt {3}}$$
B.18$${\sqrt {2}}$$
C.12$${\sqrt {3}}$$
D.24$${\sqrt {3}}$$
8、['弧长公式及扇形面积公式的两种表示']正确率80.0%《九章算术》是我国古代数学成就的杰出代表，其中《方田》章有弧田面积计算问题，计算术曰：以弦乘矢，矢又自乘，并之，二而一$${{.}}$$其大意是，弧田面积计算公式为：弧田面积$$= \frac{1} {2} \cdot( \nparallel\times\ddag+\ddag\times\ddag)$$，弧田是由圆弧$${{(}}$$简称为弧田弧$${{)}}$$和以圆弧的两端为顶点的线段$${{(}}$$简称为弧田弦$${{)}}$$围成的平面图形，公式中“弦”指的是弧田弦的长，“矢”等于弧田弧所在圆的半径与圆心到弧田弦的距离之差$${{.}}$$现有一弧田，其弦长$${{A}{B}}$$等于$${{6}}$$米，其弧所在圆为圆$${{O}}$$，若用上述弧田面积计算公式算得该弧田的面积为$$\frac{7} {2}$$平方米，则$$\operatorname{c o s} \angle A O B=( \it{\phi} )$$
A
A.$$\frac{7} {2 5}$$
B.$$\frac{3} {2 5}$$
C.$$\frac{1 2} {2 5}$$
D.$$\frac2 {2 5}$$
9、['弧长公式及扇形面积公式的两种表示']正确率60.0%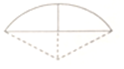
《九章算术》是我国古代数学成就的杰出代表作，其中《方田》章给出计算弧田面积所用的经验公式为：弧田面积$$= {\frac{1} {2}} ($$弦$${{+}}$$矢$${{)}{×}}$$矢，弧田$${{(}}$$如图$${{)}}$$由圆弧和其所对弦所围成，公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差现有圆心角为$$\frac{2 \pi} {3}$$，半径等于$${{2}{0}}$$米的弧田，按照上述经验公式计算所得弧田面积约是$${{(}{)}}$$
$${{(}}$$参考数据：$${{π}{≈}{{3}{.}{1}{4}}}$$，$$\sqrt3 \approx1. 7 3 )$$
C
A.$${{2}{2}{0}}$$平方米
B.$${{2}{4}{6}}$$平方米
C.$${{2}{2}{3}}$$平方米
D.$${{2}{5}{0}}$$平方米
10、['弧长公式及扇形面积公式的两种表示']正确率60.0%彝族图案作为人类社会发展的一种物质文化，有着灿烂历史$${{.}}$$按照图案的载体大致分为彝族服饰图案，彝族漆器图案，彝族银器图案等$${{.}}$$其中蕴含着丰富的数学文化，如图$${{1}}$$：漆器图案中出现的“阿基米德螺线”，该曲线是由一动点沿一条射线以等角速度转动所形成的轨迹$${{.}}$$这些螺线均匀分布，将其简化抽象为图$${{2}}$$所示，若$${{O}{A}}$$长为$${{2}}$$个单位，则$${{∠}{A}{O}{B}}$$所对应的弧长为$${{(}{)}}$$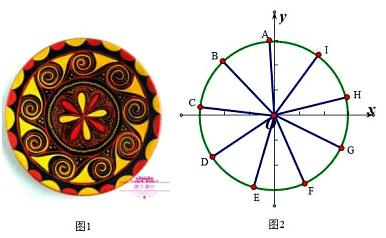
D
A.$$\frac{2 \pi} {9}$$
B.$$\frac{2 \pi} {3}$$
C.$$\frac{\sqrt{2} \pi} {3}$$
D.$$\frac{4 \pi} {9}$$
1. 扇形周长由两条半径和弧长组成。半径 $$r=1$$，圆心角 $$\theta=2$$，弧长 $$l=r\theta=2$$。因此周长 $$C=2r+l=2+2=4$$，选 $$B$$。
3. 设扇形半径为 $$r$$，弧长为 $$l$$，周长为 $$2r+l=36$$，面积 $$S=\frac{1}{2}rl$$。由 $$l=36-2r$$，代入得 $$S=-r^2+18r$$。当 $$r=9$$ 时 $$S$$ 最大，此时 $$\theta=\frac{l}{r}=\frac{18}{9}=2$$，选 $$B$$。
5. 圆锥侧面展开图半圆的弧长 $$l=4\pi$$，对应圆锥底面周长 $$2\pi r=4\pi$$，得 $$r=2$$。表面积 $$S=\pi r^2 + \frac{1}{2}\pi l^2/\pi=4\pi + 8\pi=12\pi$$，选 $$B$$。
7. 圆锥表面积 $$36\pi=\pi r^2 + \pi r l$$，展开扇形圆心角 $$\frac{2\pi}{3}=\frac{2\pi r}{l}$$，得 $$l=3r$$。代入得 $$r=3$$，$$l=9$$。圆锥高 $$h=\sqrt{l^2-r^2}=6\sqrt{2}$$，轴截面面积 $$\frac{1}{2}\times 2r \times h=18\sqrt{2}$$，选 $$B$$。
9. 圆心角 $$\frac{2\pi}{3}$$，弦长 $$2\times20\sin\frac{\pi}{3}=20\sqrt{3}$$，矢 $$20-20\cos\frac{\pi}{3}=10$$。面积 $$\frac{1}{2}(20\sqrt{3}+10)\times10\approx246$$ 平方米，选 $$B$$。