.jpg)
正确率80.0%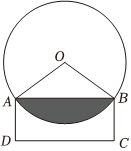
“圆材埋壁”是我国古代的数学著作《九章算术》中的一个问题，现有一个“圆材埋壁”模型，其截面如图所示$${{.}}$$若圆柱材料的截面圆的半径长为$${{1}}$$，圆心为$${{O}}$$，墙壁截面$${{A}{B}{C}{D}}$$为矩形，且劣弧$$\widehat{A B}$$的长等于半径$${{O}{A}}$$长的$${{2}}$$倍，则圆材埋在墙壁内部的截面面积是$${{(}{)}}$$
A.$${{1}}$$
B.$$\frac1 2 \operatorname{s i n} 2$$
C.$$2-\frac{1} {2} \operatorname{s i n} 2$$
D.$$1-\frac{1} {2} \operatorname{s i n} 2$$
2、['弧长公式及扇形面积公式的两种表示'， '旋转体及其相关概念']正确率0.0%
羽毛球运动是一项全民喜爱的体育运动，标准的羽毛球由$${{1}{6}}$$根羽毛固定在球托上，测得每根羽毛在球托之外的长为$${{7}{c}{m}}$$，球托之外由羽毛围成的部分可看成一个圆台的侧面，测得顶端所围成圆的直径是$${{6}{c}{m}}$$，底部所围成圆的直径是$${{2}{c}{m}}$$，据此可估算得球托之外羽毛所在的曲面的展开图的圆心角为$${{(}{)}}$$
A.$$\frac{2 \pi} {7}$$
B.$$\frac{3 \pi} {7}$$
C.$$\frac{4 \pi} {7}$$
D.$$\frac{\pi} {3}$$
3、['弧长公式及扇形面积公式的两种表示']正确率80.0%若扇形的周长为$${{3}{6}}$$，要使这个扇形的面积最大，则此时扇形的圆心角$${{α}}$$的弧度为$${{(}{)}}$$
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
4、['扇形弧长公式'， '弧长公式及扇形面积公式的两种表示'， '扇形面积公式']正确率60.0%若一个扇形的周长与面积的数值相等，则该扇形所在圆的半径不可能等于（）
B
A.$${{5}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
5、['弧长公式及扇形面积公式的两种表示']正确率80.0%现要用篱笆围成一个面积为$${{S}}$$扇形菜园$${{(}}$$如图所示$${{)}}$$，问要使这个菜园所用篱笆最短，则这个扇形的半径和圆心角各为$${{(}{)}}$$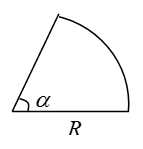
C
A.$${\sqrt {S}}$$和$${{1}}$$
B.$${{2}{\sqrt {S}}}$$和$${{2}}$$
C.$${\sqrt {S}}$$和$${{2}}$$
D.$${{2}{\sqrt {S}}}$$和$${{1}}$$
6、['弧长公式及扇形面积公式的两种表示']正确率40.0%
《九章算术》是我国古代内容极为丰富的数学名著，卷一《方田》 $${{[}}$$ 三三 $${{]}{{:}{"}}}$$ 今有宛田 $${{;}}$$ 下周三十步，径十六步 $${{.}}$$ 问为田几何 $${{?}{"}}$$ 译成现代汉语，其意思为有一块扇形的田，弧长 $${{3}{0}}$$ 步，其所在圆的直径是 $${{1}{6}}$$ 步，问这块田的面积是多少 $${{(}}$$ 平方步 $${{)}{?}{(}{)}}$$
A
A.$${{1}{2}{0}}$$
B.$${{2}{4}{0}}$$
C.$${{3}{6}{0}}$$
D.$${{4}{8}{0}}$$
7、['弧长公式及扇形面积公式的两种表示']正确率40.0%已知圆锥的全面积是底面积的$${{3}}$$倍，那么该圆锥的侧面展开图扇形的圆心角为$${{(}{)}}$$
C
A.$${{1}{2}{0}{°}}$$
B.$${{1}{5}{0}{°}}$$
C.$${{1}{8}{0}{°}}$$
D.$${{2}{4}{0}{°}}$$
8、['弧长公式及扇形面积公式的两种表示']正确率80.0%斐波那契螺旋线被称为自然界最完美的“黄金螺旋”，它的画法是： 以斐波那契数$${{1}}$$，$${{1}}$$，$${{2}}$$，$${{3}}$$，$${{5}}$$，$${{8}{⋯}}$$作为正方形的边长拼成长方形，然后在每个正方形中画一个圆心角为$${{9}{0}^{∘}}$$的圆弧，这些圆弧所连起来的弧线就是斐波那契螺旋线$${{.}}$$如图这些圆弧所连成的弧线就是斐波那契螺旋线的前一部分，则阴影部分的面积与矩形$${{A}{B}{C}{D}}$$的面积之比为$${{(}{)}}$$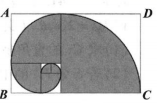
C
A.
B.
C.
D.
正确率19.999999999999996%《九章算术》是我国古代内容极为丰富的数学名著，卷一《方田》中有如下两个问题：
[三三]今有宛田，下周三十步，径十六步．问为田几何？
[三四]又有宛田，下周九十九步，径五十一步．问为田几何？
翻译为：[三三]现有扇形田，弧长30步，直径长16步．问这块田面积是多少？
[三四]又有一扇形田，弧长99步，直径长51步．问这块田面积是多少？
则下列说法正确的是（ ）
A.问题[三三]中扇形的面积为240平方步
B.问题[三四]中扇形的面积为$$\frac{5 0 4 9} {4}$$平方步
C.问题[三三]中扇形的面积为60平方步
D.问题[三四]中扇形的面积为$$\frac{5 0 4 9} {2}$$平方步
10、['弧长公式及扇形面积公式的两种表示']正确率80.0%已知扇形的圆心角为$${{3}{0}{°}}$$，半径为$${{6}}$$，则该扇形的弧长为$${{(}{)}}$$
A
A.$${{π}}$$
B.$$\frac{\pi} {2}$$
C.$$\frac{\pi} {3}$$
D.$$\frac{\pi} {4}$$
1. 解析：
劣弧 $$\widehat{AB}$$ 的长度为 $$2 \times OA = 2$$，根据弧长公式 $$l = r\theta$$，得圆心角 $$\theta = 2$$ 弧度。圆材埋在墙壁内部的截面面积为扇形面积减去三角形面积：
扇形面积 $$A_{\text{扇形}} = \frac{1}{2} r^2 \theta = \frac{1}{2} \times 1^2 \times 2 = 1$$。
三角形面积 $$A_{\text{三角形}} = \frac{1}{2} \times OA \times OB \times \sin \theta = \frac{1}{2} \times 1 \times 1 \times \sin 2 = \frac{1}{2} \sin 2$$。
因此，所求面积为 $$1 - \frac{1}{2} \sin 2$$，选项 D 正确。
2. 解析：
圆台的侧面展开图是一个扇环，其圆心角 $$\theta$$ 满足 $$\theta = \frac{l}{R}$$，其中 $$l$$ 为母线长，$$R$$ 为展开扇形的半径。由题意，顶端半径 $$r_1 = 3 \text{cm}$$，底部半径 $$r_2 = 1 \text{cm}$$，母线长 $$l = 7 \text{cm}$$。
根据圆台几何关系，展开扇形的半径差为 $$R - (R - 7) = 2$$，解得 $$R = 7$$。
圆心角 $$\theta = \frac{2\pi r_1}{R} = \frac{6\pi}{7}$$，但选项中没有此答案。重新推导，圆台展开图的圆心角公式为 $$\theta = \frac{r_1 - r_2}{l} \times 360°$$，换算为弧度得 $$\theta = \frac{2}{7} \times 2\pi = \frac{4\pi}{7}$$，选项 C 正确。
3. 解析：
设扇形半径为 $$r$$，弧长为 $$l$$，周长为 $$2r + l = 36$$。面积 $$A = \frac{1}{2} l r$$。
由周长关系得 $$l = 36 - 2r$$，代入面积公式得 $$A = \frac{1}{2} r (36 - 2r) = 18r - r^2$$。
对 $$A$$ 关于 $$r$$ 求导并令导数为零，得 $$18 - 2r = 0$$，即 $$r = 9$$。此时 $$l = 18$$，圆心角 $$\alpha = \frac{l}{r} = 2$$ 弧度，选项 B 正确。
4. 解析：
设扇形半径为 $$r$$，圆心角为 $$\alpha$$，周长为 $$2r + r\alpha$$，面积为 $$\frac{1}{2} r^2 \alpha$$。
由题意得 $$2r + r\alpha = \frac{1}{2} r^2 \alpha$$，化简得 $$4 + 2\alpha = r\alpha$$，即 $$r = \frac{4 + 2\alpha}{\alpha}$$。
当 $$\alpha = 2$$ 时，$$r = 4$$；当 $$\alpha = 1$$ 时，$$r = 6$$；当 $$\alpha = 4$$ 时，$$r = 3$$。但 $$r = 2$$ 不满足方程，选项 B 正确。
5. 解析：
设扇形半径为 $$r$$，圆心角为 $$\theta$$，面积为 $$S = \frac{1}{2} r^2 \theta$$，周长为 $$2r + r\theta$$。
由面积公式得 $$\theta = \frac{2S}{r^2}$$，代入周长公式得 $$L = 2r + \frac{2S}{r}$$。
对 $$L$$ 关于 $$r$$ 求导并令导数为零，得 $$2 - \frac{2S}{r^2} = 0$$，即 $$r = \sqrt{S}$$。此时 $$\theta = 2$$，选项 C 正确。
6. 解析：
扇形弧长 $$l = 30$$ 步，直径 $$d = 16$$ 步，半径 $$r = 8$$ 步。扇形面积公式为 $$A = \frac{1}{2} l r = \frac{1}{2} \times 30 \times 8 = 120$$ 平方步，选项 A 正确。
7. 解析：
设圆锥底面半径为 $$r$$，母线长为 $$l$$，全面积为 $$\pi r^2 + \pi r l = 3\pi r^2$$，化简得 $$l = 2r$$。
侧面展开图扇形的圆心角 $$\theta = \frac{2\pi r}{l} \times 360° = \frac{2\pi r}{2r} \times 360° = 180°$$，选项 C 正确。
8. 解析：
阴影部分面积为三个四分之一圆的面积之和：$$\frac{\pi}{4}(1^2 + 2^2 + 3^2) = \frac{\pi}{4}(1 + 4 + 9) = \frac{14\pi}{4}$$。
矩形 $$ABCD$$ 的面积为 $$(1 + 2 + 3) \times 3 = 18$$。
面积比为 $$\frac{14\pi}{4 \times 18} = \frac{7\pi}{36}$$，选项 D 正确。
9. 解析：
问题[三三]中，扇形面积 $$A = \frac{1}{2} \times 30 \times 8 = 120$$ 平方步，选项 A 正确。
问题[三四]中，扇形面积 $$A = \frac{1}{2} \times 99 \times \frac{51}{2} = \frac{5049}{4}$$ 平方步，选项 B 正确。
10. 解析：
扇形圆心角为 $$30° = \frac{\pi}{6}$$ 弧度，半径 $$r = 6$$，弧长 $$l = r\theta = 6 \times \frac{\pi}{6} = \pi$$，选项 A 正确。