正确率40.0%如图所示,在平面直角坐标系$${{x}{O}{y}}$$中,一单位圆的圆心的初始位置在($${{0}}$$,$${{1}}$$),此时圆上一点$${{P}}$$的位置在($${{0}}$$,$${{0}}$$),圆在$${{x}}$$轴上沿正向滚动,当圆滚动到圆心位于($${{2}}$$,$${{1}}$$)时,点$${{P}}$$的坐标为( )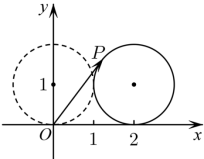
D
A.$$( 2-\operatorname{c o s} 2, 1-\operatorname{s i n} 2 )$$
B.$$( 1-\operatorname{s i n} 2, 2-\operatorname{c o s} 2 )$$
C.$$( 1-\operatorname{c o s} 2, 2-\operatorname{s i n} 2 )$$
D.$$( 2-\operatorname{s i n} 2, 1-\operatorname{c o s} 2 )$$
2、['扇形弧长公式', '圆的定义与标准方程']正确率60.0%已知圆$$O_{\colon} ~ x^{2}+y^{2}=1$$,一只蚂蚁从点$$A ( \frac{1} {2}, ~-\frac{\sqrt{3}} {2} )$$出发,沿圆周爬行(逆时针或顺时针),当它爬行到点$$B ~ ( ~-~ 1, ~ 0 )$$时,蚂蚁爬行的最短路程为()
A
A.$$\frac{2 \pi} {3}$$
B.$$\frac{5 \pi} {6}$$
C.$$\frac{4 \pi} {3}$$
D.$$\frac{7 \pi} {6}$$
3、['扇形弧长公式']正确率40.0%半径为$${{3}{c}{m}}$$,圆心角为$${{1}{2}{0}^{∘}}$$的扇形的弧长为()
A
A.$${{2}{π}{c}{m}}$$
B.$$\frac{2 \pi} {3} c m$$
C.$${\frac{4 \pi} {3}} c m$$
D.$${\frac{5 \pi} {3}} c m$$
4、['扇形弧长公式', '扇形面积公式']正确率60.0%已知扇形的周长是$${{1}{0}{{c}{m}}}$$,面积是$${{4}{c}{{m}^{2}}}$$,则扇形的圆心角$${{α}}$$的弧度数是()
B
A.$${{8}}$$
B.$$\frac{1} {2}$$
C.$${{8}}$$或$$\frac{1} {2}$$
D.$${{2}}$$
5、['扇形弧长公式', '圆柱、圆锥、圆台的侧面积与表面积', '旋转体的展开图']正确率60.0%已知圆锥的母线长为$${{3}}$$,其侧面展开图是圆心角为$${{1}{2}{0}^{∘}}$$的扇形,则该圆锥的侧面积为()
B
A.$${{2}{π}}$$
B.$${{3}{π}}$$
C.$${{4}{π}}$$
D.$${{6}{π}}$$
6、['扇形弧长公式', '扇形面积公式']正确率60.0%已知一扇形的半径为$${{2}}$$,弧长为$${{4}}$$,则此扇形的圆心角的弧度数和此扇形的面积分别为()
A
A.$${{2}{,}{4}}$$
B.$${{4}{,}{4}}$$
C.$${{2}{,}{8}}$$
D.$${{4}{,}{8}}$$
7、['扇形弧长公式', '扇形面积公式']正确率60.0%已知扇形$${{A}{O}{B}}$$的圆心角为$${{1}{2}{0}^{∘}}$$,半径长为$${{6}}$$,则扇形$${{A}{O}{B}}$$的面积是()
C
A.$${{9}{\sqrt {3}}}$$
B.$${{4}{π}}$$
C.$${{1}{2}{π}}$$
D.$${{2}{4}{π}}$$
8、['扇形弧长公式']正确率60.0%在半径为$${{1}}$$的圆中,$${{3}}$$弧度的圆心角所对的弧长为()
B
A.$${{3}{π}}$$
B.$${{3}}$$
C.$$\frac{3} {2} \pi$$
D.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
9、['扇形弧长公式', '弧度与角度的换算公式', '扇形面积公式']正确率60.0%已知圆心角为$${{1}{3}{5}^{∘}}$$的扇形的面积为$${{6}{π}}$$,则该扇形的弧长为()
A
A.$${{3}{π}}$$
B.$${\frac{3} {2}} \sqrt{2} \pi$$
C.$${{3}{\sqrt {2}}{π}}$$
D.$${{6}{π}}$$
10、['扇形弧长公式', '扇形面积公式']正确率60.0%已知扇形的周长为$${{9}}$$,圆心角为$${{1}}$$,则扇形的面积为$${{(}{)}}$$
C
A.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
B.$${{3}}$$
C.$$\frac{9} {2}$$
D.$${{9}}$$
1. 解析:圆滚动过程中,圆心从 $$(0,1)$$ 移动到 $$(2,1)$$,滚动的距离为 $$2$$,对应圆的弧长为 $$2$$。由于圆的半径为 $$1$$,滚动的角度为 $$2$$ 弧度。点 $$P$$ 的初始位置为 $$(0,0)$$,滚动后坐标为 $$(2-\sin 2, 1-\cos 2)$$。因此正确答案为 D。
2. 解析:圆 $$O$$ 的半径为 $$1$$,点 $$A$$ 的极角为 $$-60^\circ$$,点 $$B$$ 的极角为 $$180^\circ$$。顺时针爬行的路程为 $$|180^\circ - (-60^\circ)| = 240^\circ$$,对应弧长为 $$\frac{4\pi}{3}$$;逆时针爬行的路程为 $$120^\circ$$,对应弧长为 $$\frac{2\pi}{3}$$。最短路程为 $$\frac{2\pi}{3}$$,因此正确答案为 A。
3. 解析:扇形弧长公式为 $$l = r \theta$$,其中 $$\theta$$ 需转换为弧度。$$120^\circ = \frac{2\pi}{3}$$ 弧度,因此弧长为 $$3 \times \frac{2\pi}{3} = 2\pi$$ cm。正确答案为 A。
4. 解析:设扇形半径为 $$r$$,弧长为 $$l$$,则周长为 $$2r + l = 10$$,面积为 $$\frac{1}{2}rl = 4$$。解得 $$r = 1$$,$$l = 8$$ 或 $$r = 4$$,$$l = 2$$。圆心角 $$\alpha = \frac{l}{r}$$ 对应为 $$8$$ 或 $$\frac{1}{2}$$ 弧度。正确答案为 C。
5. 解析:圆锥侧面展开图是扇形,其弧长等于圆锥底面周长。设圆锥底面半径为 $$r$$,则 $$2\pi r = \frac{120^\circ}{360^\circ} \times 2\pi \times 3$$,解得 $$r = 1$$。侧面积为 $$\pi r l = \pi \times 1 \times 3 = 3\pi$$。正确答案为 B。
6. 解析:圆心角 $$\theta = \frac{l}{r} = \frac{4}{2} = 2$$ 弧度,扇形面积 $$A = \frac{1}{2}rl = \frac{1}{2} \times 2 \times 4 = 4$$。正确答案为 A。
7. 解析:扇形面积 $$A = \frac{120^\circ}{360^\circ} \times \pi \times 6^2 = \frac{1}{3} \times 36\pi = 12\pi$$。正确答案为 C。
8. 解析:弧长 $$l = r\theta = 1 \times 3 = 3$$。正确答案为 B。
9. 解析:设扇形半径为 $$r$$,面积为 $$\frac{135^\circ}{360^\circ} \times \pi r^2 = 6\pi$$,解得 $$r = 4$$。弧长为 $$\frac{135^\circ}{360^\circ} \times 2\pi \times 4 = 3\pi$$。正确答案为 A。
10. 解析:设扇形半径为 $$r$$,弧长为 $$l$$,则周长为 $$2r + l = 9$$,圆心角 $$\theta = \frac{l}{r} = 1$$,解得 $$r = 3$$,$$l = 3$$。面积为 $$\frac{1}{2}rl = \frac{1}{2} \times 3 \times 3 = \frac{9}{2}$$。正确答案为 C。
.jpg)