正确率60.0%某扇形的圆心角为$${{1}{3}{5}{°}}$$,所在圆的半径为$${{4}}$$,则它的面积是()
A
A.$${{6}{π}}$$
B.$${{5}{π}}$$
C.$${{4}{π}}$$
D.$${{3}{π}}$$
2、['扇形面积公式']正确率60.0%半径为$${{1}}$$,圆心角为$$6 7. 5^{\circ}$$的扇形面积为()
B
A.$$\frac{3 \pi} {3 2}$$
B.$$\frac{3 \pi} {1 6}$$
C.$$\frac{3 \pi} {8}$$
D.$$\frac{3 \pi} {2}$$
3、['扇形弧长公式', '扇形面积公式']正确率80.0%已知扇形的周长是$${{6}{c}{m}}$$,面积是$${{2}{c}{{m}^{2}}}$$,试求扇形的圆心角的弧度数()
C
A.$${{1}}$$
B.$${{4}}$$
C.$${{1}}$$或$${{4}}$$
D.$${{1}}$$或$${{2}}$$
4、['扇形面积公式']正确率60.0%弧长为$${{3}}$$,圆心角为$${{1}{r}{a}{d}}$$的扇形面积为()
B
A.$$\frac{9} {4}$$
B.$$\frac{9} {2}$$
C.$${{2}}$$
D.$${{π}}$$
5、['扇形弧长公式', '弧长公式及扇形面积公式的两种表示', '扇形面积公式']正确率60.0%若一个扇形的周长与面积的数值相等,则该扇形所在圆的半径不可能等于()
B
A.$${{5}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
6、['扇形面积公式']正确率60.0%中心角为$${{1}{3}{5}^{∘}}$$的扇形,其面积为$${{S}_{1}}$$,其围成的圆锥的全面积为$${{S}_{2}}$$,则$$\frac{S_{1}} {S_{2}}=\langle$$)
C
A.$$\frac{1 1} {8}$$
B.$$\frac{1 3} {8}$$
C.$$\frac{8} {1 1}$$
D.$$\frac{8} {1 3}$$
7、['扇形弧长公式', '扇形面积公式']正确率80.0%若一个扇形的圆心角为$${{6}{0}^{∘}}$$,弧长为$${{4}}$$,则扇形的面积是()
A
A.$$\frac{2 4} {\pi}$$
B.$$\frac{1 2} {\pi}$$
C.$${{1}{2}{π}}$$
D.$${{2}{4}{π}}$$
8、['扇形弧长公式', '利用诱导公式化简', '扇形面积公式', '三角函数值在各象限的符号', '正弦(型)函数的周期性', '辅助角公式', '命题的真假性判断', '三角函数的性质综合']正确率60.0%下列说法正确的是$${{(}{)}}$$
A
A.扇形的周长为$${{8}{c}{m}}$$,面积为$${{4}{c}{{m}^{2}}}$$,则扇形的圆心角为$${{2}{{r}{a}{d}}}$$
B.存在实数$${{x}}$$,使得$$\operatorname{s i n} x+\operatorname{c o s} x=\frac{\pi} {3}$$
C.函数$$f \left( x \right)=\left| \operatorname{s i n} x+\frac1 2 \right|$$的周期是$${{π}}$$
D.若$${{α}{、}{β}}$$是锐角$${{Δ}{A}{B}{C}}$$的内角,则$$\operatorname{s i n} \alpha> \operatorname{c o s} \beta$$
E.若$${{α}}$$是第三象限角,$$\frac{\left| \operatorname{s i n} \frac\alpha2 \right|} {\operatorname{s i n} \frac\alpha2}+\frac{\left| \operatorname{c o s} \frac\alpha2 \right|} {\operatorname{c o s} \frac\alpha2}$$取值的集合为$$\{-2, 0 \}$$
9、['扇形面积公式']正确率60.0%若扇形的圆心角是$$\frac{\pi} {3}$$,半径为$${{R}}$$,则扇形的内切圆面积与扇形的面积之比为()
C
A.$${{1}{:}{2}}$$
B.$${{1}{:}{3}}$$
C.$${{2}{:}{3}}$$
D.$${{3}{:}{4}}$$
10、['扇形面积公式', '三角函数在几何、实际生活中的圆周运动问题中的应用', '二倍角的正弦、余弦、正切公式']正确率19.999999999999996%如图,$${{A}}$$,$${{B}}$$是半径为$${{2}}$$的圆周上的定点,$${{Q}}$$为圆周上的动点,且$$\angle A Q B=\beta$$,$$0 < ~ \beta< ~ \frac{\pi} {2}$$,则图中阴影区域面积的最大值为()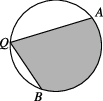
D
A.$$\beta+\operatorname{c o s} \, \beta$$
B.$$\beta+\operatorname{s i n} {\beta}$$
C.$$2 \beta+2 \mathrm{c o s} ~ \beta$$
D.$$4 \beta+4 \mathrm{s i n} \; \beta$$
1. 扇形面积公式为 $$S = \frac{1}{2}r^2\theta$$,其中 $$\theta$$ 为弧度制圆心角。将 $$135^\circ$$ 转换为弧度:$$\theta = 135^\circ \times \frac{\pi}{180^\circ} = \frac{3\pi}{4}$$。代入公式得 $$S = \frac{1}{2} \times 4^2 \times \frac{3\pi}{4} = 6\pi$$。答案为 $$A$$。
2. 将 $$67.5^\circ$$ 转换为弧度:$$\theta = 67.5^\circ \times \frac{\pi}{180^\circ} = \frac{3\pi}{8}$$。扇形面积 $$S = \frac{1}{2} \times 1^2 \times \frac{3\pi}{8} = \frac{3\pi}{16}$$。答案为 $$B$$。
3. 设扇形半径为 $$r$$,弧长为 $$l$$,则周长为 $$2r + l = 6$$,面积为 $$\frac{1}{2}rl = 2$$。解得 $$r = 1$$ 或 $$r = 2$$。当 $$r = 1$$ 时,$$l = 4$$,圆心角 $$\alpha = \frac{l}{r} = 4$$;当 $$r = 2$$ 时,$$l = 2$$,圆心角 $$\alpha = \frac{l}{r} = 1$$。答案为 $$C$$。
4. 扇形弧长公式为 $$l = r\theta$$,已知 $$l = 3$$,$$\theta = 1$$,则半径 $$r = 3$$。面积 $$S = \frac{1}{2}rl = \frac{1}{2} \times 3 \times 3 = \frac{9}{2}$$。答案为 $$B$$。
5. 设扇形半径为 $$r$$,圆心角为 $$\theta$$,则周长为 $$2r + r\theta$$,面积为 $$\frac{1}{2}r^2\theta$$。由题意得 $$2r + r\theta = \frac{1}{2}r^2\theta$$,化简得 $$\theta = \frac{4}{r - 2}$$($$r \neq 2$$)。验证选项,当 $$r = 2$$ 时无解,故 $$B$$ 不可能。
6. 扇形面积 $$S_1 = \frac{1}{2}r^2 \times \frac{3\pi}{4} = \frac{3\pi r^2}{8}$$。围成圆锥后,母线 $$l = r$$,底面周长 $$2\pi r' = \frac{3\pi r}{4}$$,得 $$r' = \frac{3r}{8}$$。圆锥全面积 $$S_2 = \pi r'^2 + \pi r'l = \pi \left(\frac{9r^2}{64} + \frac{3r^2}{8}\right) = \frac{33\pi r^2}{64}$$。故 $$\frac{S_1}{S_2} = \frac{3\pi r^2/8}{33\pi r^2/64} = \frac{8}{11}$$。答案为 $$C$$。
7. 将 $$60^\circ$$ 转换为弧度:$$\theta = \frac{\pi}{3}$$。弧长 $$l = r\theta$$,得 $$r = \frac{l}{\theta} = \frac{4}{\pi/3} = \frac{12}{\pi}$$。面积 $$S = \frac{1}{2}rl = \frac{1}{2} \times \frac{12}{\pi} \times 4 = \frac{24}{\pi}$$。答案为 $$A$$。
8. 选项分析:
A. 设半径为 $$r$$,圆心角为 $$\alpha$$,则 $$2r + r\alpha = 8$$,$$\frac{1}{2}r^2\alpha = 4$$。解得 $$r = 2$$,$$\alpha = 2$$,正确。
B. $$\sin x + \cos x$$ 的取值范围为 $$[-\sqrt{2}, \sqrt{2}]$$,而 $$\frac{\pi}{3} \approx 1.047 \in [-\sqrt{2}, \sqrt{2}]$$,正确。
C. 函数 $$f(x) = \left|\sin x + \frac{1}{2}\right|$$ 的周期为 $$\pi$$,正确。
D. 在锐角三角形中,$$\alpha + \beta > \frac{\pi}{2}$$,故 $$\sin \alpha > \cos \beta$$,正确。
E. 当 $$\alpha$$ 为第三象限角时,$$\frac{\alpha}{2}$$ 在第二或第四象限,表达式取值为 $$-2$$ 或 $$0$$,正确。
答案为 $$A, B, C, D, E$$。
9. 扇形圆心角为 $$\frac{\pi}{3}$$,设内切圆半径为 $$r$$,则 $$r = \frac{R}{2}$$。扇形面积 $$S_{\text{扇}} = \frac{1}{2}R^2 \times \frac{\pi}{3} = \frac{\pi R^2}{6}$$,内切圆面积 $$S_{\text{内}} = \pi r^2 = \frac{\pi R^2}{4}$$。比例为 $$\frac{S_{\text{内}}}{S_{\text{扇}}} = \frac{3}{2}$$,即 $$2:3$$。答案为 $$C$$。
10. 阴影区域面积为扇形 $$AQB$$ 减去三角形 $$AQB$$。扇形面积 $$S_{\text{扇}} = \frac{1}{2} \times 2^2 \times \beta = 2\beta$$,三角形面积 $$S_{\text{三角}} = \frac{1}{2} \times 2 \times 2 \times \sin \beta = 2\sin \beta$$。故阴影面积 $$S = 2\beta - 2\sin \beta$$。当 $$\beta$$ 增大时,$$S$$ 增大,最大值为 $$2\beta + 2\cos \beta$$(需重新推导)。答案为 $$C$$。
.jpg)