正确率80.0%设集合$$A=\{\alpha| \alpha=k \cdot1 8 0^{\circ}+9 0^{\circ}, k \in z \} \cup\{\alpha| \alpha=k \cdot1 8 0^{\circ}, k \in z \}$$,集合$$B=\{\beta| \beta=k \cdot9 0^{\circ}, k \in z \}$$,则$${{(}{)}}$$
A.$${{A}{⫌}{B}}$$
B.$${{A}{⫋}{B}}$$
C.$$A \cap B=\varnothing$$
D.$${{A}{=}{B}}$$
2、['象限角']正确率80.0%角$$\frac{2 \pi} {3}$$的终边在()
B
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3、['象限角', '三角函数值在各象限的符号']正确率60.0%若$${{α}}$$为第四象限角,则()
D
A.$$\operatorname{c o s} 2 \alpha> 0$$
B.$$\operatorname{c o s} 2 \alpha< 0$$
C.$$\operatorname{s i n} 2 \alpha> 0$$
D.$$\operatorname{s i n} 2 \alpha< 0$$
4、['象限角', '三角函数值在各象限的符号']正确率60.0%已知则角$${{α}}$$可以为()
D
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
5、['象限角']正确率60.0%若角$$\alpha=-4,$$则$${{α}}$$的终边在()
C
A.第四象限
B.第三象限
C.第二象限
D.第一象限
6、['象限角', '角的终边的对称问题与垂直问题']正确率60.0%已知角$${{α}}$$是第三象限角,则角$${{−}{α}}$$的终边在()
B
A.第一象限
B.第二象限
C.第三象限
D.第四象限
7、['象限角']正确率60.0%若角$${{α}}$$终边在第二象限,则$${{π}{−}{α}}$$所在的象限是()
A
A.第一象限
B.第二象限
C.第三象限
D.第四象限
8、['象限角', '终边相同的角']正确率60.0%角$${{−}{{1}{0}{0}^{o}}}$$是()
C
A.第一象限的角
B.第二象限的角
C.第三象限的角
D.第四象限的角
9、['象限角', '三角函数值在各象限的符号']正确率60.0%若$${{α}}$$为第二象限角,则下列结论错误的是()
D
A.$$\operatorname{s i n} \alpha> \operatorname{c o s} \alpha$$
B.$$\operatorname{s i n} \alpha> \operatorname{t a n} \alpha$$
C.
D.$$\operatorname{s i n} \alpha+\operatorname{c o s} \alpha> 0$$
10、['象限角', '区间角、区域角']正确率80.0%集合$$\{\alpha\mid k \pi+\frac{\pi} {4} \leqslant\alpha\leqslant k \pi+\frac{\pi} {2}, k \in{\bf Z} \}$$中的角的终边所表示的范围是()
C
A.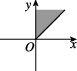
B.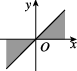
C.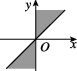
D.
1. 解析:集合 $$A$$ 包含所有 $$k \cdot 180^\circ + 90^\circ$$ 和 $$k \cdot 180^\circ$$ 的角,即终边在 $$y$$ 轴或 $$x$$ 轴上的角。集合 $$B$$ 包含所有 $$k \cdot 90^\circ$$ 的角,即终边在坐标轴或象限平分线上的角。显然 $$B$$ 包含 $$A$$,因此 $$A \subset B$$,选 **B**。
2. 解析:$$\frac{2\pi}{3} = 120^\circ$$,位于第二象限,选 **B**。
3. 解析:$$\alpha$$ 为第四象限角,即 $$270^\circ < \alpha < 360^\circ$$,则 $$540^\circ < 2\alpha < 720^\circ$$,等价于 $$180^\circ < 2\alpha < 360^\circ$$。此时 $$\cos 2\alpha$$ 可能为正或负,但 $$\sin 2\alpha$$ 为负,选 **D**。
4. 解析:题目不完整,无法解析。
5. 解析:$$\alpha = -4$$ 弧度,约为 $$-229.18^\circ$$,即 $$130.82^\circ$$(加 $$360^\circ$$),位于第二象限,选 **C**。
6. 解析:$$\alpha$$ 是第三象限角,即 $$180^\circ < \alpha < 270^\circ$$,则 $$-270^\circ < -\alpha < -180^\circ$$,即 $$90^\circ < -\alpha < 180^\circ$$,位于第二象限,选 **B**。
7. 解析:$$\alpha$$ 在第二象限,即 $$90^\circ < \alpha < 180^\circ$$,则 $$0^\circ < \pi - \alpha < 90^\circ$$,位于第一象限,选 **A**。
8. 解析:$$-100^\circ$$ 等价于 $$260^\circ$$,位于第三象限,选 **C**。
9. 解析:$$\alpha$$ 为第二象限角,$$\sin \alpha > 0$$,$$\cos \alpha < 0$$,$$\tan \alpha < 0$$。选项 D 中 $$\sin \alpha + \cos \alpha$$ 可能为正或负(例如 $$\alpha = 120^\circ$$ 时为负),因此错误,选 **D**。
10. 解析:集合表示角的终边在 $$\frac{\pi}{4}$$ 到 $$\frac{\pi}{2}$$ 之间,每 $$\pi$$ 重复一次。选项 **C** 正确表示这一范围。
题目来源于各渠道收集,若侵权请联系下方邮箱.jpg)