正确率60.0%如图,已知点$${{A}}$$是单位圆与$${{x}}$$轴正半轴的交点,角$${{α}}$$的终边与单位圆的交点为$$P, \, \, P M \perp x$$轴于点$${{M}{,}}$$过点$${{A}}$$作单位圆的切线交角$${{α}}$$的终边于点$${{T}{,}}$$则角$${{α}}$$的正弦线、余弦线、正切线分别是()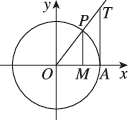
D
A.$$\overrightarrow{O M}, \, \, \overrightarrow{A T}, \, \, \overrightarrow{M P}$$
B.$$\overrightarrow{O M}, \, \, \overrightarrow{M P}, \, \, \overrightarrow{A T}$$
C.$$\overrightarrow{M P}, \, \, \overrightarrow{A T}, \, \, \overrightarrow{O M}$$
D.$$\overrightarrow{M P}, \, \, \overrightarrow{O M}, \, \, \overrightarrow{A T}$$
2、['正切线', '正弦线与余弦线']正确率60.0%已知$${{α}}$$是$${{△}{A}{B}{C}}$$的一个内角,且$$\mathrm{t a n} \alpha-\sqrt{3} \geqslant0,$$则$${{s}{i}{n}{α}}$$的取值范围是()
A
A.$$[ \frac{\sqrt{3}} {2}, ~ 1 \rgroup$$
B.$$[ \frac{1} {2}, 1 )$$
C.$$[ \frac{\sqrt{2}} {2}, \ \frac{\sqrt{3}} {2} ]$$
D.$$[ \frac{1} {2}, \ \frac{\sqrt{3}} {2} ]$$
3、['正切线', '正弦线与余弦线']正确率80.0%给出下列四个命题,其中正确的是()
D
A.当$${{α}}$$一定时,单位圆中的正弦线可以有两条
B.单位圆中,有相同正弦线的角相等
C.$${{α}}$$和$${{α}{+}{π}}$$有相同的正切线
D.具有相同正切线的两个角终边在同一条直线上
4、['正弦线与余弦线']正确率60.0%已知$$\mathrm{c o s} \alpha> \mathrm{c o s} \beta,$$那么下列说法正确的是()
D
A.若$${{α}{,}{β}}$$均是第一象限角,则$$\mathrm{s i n} \alpha> \mathrm{s i n} \beta$$
B.若$${{α}{,}{β}}$$均是第二象限角,则$$\mathrm{t a n} \alpha> \mathrm{t a n} \beta$$
C.若$${{α}{,}{β}}$$均是第三象限角,则$$\mathrm{s i n} \alpha> \mathrm{s i n} \beta$$
D.若$${{α}{,}{β}}$$均是第四象限角,则$$\mathrm{t a n} \alpha> \mathrm{t a n} \beta$$
5、['正弦线与余弦线']正确率60.0%若$$a=\mathrm{s i n} \frac{1 1 \pi} {1 2}, \, \, \, b=\mathrm{c o s} \frac{1 1 \pi} {1 2},$$则()
B
A.$$a < b < 0$$
B.$$b < 0 < a$$
C.$$b < a < 0$$
D.$$a < 0 < b$$
6、['同角三角函数的商数关系', '正弦线与余弦线']正确率60.0%已知角$${{α}}$$的正弦线和余弦线长度相等,且$${{α}}$$的终边在第三象限,则$${{t}{a}{n}{α}}$$等于()
B
A.$${{0}}$$
B.$${{1}}$$
C.$${{−}{1}}$$
D.$${\sqrt {3}}$$
7、['三角函数值在各象限的符号', '正弦线与余弦线']正确率40.0%点$$P ( \operatorname{s i n} 3-\operatorname{c o s} 3, \operatorname{s i n} 3+\operatorname{c o s} 3 )$$所在的象限为()
D
A.第一象限
B.第二象限
C.第三象限
D.第四象限
8、['正弦线与余弦线']正确率60.0%若角$$\alpha( 0 < \alpha< 2 \pi)$$的正弦线与余弦线互为相反数,那么$${{α}}$$的值为
D
A.$$\frac{\pi} {4}$$
B.$$\frac{3} {4} \pi$$
C.$$\frac{7} {4} \pi$$
D.$$\frac{3} {4} \pi$$或$$\frac{7} {4} \pi$$
9、['分段函数与方程、不等式问题', '正弦线与余弦线']正确率40.0%已知函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) \ =\left\{\begin{matrix} {-x^{2}-2 x ( x \geq0 )} \\ {x^{2}-2 x ( x < 0 )} \\ \end{matrix} \right.$$,又$${{α}{,}{β}}$$为锐角三角形两锐角则()
B
A.$$f ( \operatorname{s i n} \alpha) \ > f ( \operatorname{c o s} \beta)$$
B.$$f ( \operatorname{s i n} \alpha) ~ < f ( \operatorname{c o s} \beta)$$
C.$$f ( \operatorname{s i n} \alpha) \ > f ( \operatorname{s i n} \beta)$$
D.$$f \left( \begin{array} {l l} {\operatorname{c o s} \alpha} \\ \end{array} \right) > f \left( \begin{array} {l l} {\operatorname{c o s} \beta} \\ \end{array} \right)$$
10、['共线向量基本定理', '用角的终边上的点的坐标表示三角函数', '二倍角的正弦、余弦、正切公式', '正弦线与余弦线']正确率40.0%已知角$${{α}}$$的顶点为坐标原点,始边与$${{x}}$$轴的非负半轴重合,终边上有两点$$A ( 1, a )$$,$$B ( 2, b )$$,且$$\operatorname{c o s} 2 \alpha=\frac{2} {3}$$,则$$\vert a-b \vert=$$()
B
A.$$\frac{1} {5}$$
B.$$\frac{\sqrt{5}} {5}$$
C.$$\frac{2 \sqrt{5}} {5}$$
D.$${{1}}$$
1. 在单位圆中,点$$P$$的坐标为$$(\cos α, \sin α)$$。正弦线是$$P$$点到$$x$$轴的垂线,即$$\overrightarrow{MP}$$;余弦线是$$P$$点到$$y$$轴的垂线在$$x$$轴上的投影,即$$\overrightarrow{OM}$$;正切线是点$$T$$到$$A$$的向量,即$$\overrightarrow{AT}$$。因此答案为$$D$$。
2. 由$$\tan α \geq \sqrt{3}$$,得$$α \in \left[\frac{\pi}{3}, \frac{\pi}{2}\right)$$。在此区间内,$$\sin α$$单调递增,取值范围为$$\left[\frac{\sqrt{3}}{2}, 1\right)$$,但题目中$$α$$是三角形内角,最大值不超过$$\pi$$,因此$$\sin α \in \left[\frac{\sqrt{3}}{2}, 1\right)$$,答案为$$A$$。
3. 选项分析:
A. 单位圆中正弦线唯一,错误;
B. 相同正弦线的角可能互补,错误;
C. $$α$$和$$α+\pi$$的正切线相同,正确;
D. 相同正切线的角终边在同一直线或相差$$\pi$$,正确。
但题目要求选择“正确的是”,因此答案为$$C$$(若允许多选,$$C$$和$$D$$均正确,但单选题选$$C$$)。
4. 分析各选项:
A. 第一象限$$\cos α > \cos β$$说明$$α < β$$,但$$\sin α$$不一定大于$$\sin β$$,错误;
B. 第二象限$$\cos α > \cos β$$说明$$α < β$$,$$\tan α$$可能更小,错误;
C. 第三象限$$\cos α > \cos β$$说明$$α > β$$,$$\sin α$$更负,值更小,错误;
D. 第四象限$$\cos α > \cos β$$说明$$α < β$$,$$\tan α$$更大,正确。
答案为$$D$$。
5. 计算角度:$$\frac{11\pi}{12} = \pi - \frac{\pi}{12}$$。
$$a = \sin \frac{11\pi}{12} = \sin \frac{\pi}{12} > 0$$;
$$b = \cos \frac{11\pi}{12} = -\cos \frac{\pi}{12} < 0$$。
显然$$b < 0 < a$$,答案为$$B$$。
6. 正弦线和余弦线长度相等,即$$|\sin α| = |\cos α|$$,结合$$α$$在第三象限,得$$\sin α = \cos α$$,即$$\tan α = 1$$。但第三象限中$$\sin α = \cos α = -\frac{\sqrt{2}}{2}$$,因此$$\tan α = 1$$,答案为$$B$$。
7. 判断$$3$$弧度在第二象限,$$\sin 3 > 0$$,$$\cos 3 < 0$$。
$$x = \sin 3 - \cos 3 > 0$$;
$$y = \sin 3 + \cos 3$$,因$$3 \in \left(\frac{\pi}{2}, \pi\right)$$,$$\sin 3 + \cos 3$$可能为正或负,需具体计算:
$$\sin 3 \approx 0.141$$,$$\cos 3 \approx -0.990$$,故$$y \approx -0.849 < 0$$。
点$$P$$在第四象限,答案为$$D$$。
8. 正弦线与余弦线互为相反数,即$$\sin α = -\cos α$$,解得$$\tan α = -1$$。
在$$(0, 2\pi)$$内,$$α = \frac{3\pi}{4}$$或$$\frac{7\pi}{4}$$,答案为$$D$$。
9. 函数$$f(x)$$在$$x \geq 0$$时为$$-x^2 - 2x$$,在$$x < 0$$时为$$x^2 - 2x$$。
锐角三角形中,$$\alpha + \beta > \frac{\pi}{2}$$,故$$\sin \alpha > \cos \beta$$。
由于$$\sin \alpha$$和$$\cos \beta$$均在$$(0, 1)$$内,$$f(x)$$在$$[0, 1)$$单调递减,因此$$f(\sin \alpha) < f(\cos \beta)$$,答案为$$B$$。
10. 由$$A(1, a)$$和$$B(2, b)$$在终边上,得$$\tan α = a = \frac{b}{2}$$。
由$$\cos 2α = \frac{2}{3}$$,利用公式$$\cos 2α = \frac{1 - \tan^2 α}{1 + \tan^2 α}$$,解得$$\tan α = \pm \frac{\sqrt{5}}{5}$$。
因此$$|a - b| = |\tan α - 2\tan α| = |\tan α| = \frac{\sqrt{5}}{5}$$,答案为$$B$$。
.jpg)