正确率60.0%在平面直角坐标系$${{x}{O}{y}}$$中,以$${{O}}$$为圆心$${,{1}}$$为半径的圆上一点$${{P}}$$从点$$( 0, \ 1 )$$出发,按逆时针方向运动到达点$${{Q}{,}}$$若$$\widehat{P Q}=\frac{\pi} {6},$$则点$${{Q}}$$的坐标为()
A
A.$$\left(-\frac{1} {2}, \ \frac{\sqrt{3}} {2} \right)$$
B.$$\left( \frac{\sqrt{3}} {2}, \ \frac{1} {2} \right)$$
C.$$\left( \frac{1} {2}, ~ \frac{\sqrt{3}} {2} \right)$$
D.$$\left(-\frac{\sqrt{3}} {2}, \ \frac{1} {2} \right)$$
2、['利用单位圆定义任意角的三角函数', '用角的终边上的点的坐标表示三角函数', '两角和与差的余弦公式']正确率60.0%角$${{α}}$$的顶点在坐标原点,始边在$${{x}}$$轴非负半轴上,终边在第二象限,且与单位圆交点的纵坐标为$$\frac{1} {3},$$将其终边按逆时针方向旋转$${{3}{0}^{∘}}$$后与单位圆交点的横坐标是()
A
A.$$- \frac{1+2 \sqrt{6}} {6}$$
B.$$- \frac{\sqrt{3}+2 \sqrt{2}} {6}$$
C.$$\frac{2 \sqrt{6}-1} {6}$$
D.$$\frac{1-2 \sqrt{6}} {6}$$
3、['象限角', '利用单位圆定义任意角的三角函数', '不等式比较大小']正确率60.0%若$$\frac{\pi} {4}$$$${{<}{α}{<}}$$$$\frac{\pi} {2}$$,则点$$P ( \operatorname{c o s} \alpha-\operatorname{s i n} \alpha$$,$$\operatorname{s i n} \alpha-\operatorname{t a n} \alpha)$$位于 ( )
C
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4、['利用单位圆定义任意角的三角函数', '正弦线与余弦线']正确率60.0%若$${{M}{P}}$$和$${{O}{M}}$$分别是角$$\alpha=\frac{2 0 1 7 \pi} {2 0 1 8}$$的正弦线和余弦线,那么下列结论中正确的是()
D
A.$$M P < O M < 0$$
B.$$O M > 0 > M P$$
C.$$O M < M P < 0$$
D.$$M P > 0 > O M$$
5、['利用诱导公式化简', '利用单位圆定义任意角的三角函数']正确率60.0%设角$${{α}}$$的终边上有一点$$P ~ ( \mathrm{~-s i n ~ 2 5 ~^{\circ} ~, ~ \operatorname{c o s} ~ 2 5 ~}$$,则$${{α}}$$的一个可能值是()
C
A.65°
B.-65°
C.115°
D.155°
6、['利用单位圆定义任意角的三角函数', '用角的终边上的点的坐标表示三角函数']正确率60.0%若角$${{α}}$$的终边与单位圆的交点为$$P ( \frac{1 2} {1 3}, ~-\frac{5} {1 3} )$$,则)
B
A.$$\frac{5} {1 2}$$
B.$$- \frac{5} {1 2}$$
C.$$- \frac{1 2} {5}$$
D.$$\frac{1 2} {5}$$
7、['利用单位圆定义任意角的三角函数']正确率60.0%如果角$${{α}}$$的终边过点$$( 2 \operatorname{c o s} \frac{\pi} {6}, ~-2 \operatorname{s i n} \frac{\pi} {6} )$$,则$${{s}{i}{n}{α}}$$的值等于()
B
A.$$\frac{1} {2}$$
B.$$- \frac{1} {2}$$
C.$$\frac{\sqrt3} {2}$$
D.$$- \frac{\sqrt3} {2}$$
8、['利用单位圆定义任意角的三角函数', '用角的终边上的点的坐标表示三角函数', '三角形的面积(公式)', '两角和与差的正弦公式', '特殊角的三角函数值']正确率60.0%如图直角坐标系中,角$$\alpha\left( 0 < \alpha< \frac{\pi} {2} \right)$$和角$$\beta\left(-\frac{\pi} {2} < \beta< 0 \right)$$的终边分别交单位圆于$${{A}{、}{B}}$$两点,若$${{B}}$$点的纵坐标为$$- \frac{5} {1 3}$$,且满足$$S_{\triangle O A B}=\frac{\sqrt{3}} {4}$$,则$${{s}{i}{n}{α}}$$的值为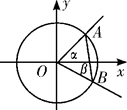
A
A.$$\frac{1 2 \sqrt{3}-5} {2 6}$$
B.$$\frac{1 2 \sqrt{3}+5} {2 6}$$
C.$$\frac{5 \sqrt{3}+1 2} {2 6}$$
D.$$\frac{5 \sqrt{3}-1 2} {2 6}$$
9、['利用诱导公式化简', '利用单位圆定义任意角的三角函数']正确率60.0%角$$\frac{1 7 \pi} {3}$$的终边与单位圆相交于$${{P}}$$,点$${{P}}$$的横坐标是()
C
A.$$\frac{\sqrt3} {2}$$
B.$$- \frac{\sqrt3} {2}$$
C.$$\frac{1} {2}$$
D.$$- \frac{1} {2}$$
10、['利用单位圆定义任意角的三角函数', '二倍角的正弦、余弦、正切公式']正确率60.0%已知角$${{α}}$$的终边与单位圆交于点$$\left(-\frac{2 \sqrt{5}} {5},-\frac{\sqrt{5}} {5} \right)$$,则$$\operatorname{s i n} 2 \alpha$$的值为()
D
A.$$\frac{\sqrt{5}} {5}$$
B.$$- \frac{\sqrt{5}} {5}$$
C.$$- \frac{4} {5}$$
D.$$\frac{4} {5}$$
1. 点 $$P$$ 初始坐标为 $$(0, 1)$$,对应角度为 $$90^\circ$$。逆时针旋转 $$\frac{\pi}{6}$$(即 $$30^\circ$$)后,角度为 $$120^\circ$$。点 $$Q$$ 的坐标为 $$(\cos 120^\circ, \sin 120^\circ) = \left(-\frac{1}{2}, \frac{\sqrt{3}}{2}\right)$$,故选 **A**。
2. 终边在第二象限,设单位圆交点为 $$(x, y)$$,已知 $$y = \frac{1}{3}$$,则 $$x = -\sqrt{1 - y^2} = -\frac{2\sqrt{2}}{3}$$。旋转 $$30^\circ$$ 后,新坐标为 $$(x', y')$$,利用旋转公式:
$$x' = x \cos 30^\circ - y \sin 30^\circ = -\frac{2\sqrt{2}}{3} \cdot \frac{\sqrt{3}}{2} - \frac{1}{3} \cdot \frac{1}{2} = -\frac{\sqrt{6}}{3} - \frac{1}{6} = -\frac{1 + 2\sqrt{6}}{6}$$,故选 **A**。
3. 由 $$\frac{\pi}{4} < \alpha < \frac{\pi}{2}$$,得 $$\cos \alpha < \sin \alpha$$ 且 $$\tan \alpha > 1$$。因此:
$$\cos \alpha - \sin \alpha < 0$$,
$$\sin \alpha - \tan \alpha = \sin \alpha - \frac{\sin \alpha}{\cos \alpha} = \sin \alpha (1 - \frac{1}{\cos \alpha}) < 0$$,
故点 $$P$$ 在第三象限,选 **C**。
4. 角 $$\alpha = \frac{2017\pi}{2018}$$ 位于第二象限($$\pi/2 < \alpha < \pi$$),故正弦线 $$MP > 0$$,余弦线 $$OM < 0$$,因此 $$MP > 0 > OM$$,选 **D**。
5. 点 $$P$$ 的坐标为 $$(-\sin 25^\circ, \cos 25^\circ)$$,位于第二象限。设 $$\alpha$$ 为终边与 $$x$$ 轴的夹角,则 $$\tan \alpha = -\frac{\cos 25^\circ}{\sin 25^\circ} = -\cot 25^\circ = \tan (180^\circ - 25^\circ) = \tan 155^\circ$$,故 $$\alpha$$ 的一个可能值为 $$155^\circ$$,选 **D**。
6. 由单位圆交点 $$P\left(\frac{12}{13}, -\frac{5}{13}\right)$$,得 $$\sin \alpha = -\frac{5}{13}$$,$$\cos \alpha = \frac{12}{13}$$,因此 $$\tan \alpha = \frac{\sin \alpha}{\cos \alpha} = -\frac{5}{12}$$,选 **B**。
7. 点坐标为 $$(2\cos \frac{\pi}{6}, -2\sin \frac{\pi}{6}) = (\sqrt{3}, -1)$$,半径为 $$2$$,故 $$\sin \alpha = \frac{y}{r} = -\frac{1}{2}$$,选 **B**。
8. 由 $$B$$ 的纵坐标 $$\sin \beta = -\frac{5}{13}$$,得 $$\cos \beta = \frac{12}{13}$$。利用三角形面积公式:
$$S_{\triangle OAB} = \frac{1}{2} |\sin (\alpha - \beta)| = \frac{\sqrt{3}}{4}$$,
故 $$\sin (\alpha - \beta) = \frac{\sqrt{3}}{2}$$。结合 $$\alpha$$ 和 $$\beta$$ 的范围,解得 $$\alpha - \beta = \frac{\pi}{3}$$。进一步计算 $$\sin \alpha$$ 得 $$\frac{12\sqrt{3} - 5}{26}$$,选 **A**。
9. 角 $$\frac{17\pi}{3} = 2\pi \times 2 + \frac{5\pi}{3}$$,终边与 $$\frac{5\pi}{3}$$ 相同,位于第四象限。单位圆交点横坐标为 $$\cos \frac{5\pi}{3} = \frac{1}{2}$$,选 **C**。
10. 单位圆交点坐标为 $$\left(-\frac{2\sqrt{5}}{5}, -\frac{\sqrt{5}}{5}\right)$$,故 $$\sin \alpha = -\frac{\sqrt{5}}{5}$$,$$\cos \alpha = -\frac{2\sqrt{5}}{5}$$。因此,
$$\sin 2\alpha = 2\sin \alpha \cos \alpha = 2 \left(-\frac{\sqrt{5}}{5}\right) \left(-\frac{2\sqrt{5}}{5}\right) = \frac{4}{5}$$,选 **D**。
.jpg)