正确率60.0%若$$\operatorname{c o s} x=0,$$则角$${{x}}$$等于()
B
A.$$k \pi, \, k \in{\bf Z}$$
B.$$k \pi+\frac{\pi} {2}, k \in{\bf Z}$$
C.$$2 k \pi+\frac{\pi} {2}, k \in{\bf Z}$$
D.$$2 k \pi-\frac{\pi} {2}, k \in{\bf Z}$$
2、['二倍角的正弦、余弦、正切公式', '特殊角的三角函数值']正确率80.0%$$\operatorname{s i n} \frac\pi{1 2} \operatorname{c o s} \frac\pi{1 2}$$的值为()
A
A.$$\frac{1} {4}$$
B.$$- \frac{1} {4}$$
C.$$\frac{\sqrt{3}} {4}$$
D.$$- \frac{\sqrt{3}} {4}$$
3、['特殊角的三角函数值']正确率60.0%$$\operatorname{c o s} \frac{\pi} {3}=( \eta)$$
B
A.$${{1}}$$
B.$$\frac{1} {2}$$
C.$$\frac{\sqrt2} {2}$$
D.$$\frac{\sqrt3} {2}$$
4、['由图象(表)求三角函数的解析式', '特殊角的三角函数值']正确率40.0%已知函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) \ =\sin\left( \begin{matrix} {\omega x+\varphi} \\ \end{matrix} \right) \ \ \left( \begin{matrix} {\omega> 0} \\ {\left| \varphi\right| < \frac{\pi} {2}} \\ \end{matrix} \right)$$的图象如图所示,则$$\operatorname{t a n} \varphi=$$()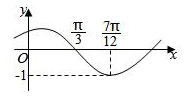
C
A.$$\frac{\sqrt{3}} {3}$$
B.$${{1}}$$
C.$${\sqrt {3}}$$
D.$$- \frac{\sqrt3} {3}$$
5、['利用诱导公式化简', '两角和与差的正弦公式', '特殊角的三角函数值']正确率40.0%$$\operatorname{s i n} 3 6^{\circ} \operatorname{c o s} 6^{\circ}-\operatorname{s i n} 5 4^{\circ} \operatorname{c o s} 8 4^{\circ}$$等于$${{(}{)}}$$
A
A.$$\frac{1} {2}$$
B.$$- \frac{1} {2}$$
C.$$- \frac{\sqrt3} {2}$$
D.$$\frac{\sqrt3} {2}$$
6、['利用诱导公式化简', '利用诱导公式求值', '特殊角的三角函数值']正确率60.0%$$\operatorname{c o s} \frac{2 0 1 8 \pi} {3}=( \textsubscript{\Lambda} )$$
A
A.$$- \frac{1} {2}$$
B.$$\frac{1} {2}$$
C.$$- \frac{\sqrt3} {2}$$
D.$$\frac{\sqrt3} {2}$$
7、['用角的终边上的点的坐标表示三角函数', '特殊角的三角函数值']正确率60.0%已知点$$A ~ ( \textit{x}, \textit{y} )$$是$${{3}{0}^{∘}}$$角终边上异于原点的一点,则$$\frac{y} {x}$$等于()
C
A.$${\sqrt {3}}$$
B.$${{−}{\sqrt {3}}}$$
C.$$\frac{\sqrt{3}} {3}$$
D.$$- \frac{\sqrt3} {3}$$
8、['余弦定理及其应用', '特殊角的三角函数值']正确率60.0%在$${{△}{A}{B}{C}}$$的角$$A, ~ B, ~ C$$所对的边分别为$$a, ~ b, ~ c$$,若$$a^{2}+b^{2}=c^{2}-a b$$,则角$${{C}}$$为()
D
A.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
B.$$\frac{\pi} {3}$$
C.$$\frac{5 \pi} {6}$$
D.$$\frac{2 \pi} {3}$$
9、['函数求值', '特殊角的三角函数值']正确率60.0%已知$$f ( \operatorname{t a n} x )=\operatorname{s i n} 2 x$$,则$$f (-1 )$$的值是()
B
A.$${{1}}$$
B.$${{−}{1}}$$
C.$$\frac{1} {2}$$
D.$${{0}}$$
10、['用角的终边上的点的坐标表示三角函数', '两角和与差的正弦公式', '特殊角的三角函数值']正确率60.0%已知角$${{α}}$$的终边经过$$(-3, 4 )$$,则$$\operatorname{s i n} ( \alpha+\frac{\pi} {4} )$$的值为$${{(}{)}}$$
D
A.$$- \frac{7 \sqrt{2}} {1 0}$$
B.$$\frac{7 \sqrt{2}} {1 0}$$
C.$$- \frac{\sqrt2} {1 0}$$
D.$$\frac{\sqrt2} {1 0}$$
1. 解析:方程 $$\cos x = 0$$ 的解为 $$x = \frac{\pi}{2} + k\pi$$,其中 $$k \in \mathbb{Z}$$。因此正确答案是 B。
2. 解析:利用二倍角公式 $$\sin \theta \cos \theta = \frac{1}{2} \sin 2\theta$$,代入 $$\theta = \frac{\pi}{12}$$,得到 $$\sin \frac{\pi}{12} \cos \frac{\pi}{12} = \frac{1}{2} \sin \frac{\pi}{6} = \frac{1}{4}$$。因此正确答案是 A。
3. 解析:$$\cos \frac{\pi}{3} = \frac{1}{2}$$,因此正确答案是 B。
4. 解析:从图中可以看出,函数在 $$x = 0$$ 处的值为 $$\frac{1}{2}$$,即 $$\sin \varphi = \frac{1}{2}$$。由于 $$|\varphi| < \frac{\pi}{2}$$,可得 $$\varphi = \frac{\pi}{6}$$,因此 $$\tan \varphi = \frac{\sqrt{3}}{3}$$。正确答案是 A。
5. 解析:利用三角恒等式 $$\sin 54^\circ = \cos 36^\circ$$ 和 $$\cos 84^\circ = \sin 6^\circ$$,原式化为 $$\sin 36^\circ \cos 6^\circ - \cos 36^\circ \sin 6^\circ = \sin (36^\circ - 6^\circ) = \sin 30^\circ = \frac{1}{2}$$。因此正确答案是 A。
6. 解析:$$\cos \frac{2018\pi}{3} = \cos \left(672\pi + \frac{2\pi}{3}\right) = \cos \frac{2\pi}{3} = -\frac{1}{2}$$。因此正确答案是 A。
7. 解析:点 $$A(x, y)$$ 在 $$30^\circ$$ 终边上,因此 $$\frac{y}{x} = \tan 30^\circ = \frac{\sqrt{3}}{3}$$。正确答案是 C。
8. 解析:根据余弦定理,$$c^2 = a^2 + b^2 - 2ab \cos C$$。题目给出 $$a^2 + b^2 = c^2 - ab$$,代入得 $$a^2 + b^2 = a^2 + b^2 - 2ab \cos C - ab$$,化简得 $$\cos C = -\frac{1}{2}$$,因此 $$C = \frac{2\pi}{3}$$。正确答案是 D。
9. 解析:设 $$\tan x = -1$$,则 $$x = -\frac{\pi}{4} + k\pi$$。代入 $$f(\tan x) = \sin 2x$$,得 $$f(-1) = \sin \left(-\frac{\pi}{2}\right) = -1$$。因此正确答案是 B。
10. 解析:角 $$\alpha$$ 的终边经过 $$(-3, 4)$$,因此 $$\sin \alpha = \frac{4}{5}$$,$$\cos \alpha = -\frac{3}{5}$$。利用和角公式,$$\sin \left(\alpha + \frac{\pi}{4}\right) = \sin \alpha \cos \frac{\pi}{4} + \cos \alpha \sin \frac{\pi}{4} = \frac{4}{5} \cdot \frac{\sqrt{2}}{2} + \left(-\frac{3}{5}\right) \cdot \frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{10}$$。因此正确答案是 D。
.jpg)