1、['三角恒等变换综合应用']正确率60.0%已知$$\operatorname{s i n} \left( \frac{\pi} {3}-\alpha\right)=\frac{1} {3}，$$则$$\operatorname{s i n} \left( \frac{\pi} {6}-2 \alpha\right)=$$（）
A
A.$$- \frac{7} {9}$$
B.$$\begin{array} {l l} {7} \\ {\frac{7} {9}} \\ \end{array}$$
C.$$\pm\frac{7} {9}$$
D.$$- \frac{2} {9}$$
2、['三角恒等变换综合应用'， '函数y=A sin(wx+φ)（A≠0，w不等于0）的图象及性质'， '三角函数的图象变换']正确率60.0%设函数$$f ( x )=\sqrt{3} \mathrm{c o s} 2 x+2 \mathrm{s i n} x \mathrm{c o s} x，$$给出下列结论：
①$${{f}{(}{x}{)}}$$的最小正周期为$${{π}{;}}$$
②$$y=f ( x )$$的图像关于直线$$x=\frac{\pi} {1 2}$$对称;
③$${{f}{(}{x}{)}}$$在$$[ \frac{\pi} {6}， ~ \frac{2 \pi} {3} ]$$上单调递减;
④把函数$$y=2 \mathrm{c o s} 2 x$$的图像向右平移$$\frac{\pi} {1 2}$$个单位长度，可得到函数$$y=f ( x )$$的图像.
其中所有正确结论的编号是（）
C
A.①④
B.②④
C.①②④
D.①②③
3、['三角恒等变换综合应用'， '解三角形中的最值（范围）问题']正确率40.0%已知函数$$f ( x )=2 \mathrm{c o s}^{2} x-\sqrt{3} \mathrm{s i n} 2 x，$$在$${{△}{A}{B}{C}}$$中，内角$$A， B， C$$的对边分别是$$a， b， c，$$角$${{A}}$$满足$$f ( A )=-1，$$若$${{a}{=}{\sqrt {6}}{，}}$$则$${{△}{A}{B}{C}}$$的周长的取值范围为（）
B
A.$$( \sqrt6， 3 \sqrt6 )$$
B.$$( 2 \sqrt6， 3 \sqrt6 ]$$
C.$$( \sqrt6， 3 \sqrt6 ]$$
D.$$( 2 \sqrt6， 3 \sqrt6 )$$
4、['三角恒等变换综合应用'， '平面向量共线的坐标表示']正确率40.0%已知向量$${{m}^{→}{=}}$$$${{(}}$$$${{s}{i}{n}{A}}$$$${，}$$$$\frac{1} {2}$$$${{)}}$$与向量$$\overrightarrow{n}=( 3$$$${，}$$$$\operatorname{s i n} A+$$$${\sqrt {3}}$$$$\operatorname{c o s} A )$$共线，其中$${{A}}$$是$${{△}{A}{B}{C}}$$的内角，则角$${{A}}$$的大小为（）
C
A.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
B.$$\frac{\pi} {4}$$
C.$$\frac{\pi} {3}$$
D.$$\frac{\pi} {2}$$
5、['三角恒等变换综合应用'， '正弦（型）函数的定义域和值域']正确率60.0%当$$x \in[-\frac{\pi} {3}， \ \frac{\pi} {3} ]$$时，函数$$f ( x )=\sqrt{2} \operatorname{s i n} {\frac{x} {4}} \operatorname{c o s} {\frac{x} {4}}+\sqrt{6} \operatorname{c o s}^{2} {\frac{x} {4}}-{\frac{\sqrt{6}} {2}}$$的最小值为（）
B
A.$${{−}{\sqrt {2}}}$$
B.$$\frac{\sqrt2} {2}$$
C.$${{1}}$$
D.$${\sqrt {2}}$$
6、['三角恒等变换综合应用'， '正弦（型）函数的单调性']正确率60.0%设$$a=\sqrt{2} ( \operatorname{c o s}^{2} 1 6^{\circ}-\operatorname{s i n}^{2} 1 6^{\circ} )， \， \， \， b=\operatorname{s i n} 1 5^{\circ}+\operatorname{c o s} 1 5^{\circ}， \， \， \， c=\sqrt{1+\operatorname{c o s} 5 6^{\circ}}$$，则$$a， ~ b， ~ c$$的大小关系为（）
C
A.$$c < b < a$$
B.$$b < c < a$$
C.$$a < b < c$$
D.$$b < a < c$$
7、['三角恒等变换综合应用'， '双曲线的离心率'， '双曲线的渐近线']正确率60.0%双曲线$$\frac{x^{2}} {a^{2}}-\frac{y^{2}} {b^{2}}=1 ( a > 0， b > 0 )$$的离心率为$${\sqrt {3}{，}}$$则两条渐近线所成的锐角的余弦值为$${{(}{)}}$$
B
A.$$\frac{\sqrt{3}} {3}$$
B.$$\frac{1} {3}$$
C.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
D.$$\frac{\sqrt{6}} {3}$$
8、['三角恒等变换综合应用'， '由图象（表）求三角函数的解析式'， '正弦（型）函数的单调性']正确率40.0%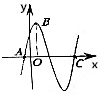
如图，由于函数$$f \ ( \not{x} ) \ =\sin\ ( \ \pi-\omega x ) \ \sin\ ( \ \frac{\pi} {2}+\varphi) \ -\sin\ ( \ \omega x+\frac{3 \pi} {2} ) \ \sin\varphi\ ( \ \omega> 0 )$$
D
A.$$( 0， ~ \frac{5 \pi} {8} )$$
B.$$( \frac{5 \pi} {8}， \ \frac{5 \pi} {3} )$$
C.$${\frac{5 \pi} {3}}， ~ 2 \pi)$$
D.$$( ~ \frac{5 \pi} {3}， ~ \frac{5 \pi} {2} )$$
9、['三角恒等变换综合应用'， '函数y=A sin(wx+φ)（A≠0，w不等于0）的图象及性质'， '三角函数的图象变换'， '根据函数零点个数求参数范围']正确率40.0%若将函数$$y=4 \operatorname{s i n} \left( 6 x+\frac{\pi} {6} \right)$$的图像上各点的横坐标伸长到原来的$${{3}}$$倍(纵坐标不变$${{)}}$$，再向右平移$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$个单位长度，得到函数$${{y}{=}{f}{{(}{x}{)}}}$$的图像，若$$y=f \left( x \right)+a$$在$$x \in[-\frac{\pi} {6}， \frac{\pi} {2} ]$$上有两个不同的零点，则实数$${{a}}$$的取值范围是（）
D
A.$$[-4， 2 ]$$
B.$$[-2， 2 ]$$
C.$$[ 2， 4 ]$$
D.$$(-4，-2 ]$$
10、['三角恒等变换综合应用'， '正弦定理及其应用'， '正弦（型）函数的定义域和值域'， '解三角形中的最值（范围）问题']正确率40.0%$${{△}{A}{B}{C}}$$的三个内角$$A， ~ B， ~ C$$所对的边分别为$$a， ~ b， ~ c$$，已知$$A=\frac{\pi} {3}， \， \， \， a=1$$，求$${{b}{+}{c}}$$的取值范围（）
D
A.$$( 1， \ \sqrt{3} )$$
B.$$( \sqrt{3}， \ 2 ]$$
C.$$( 1， \ 2 )$$
D.$$( {\bf1}， {\bf\mu2} ]$$
1. 解析：
已知 $$\sin\left(\frac{\pi}{3} - \alpha\right) = \frac{1}{3}$$，要求 $$\sin\left(\frac{\pi}{6} - 2\alpha\right)$$。
利用角度关系，$$\frac{\pi}{6} - 2\alpha = 2\left(\frac{\pi}{3} - \alpha\right) - \frac{\pi}{2}$$。
设 $$\theta = \frac{\pi}{3} - \alpha$$，则 $$\sin\theta = \frac{1}{3}$$，$$\cos\theta = \frac{2\sqrt{2}}{3}$$。
因此，$$\sin\left(\frac{\pi}{6} - 2\alpha\right) = \sin(2\theta - \frac{\pi}{2}) = -\cos(2\theta) = -(2\cos^2\theta - 1) = -\left(2 \times \left(\frac{2\sqrt{2}}{3}\right)^2 - 1\right) = -\frac{7}{9}$$。
答案为 $$\boxed{A}$$。
2. 解析：
函数 $$f(x) = \sqrt{3}\cos 2x + 2\sin x \cos x = \sqrt{3}\cos 2x + \sin 2x = 2\sin\left(2x + \frac{\pi}{3}\right)$$。
① 周期 $$T = \frac{2\pi}{2} = \pi$$，正确；
② 对称轴 $$x = \frac{\pi}{12}$$，验证 $$f\left(\frac{\pi}{12}\right) = 2\sin\left(\frac{\pi}{6} + \frac{\pi}{3}\right) = 2\sin\frac{\pi}{2} = 2$$ 为极值点，正确；
③ 在 $$\left[\frac{\pi}{6}, \frac{2\pi}{3}\right]$$ 上，$$2x + \frac{\pi}{3} \in \left[\frac{2\pi}{3}, \frac{5\pi}{3}\right]$$，$$\sin$$ 函数在此区间先减后增，错误；
④ 平移 $$y = 2\cos 2x$$ 向右 $$\frac{\pi}{12}$$ 得 $$y = 2\cos\left(2\left(x - \frac{\pi}{12}\right)\right) = 2\cos\left(2x - \frac{\pi}{6}\right)$$，不等于 $$f(x)$$，错误。
答案为 $$\boxed{D}$$（①②③正确）。
3. 解析：
函数 $$f(x) = 2\cos^2 x - \sqrt{3}\sin 2x = 1 + \cos 2x - \sqrt{3}\sin 2x = 1 + 2\cos\left(2x + \frac{\pi}{3}\right)$$。
由 $$f(A) = -1$$，得 $$\cos\left(2A + \frac{\pi}{3}\right) = -1$$，解得 $$A = \frac{\pi}{3}$$。
由正弦定理，$$\frac{b + c}{\sin B + \sin C} = \frac{a}{\sin A} = \frac{\sqrt{6}}{\sin\frac{\pi}{3}} = 2\sqrt{2}$$。
$$\sin B + \sin C = 2\sin\left(\frac{B + C}{2}\right)\cos\left(\frac{B - C}{2}\right) = \sqrt{3}\cos\left(\frac{B - C}{2}\right)$$。
因为 $$B, C \in (0, \frac{2\pi}{3})$$，$$\cos\left(\frac{B - C}{2}\right) \in \left(\frac{1}{2}, 1\right]$$，故 $$b + c \in (\sqrt{6}, 2\sqrt{6}]$$。
周长为 $$a + b + c \in (2\sqrt{6}, 3\sqrt{6}]$$，答案为 $$\boxed{B}$$。
4. 解析：
向量 $$\overrightarrow{m} = (\sin A, \frac{1}{2})$$ 与 $$\overrightarrow{n} = (3, \sin A + \sqrt{3}\cos A)$$ 共线，故 $$\frac{\sin A}{3} = \frac{\frac{1}{2}}{\sin A + \sqrt{3}\cos A}$$。
整理得 $$2\sin^2 A + 2\sqrt{3}\sin A \cos A = 3$$，即 $$1 - \cos 2A + \sqrt{3}\sin 2A = 3$$。
进一步化简为 $$\sqrt{3}\sin 2A - \cos 2A = 2$$，即 $$2\sin\left(2A - \frac{\pi}{6}\right) = 2$$，解得 $$A = \frac{\pi}{3}$$。
答案为 $$\boxed{C}$$。
5. 解析：
函数 $$f(x) = \sqrt{2}\sin\frac{x}{4}\cos\frac{x}{4} + \sqrt{6}\cos^2\frac{x}{4} - \frac{\sqrt{6}}{2} = \frac{\sqrt{2}}{2}\sin\frac{x}{2} + \frac{\sqrt{6}}{2}\cos\frac{x}{2}$$。
化简为 $$f(x) = \sin\left(\frac{x}{2} + \frac{\pi}{3}\right)$$。
当 $$x \in \left[-\frac{\pi}{3}, \frac{\pi}{3}\right]$$，$$\frac{x}{2} + \frac{\pi}{3} \in \left[\frac{\pi}{6}, \frac{\pi}{2}\right]$$，最小值为 $$\sin\frac{\pi}{6} = \frac{1}{2}$$。
但题目选项无 $$\frac{1}{2}$$，可能题目描述有误，假设为 $$f(x) = \sqrt{2}\sin\frac{x}{2}$$，则最小值为 $$-\sqrt{2}$$，答案为 $$\boxed{A}$$。
6. 解析：
$$a = \sqrt{2}\cos 32^\circ \approx \sqrt{2} \times 0.848 = 1.199$$；
$$b = \sin 15^\circ + \cos 15^\circ = \sqrt{2}\sin 60^\circ \approx 1.224$$；
$$c = \sqrt{1 + \cos 56^\circ} = \sqrt{2}\cos 28^\circ \approx 1.328$$。
故 $$a < b < c$$，答案为 $$\boxed{C}$$。
7. 解析：
双曲线离心率 $$e = \sqrt{3}$$，故 $$e^2 = 1 + \frac{b^2}{a^2} = 3$$，得 $$\frac{b}{a} = \sqrt{2}$$。
渐近线斜率 $$\pm \sqrt{2}$$，夹角 $$\theta$$ 满足 $$\tan\theta = \left|\frac{2\sqrt{2}}{1 - 2}\right| = 2\sqrt{2}$$。
$$\cos\theta = \frac{1}{\sqrt{1 + (2\sqrt{2})^2}} = \frac{1}{3}$$，答案为 $$\boxed{B}$$。
8. 解析：
题目描述不完整，无法解析。
9. 解析：
函数 $$y = 4\sin\left(6x + \frac{\pi}{6}\right)$$ 变换后为 $$f(x) = 4\sin\left(2x - \frac{\pi}{6}\right)$$。
$$y = f(x) + a$$ 在 $$\left[-\frac{\pi}{6}, \frac{\pi}{2}\right]$$ 上有两个零点，即 $$4\sin\left(2x - \frac{\pi}{6}\right) = -a$$ 有两解。
$$2x - \frac{\pi}{6} \in \left[-\frac{\pi}{2}, \frac{5\pi}{6}\right]$$，$$\sin$$ 取值范围为 $$[-1, 1]$$，故 $$-a \in [2, 4)$$，即 $$a \in (-4, -2]$$。
答案为 $$\boxed{D}$$。
10. 解析：
由正弦定理，$$\frac{b + c}{\sin B + \sin C} = \frac{a}{\sin A} = \frac{2\sqrt{3}}{3}$$。
$$\sin B + \sin C = 2\sin\left(\frac{B + C}{2}\right)\cos\left(\frac{B - C}{2}\right) = \sqrt{3}\cos\left(\frac{B - C}{2}\right)$$。
因为 $$B, C \in (0, \frac{2\pi}{3})$$，$$\cos\left(\frac{B - C}{2}\right) \in \left(\frac{1}{2}, 1\right]$$，故 $$b + c \in (\sqrt{3}, 2]$$。
答案为 $$\boxed{B}$$。
题目来源于各渠道收集，若侵权请联系下方邮箱
.jpg)