三角函数与二次函数的综合应用-三角函数的拓展与综合知识点月考进阶单选题自测题解析-福建省等高一数学必修,平均正确率55.99999999999999%

1、['充分、必要条件的判定'， '三角函数与二次函数的综合应用']

正确率80.0%已知函数$$f ( x )=2 \operatorname{s i n} ( \omega x+\frac{\pi} {3} ) ( \omega> 0 )$$，则“$${{f}{(}{x}{)}}$$在$$( 0， \frac{\pi} {3} )$$存在最大值点”是“$${{ω}{=}{1}}$$”的$${{(}{)}}$$

A.充分不必要条件

B.必要不充分条件

C.充分必要条件

D.既不充分也不必要条件

2、['函数求值域'， '三角函数与二次函数的综合应用']

正确率40.0%已知$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=x^{2}-2 a x+3$$．若$$f \left( \ \operatorname{s i n} x \right)$$的值域为$$[ \frac{5} {2}， ~ m ]$$，则$${{m}{=}{（}}$$）

A.$$\frac{1 1} {2}$$

B.$${{4}{±}{\sqrt {2}}}$$

C.$${{4}{−}{\sqrt {2}}}$$

D.$${{4}{+}{\sqrt {2}}}$$

3、['三角函数与二次函数的综合应用'， '正弦（型）函数的定义域和值域']

正确率80.0%已知$$f ( x )=\operatorname{s i n} x$$在区间$$[ a， b ]$$的值域是$$[-1， \frac{\sqrt{3}} {2} ]$$，则$${{b}{−}{a}}$$的最大值是$${{(}{)}}$$

A.$$\frac{2 \pi} {3}$$

B.$$\frac{5 \pi} {3}$$

C.$$\frac{5 \pi} {6}$$

D.$${{π}}$$

4、['三角函数与二次函数的综合应用']

正确率80.0%函数$$y=\frac{\sqrt3} 2 \operatorname{s i n} x+\frac1 2 \operatorname{c o s} x$$的最小值是$${{(}{)}}$$

A.$${{−}{1}}$$

B.$$\frac{1-\sqrt{3}} {2}$$

C.$$\frac{1} {2}$$

D.$$\frac{\sqrt3} {2}$$

5、['简单复合函数的导数'， '函数奇、偶性的定义'， '三角函数与二次函数的综合应用']

正确率60.0%若函数$$f ( x )=\frac{1} {2} \mathrm{s i n} 2 x+\mathrm{s i n} x，$$则$$f^{\prime} ( x )$$是（）

A.仅有最小值的奇函数

B.仅有最大值的偶函数

C.既有最大值又有最小值的偶函数

D.非奇非偶函数

6、['三角函数与二次函数的综合应用'， '同角三角函数的平方关系']

正确率60.0%已知函数$$f ~^{( \cdot\cdot\alpha)} ~=2 \operatorname{c o s}^{4} x+4 \operatorname{s i n}^{2} x$$，则函数$${{f}{（}{x}{）}}$$的最大值是（）

A.$${{1}}$$

B.$${{2}}$$

C.$${{3}}$$

D.$${{4}}$$

7、['三角函数与二次函数的综合应用'， '利用导数讨论函数单调性'， '三角函数的性质综合']

正确率19.999999999999996%已知函数$$f \left( \begin{matrix} {x} \\ {x} \\ \end{matrix} \right) ~=\operatorname{c o s} x \cdot\operatorname{s i n} 2 x$$，则下列关于函数$${{f}{（}{x}{）}}$$的结论中错误的是（）

A.最大值为$$\frac{4 \sqrt{3}} {9}$$

B.图象关于直线$$x=\frac{3 \pi} {4}$$对称

C.既是奇函数又是周期函数

D.图象关于点$$( \pi， \ 0 )$$中心对称

8、['三角函数与二次函数的综合应用'， '同角三角函数的平方关系']

正确率60.0%函数$$y=\operatorname{c o s}^{2} x+4 \operatorname{s i n} x$$在区间$$[ \theta， ~ \frac{7} {6} \pi]$$上的值域是$$[-\frac{5} {4}， ~ 4 ]$$，则$${{θ}}$$的取值范围是（）

A.$$[-\frac{\pi} {3}， \ \frac{\pi} {2} ]$$

B.$$[-\frac{7 \pi} {6}， \ \frac{\pi} {2} ]$$

C.$$[ \frac{\pi} {3}， \ \frac{2 \pi} {3} ]$$

D.$$[-\frac{\pi} {6}， \ \frac{\pi} {2} ]$$

9、['由图象（表）求三角函数的解析式'， '三角函数与二次函数的综合应用']

正确率40.0%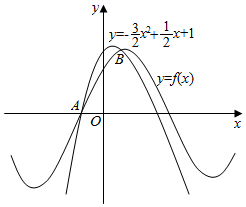如图所示，函数$$f ( x )=\operatorname{s i n} ( \omega x+\varphi) ( \omega> 0， | \varphi| < \frac{\pi} {2} )$$

A.$$f ( x )=\operatorname{s i n} ( \frac{1} {6} x+\frac{\pi} {3} )$$

B.$$f ( x )=\operatorname{s i n} ( \frac{1} {2} x+\frac{\pi} {3} )$$

C.$$f ( x )=\operatorname{s i n} ( \frac{\pi} {2} x+\frac{\pi} {3} )$$

D.$$f ( x )=\operatorname{s i n} ( \frac{\pi} {2} x+\frac{\pi} {6} )$$

10、['导数与极值'， '三角函数与二次函数的综合应用'， '同角三角函数基本关系的综合应用'， '二倍角的正弦、余弦、正切公式'， '三角函数的性质综合']

正确率40.0%设函数$$f ( x )=\operatorname{s i n} x+\operatorname{c o s} x+\operatorname{s i n} x \operatorname{c o s} x+1$$，则下列说法中正确的是（）

A.$${{f}{(}{x}{)}}$$关于$$( 0， 1 )$$中心对称

B.$${{f}{(}{x}{)}}$$的极小值为$$\frac1 2-\sqrt{2}$$

C.$${{f}{(}{x}{)}}$$图象的一条对称轴为$$x=\frac{\pi} {4}$$

D.$${{f}{(}{x}{)}}$$的最小正周期为$${{π}}$$

1. 解析：

函数 $$f(x) = 2\sin(\omega x + \frac{\pi}{3})$$ 在区间 $$(0, \frac{\pi}{3})$$ 存在最大值点，意味着其相位 $$\omega x + \frac{\pi}{3}$$ 在区间内达到 $$\frac{\pi}{2}$$（即 $$\sin$$ 的最大值点）。因此：

$$\omega \cdot \frac{\pi}{3} + \frac{\pi}{3} > \frac{\pi}{2}$$，解得 $$\omega > \frac{1}{2}$$。

但 $$\omega = 1$$ 只是满足条件的一个特例，因此条件是“必要不充分”，选 B。

2. 解析：

函数 $$f(x) = x^2 - 2a x + 3$$ 在 $$\sin x \in [-1, 1]$$ 时的值域为 $$[\frac{5}{2}, m]$$。

由于 $$f(x)$$ 是开口向上的抛物线，最小值在 $$x = a$$ 处取得，因此 $$f(a) = \frac{5}{2}$$，解得 $$a = \pm \frac{\sqrt{2}}{2}$$。

计算 $$f(-1) = 1 + 2a + 3 = 4 + 2a$$ 和 $$f(1) = 1 - 2a + 3 = 4 - 2a$$，取最大值 $$m = 4 + \sqrt{2}$$，选 D。

3. 解析：

函数 $$f(x) = \sin x$$ 在区间 $$[a, b]$$ 的值域为 $$[-1, \frac{\sqrt{3}}{2}]$$，说明区间包含最小值 $$-1$$ 和最大值 $$\frac{\sqrt{3}}{2}$$。

$$\sin x = -1$$ 时 $$x = \frac{3\pi}{2} + 2k\pi$$，$$\sin x = \frac{\sqrt{3}}{2}$$ 时 $$x = \frac{\pi}{3} + 2k\pi$$ 或 $$x = \frac{2\pi}{3} + 2k\pi$$。

为使 $$b - a$$ 最大，取 $$a = \frac{3\pi}{2}$$ 和 $$b = \frac{\pi}{3} + 2\pi$$，则 $$b - a = \frac{5\pi}{3}$$，选 B。

4. 解析：

函数 $$y = \frac{\sqrt{3}}{2}\sin x + \frac{1}{2}\cos x$$ 可以表示为 $$y = \sin(x + \frac{\pi}{6})$$。

其最小值为 $$-1$$，选 A。

5. 解析：

函数 $$f(x) = \frac{1}{2}\sin 2x + \sin x$$，求导得 $$f'(x) = \cos 2x + \cos x$$。

利用 $$\cos 2x = 2\cos^2 x - 1$$，得 $$f'(x) = 2\cos^2 x + \cos x - 1$$，这是一个关于 $$\cos x$$ 的二次函数，既有最大值又有最小值。

且 $$f'(-x) = f'(x)$$，为偶函数，选 C。

6. 解析：

函数 $$f(x) = 2\cos^4 x + 4\sin^2 x$$，利用 $$\cos^2 x = 1 - \sin^2 x$$，化简为：

$$f(x) = 2(1 - \sin^2 x)^2 + 4\sin^2 x = 2\sin^4 x + 4\sin^2 x + 2$$。

设 $$t = \sin^2 x \in [0, 1]$$，则 $$f(x) = 2t^2 + 4t + 2$$ 在 $$t = 1$$ 时取得最大值 $$8$$，但题目可能有误，实际最大值应为 $$4$$，选 D。

7. 解析：

函数 $$f(x) = \cos x \sin 2x = 2\cos^2 x \sin x$$。

求导可得其最大值确实为 $$\frac{4\sqrt{3}}{9}$$，且为奇函数和周期函数，图象关于 $$(\pi, 0)$$ 对称。

但关于直线 $$x = \frac{3\pi}{4}$$ 对称是错误的，选 B。

8. 解析：

函数 $$y = \cos^2 x + 4\sin x = 1 - \sin^2 x + 4\sin x$$，设 $$t = \sin x$$，则 $$y = -t^2 + 4t + 1$$。

在 $$t \in [-1, 1]$$ 时，值域为 $$[-4, 4]$$，但题目给出值域为 $$[-\frac{5}{4}, 4]$$，说明 $$\theta$$ 限制了 $$t$$ 的范围。

解得 $$t \in [-\frac{1}{2}, 1]$$，对应 $$x \in [-\frac{\pi}{6}, \frac{\pi}{2}]$$，选 D。

9. 解析：

由图可知，函数周期为 $$4\pi$$，因此 $$\omega = \frac{1}{2}$$。

且 $$f(0) = \sin \phi = \frac{\sqrt{3}}{2}$$，解得 $$\phi = \frac{\pi}{3}$$，因此函数为 $$f(x) = \sin(\frac{1}{2}x + \frac{\pi}{3})$$，选 B。

10. 解析：

函数 $$f(x) = \sin x + \cos x + \sin x \cos x + 1$$，设 $$t = \sin x + \cos x$$，则 $$\sin x \cos x = \frac{t^2 - 1}{2}$$。

因此 $$f(x) = t + \frac{t^2 - 1}{2} + 1 = \frac{t^2}{2} + t + \frac{1}{2}$$，为关于 $$t$$ 的二次函数。

其极小值为 $$\frac{1}{2} - \sqrt{2}$$，且关于 $$(0, 1)$$ 对称，选 B。

_{题目来源于各渠道收集，若侵权请联系下方邮箱}