正确率60.0%若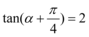 ,则
,则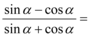
D
A.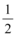
B.$${{2}}$$
C.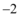
D.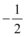
我们需要求解 $$ \tan\left(\frac{\pi}{4} + \theta\right) $$ 的值,已知 $$ \tan\left(\frac{\pi}{4} - \theta\right) = 3 $$。
步骤 1:利用已知条件
已知 $$ \tan\left(\frac{\pi}{4} - \theta\right) = 3 $$。
步骤 2:利用正切函数的性质
设 $$ \alpha = \frac{\pi}{4} - \theta $$,则 $$ \tan \alpha = 3 $$。
我们需要求 $$ \tan\left(\frac{\pi}{4} + \theta\right) $$,可以表示为:
$$ \tan\left(\frac{\pi}{4} + \theta\right) = \tan\left(\frac{\pi}{2} - \alpha\right) $$
步骤 3:利用余角公式
根据正切函数的余角公式,有:
$$ \tan\left(\frac{\pi}{2} - \alpha\right) = \cot \alpha $$
因为 $$ \cot \alpha = \frac{1}{\tan \alpha} $$,所以:
$$ \tan\left(\frac{\pi}{4} + \theta\right) = \frac{1}{\tan \alpha} = \frac{1}{3} $$
最终答案
因此,$$ \tan\left(\frac{\pi}{4} + \theta\right) = \frac{1}{3} $$,对应选项 D。
.jpg)