正确率40.0%函数$$f ( x )=2 \operatorname{s i n} ( \omega x+\varphi)$$,($${{ω}{>}{0}}$$,$$| \varphi| < \frac{\pi} {2}$$)的部分图象如图所示,若对任意$${{x}{∈}{R}}$$,$$f ( x )+f ( 2 t-x )=0$$恒成立,则$${{t}}$$的最小正值为()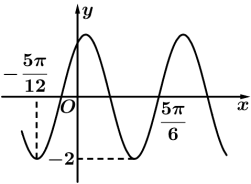
B
A.$$\frac{5 \pi} {1 2}$$
B.$$\frac{\pi} {3}$$
C.$$\frac{\pi} {4}$$
D.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
2、['由图象(表)求三角函数的解析式', '正弦(型)函数的单调性']正确率60.0%函数$$f ( x )=-\sqrt{2} \mathrm{s i n} ( \omega x+\varphi)$$$$( \omega> 0, ~ | \varphi| < ~ \pi)$$的部分图像如图所示,则$${{f}{(}{x}{)}}$$的单调递增区间为()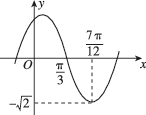
A
A.$$\left[ k \pi-{\frac{5 \pi} {1 2}}, ~ k \pi+{\frac{\pi} {1 2}} \right], ~ k \in{\bf Z}$$
B.$$\left[ k \pi+{\frac{\pi} {1 2}}, ~ k \pi+{\frac{7 \pi} {1 2}} \right], ~ k \in{\bf Z}$$
C.$$\left[ k \pi-\frac{\pi} {2}, ~ k \pi+\frac{\pi} {2} \right], ~ k \in{\bf Z}$$
D.$$\left[ k \pi-{\frac{\pi} {1 2}}, ~ k \pi+{\frac{5 \pi} {1 2}} \right], ~ k \in{\bf Z}$$
3、['由图象(表)求三角函数的解析式', '角α与π±α的三角函数值之间的关系', '正弦(型)函数的单调性']正确率40.0%已知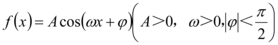 的部分图象如图所示,则$$y=f \left( x+\frac{3 \pi} {8} \right)$$
的部分图象如图所示,则$$y=f \left( x+\frac{3 \pi} {8} \right)$$
C
A.
B.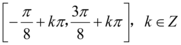
C.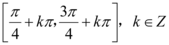
D.
正确率40.0%已知函数$$f ( x )=A \mathrm{s i n} ( \omega x+\varphi) \left( A > 0, \omega> 0, | \varphi| < \frac{\pi} {2} \right)$$的部分图象如图所示,若将$${{f}{{(}{x}{)}}}$$图象上的所有点向右平移$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$个单位得到函数$${{g}{(}{x}{)}}$$的图象,则函数$${{g}{(}{x}{)}}$$的单调递增区间为()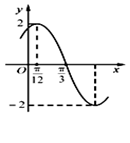
A
A.$$[ k \pi-\frac{\pi} {4}, k \pi+\frac{\pi} {4} ], k \in Z$$
B.$$\left[ 2 k \pi-\frac{\pi} {4}, 2 k \pi+\frac{\pi} {4} \right], k \in Z$$
C.$$\left[ k \pi-\frac{\pi} {3}, k \pi+\frac{\pi} {6} \right], k \in Z$$
D.$$\left[ 2 k \pi-\frac{\pi} {3}, 2 k \pi+\frac{\pi} {6} \right], k \in Z$$
5、['由图象(表)求三角函数的解析式', '正弦(型)函数的零点', '正弦曲线的对称轴']正确率60.0%己知函数$$f ( x )=A \operatorname{s i n} ( \omega x+\varphi) ( A > 0, \omega> 0, | \varphi| < \frac{\pi} {2} )$$在一个周期内的图象如图所示,若方程$$f ( x )=m$$在区间$$[ 0, \pi]$$上有两个不同的实数解$${{x}_{1}{,}{{x}_{2}}}$$,则$${{x}_{1}{+}{{x}_{2}}}$$的值为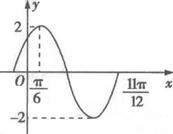
D
A.$$\frac{\pi} {3}$$
B.$$\begin{array} {l l} {2} \\ {\frac{2} {3} \pi} \\ \end{array}$$
C.$$\begin{array} {l l} {\frac{4} {3} \pi} \\ \end{array}$$
D.$$\frac{\pi} {3}$$或$$\begin{array} {l l} {\frac{4} {3} \pi} \\ \end{array}$$
6、['由图象(表)求三角函数的解析式']正确率60.0%弹簧振子的振动是简谐振动.下表给出了振子在完成一次全振动的过程中的事件$${{t}}$$与位移$${{s}}$$之间的测量数据,那么能与这些数据拟合的振动函数的解析式为()
| $${{t}}$$ | $${{0}}$$ | $${{1}}$$ | $${{2}}$$ | $${{3}}$$ | $${{4}}$$ | $${{5}}$$ | $${{6}}$$ | $${{7}}$$ | $${{8}}$$ | $${{9}}$$ | $${{1}{0}}$$ | $${{1}{1}}$$ | $${{1}{2}}$$ |
| $${{s}}$$ | $${{−}{{2}{0}{.}{0}}}$$ | $${{−}{{1}{7}{.}{8}}}$$ | $${{−}{{1}{0}{.}{1}}}$$ | $${{0}{.}{1}}$$ | $${{1}{0}{.}{3}}$$ | $${{1}{.}{7}}$$ | $${{2}{0}{.}{0}}$$ | $${{1}{7}{.}{7}}$$ | $${{1}{0}{.}{3}}$$ | $${{0}{.}{1}}$$ | $${{−}{{1}{0}{.}{1}}}$$ | $${{−}{{1}{7}{.}{8}}}$$ | $${{−}{{2}{0}}}$$ |
D
A.$$s=2 0 \operatorname{s i n} \frac{\pi t} {6}, \ t \in[ 0, \enskip+\infty)$$
B.$$s=2 0 \operatorname{c o s} \frac{\pi t} {6}$$
C.$$s=-2 0 \operatorname{c o s} \frac{\pi t} {6}$$
D.$$s=2 0 \operatorname{s i n} ( \frac{\pi t} {6}-\frac{\pi} {2} ), \, \, \, t \in[ 0, \, \, \, \,+\infty)$$
7、['由图象(表)求三角函数的解析式']正确率60.0%如图,函数$$f ( x )=A \operatorname{s i n} ( 2 x+\varphi) \left( A > 0, | \varphi| < \frac{\pi} {2} \right)$$的图象过点$$( 0, \sqrt{3} )$$,则函数$${{f}{(}{x}{)}}$$的解析式为()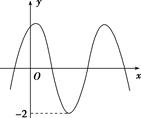
B
A.$$f ( x )=2 \operatorname{s i n} \Bigl( 2 x-\frac{\pi} {3} \Bigr)$$
B.$$f ( x )=2 \operatorname{s i n} \Bigl( 2 x+\frac{\pi} {3} \Bigr)$$
C.$$f ( x )=2 \operatorname{s i n} \left( 2 x+\frac{\pi} {6} \right)$$
D.$$f ( x )=2 \operatorname{s i n} \Bigl( 2 x-\frac{\pi} {6} \Bigr)$$
8、['由图象(表)求三角函数的解析式']正确率60.0%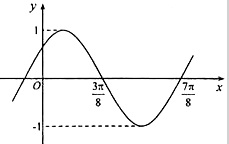 已知函数$$y=\operatorname{s i n} ~ ( \omega x+\varphi) ~ ~ ( \omega> 0, ~ \left| \varphi\right| < \frac{\pi} {2} )$$
已知函数$$y=\operatorname{s i n} ~ ( \omega x+\varphi) ~ ~ ( \omega> 0, ~ \left| \varphi\right| < \frac{\pi} {2} )$$
B
A.$$y=\operatorname{s i n} ~ ( \mathbf{2} x+\frac{\pi} {2} )$$
B.$$y=\operatorname{s i n} ~ ( \2 x+\frac{\pi} {4} )$$
C.$$y=\operatorname{s i n} ~ ( 4 x+\frac{\pi} {2} )$$
D.$$y=\operatorname{s i n} ~ ( 4 x+\frac{\pi} {4} )$$
9、['函数y=A sin(wx+φ)(A≠0,w不等于0)的图象及性质', '由图象(表)求三角函数的解析式']正确率40.0%函数$$f \left( x \right)=A \operatorname{c o s} \left( \omega x+\phi\right)$$的部分图像如图所示,给出以下结论: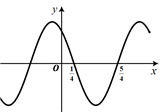
$${①{f}{{(}{x}{)}}}$$
A
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
10、['由图象(表)求三角函数的解析式', '三角函数的图象变换']正确率40.0%函数$$f ( x )=A \operatorname{s i n} ( \omega x+\varphi)+B ( A > 0, \omega> 0, | \varphi| < \frac{\pi} {2} )$$的部分图像如图所示,将函数$${{f}{(}{x}{)}}$$的图像向右平移$${{1}}$$个单位长度得到函数$${{g}{(}{x}{)}}$$的图像,则$$g (-4 )+g ( 1 5 )=~ ( ~ ~ )$$
B
A.$${{3}}$$
B.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
C.$${{2}}$$
D.$$\frac{1} {2}$$
1. 首先,根据图像确定函数的周期和相位。从图中可以看出,函数在 $$x = \frac{\pi}{3}$$ 处取得最大值,且在 $$x = 0$$ 处的值为 $$1$$。因此,可以列出方程:
2. 从图像中可以看出,函数在 $$x = -\frac{\pi}{6}$$ 处取得最小值,且在 $$x = \frac{\pi}{12}$$ 处过零点。因此,可以列出方程:
3. 从图像中可以看出,函数在 $$x = -\frac{\pi}{8}$$ 处取得最大值,且在 $$x = \frac{\pi}{8}$$ 处取得最小值。因此,可以列出方程:
4. 从图像中可以看出,函数在 $$x = \frac{\pi}{12}$$ 处取得最大值,且在 $$x = \frac{7\pi}{12}$$ 处取得最小值。因此,可以列出方程:
5. 从图像中可以看出,函数在 $$x = \frac{\pi}{6}$$ 处取得最大值,且在 $$x = \frac{5\pi}{6}$$ 处取得最小值。因此,可以列出方程:
6. 从表中数据可以看出,振子的周期为 $$12$$ 秒,振幅为 $$20$$。初始时刻 $$t = 0$$ 时,位移为 $$-20$$,说明函数为余弦函数的相反数或正弦函数的相位移动。因此,函数为:
7. 函数图像过点 $$(0, \sqrt{3})$$,因此:
8. 从图像中可以看出,函数在 $$x = -\frac{\pi}{8}$$ 处取得最大值,且在 $$x = \frac{\pi}{8}$$ 处取得最小值。因此,可以列出方程:
9. 从图像中可以看出,函数在 $$x = 0$$ 处取得最大值,且在 $$x = \frac{\pi}{2}$$ 处过零点。因此,可以列出方程:
10. 从图像中可以看出,函数的振幅为 $$1$$,垂直位移为 $$\frac{1}{2}$$,周期为 $$4$$。因此:
.jpg)