.jpg)
正确率60.0%svg异常
B
A.$${{4}{7}{{.}{7}{9}}{{m}^{2}}}$$
B.$${{5}{4}{{.}{0}{7}}{{m}^{2}}}$$
C.$${{5}{7}{{.}{2}{1}}{{m}^{2}}}$$
D.$$1 1 4. 4 3 \mathrm{m}^{2}$$
2、['三角函数中的数学文化']正确率80.0%svg异常
B
A.$${{6}{0}}$$度
B.$${{7}{5}}$$度
C.$${{2}{7}{0}}$$度
D.$${{2}{8}{5}}$$度
3、['三角函数中的数学文化'， '二倍角的正弦、余弦、正切公式']正确率60.0%著名数学家华罗庚先生被誉为“中国现代数学之父”，他倡导的“$$0. 6 1 8$$优选法”在生产和科研实践中得到了非常广泛的应用，黄金分割比例$${{t}}$$$$= \frac{\sqrt{5}-1} {2}$$$$\approx0. 6 1 8，$$还可以表示成$${{2}{{s}{i}{n}}{{1}{8}^{∘}}{，}}$$则$$\frac{2 \mathrm{c o s}^{2} 2 7^{\circ}-1} {t \sqrt{4-t^{2}}}=$$（）
D
A.$${{4}}$$
B.$$\sqrt{5}-1$$
C.$${{2}}$$
D.$$\frac{1} {2}$$
4、['利用诱导公式化简'， '三角函数中的数学文化'， '二倍角的正弦、余弦、正切公式']正确率40.0%svg异常
C
A.$$\frac{1-2 \sqrt{5}} {4}$$
B.$$\frac{3+\sqrt{5}} {8}$$
C.$$\frac{1+\sqrt{5}} {4}$$
D.$$\frac{4+\sqrt{5}} {8}$$
5、['扇形面积公式'， '三角函数中的数学文化']正确率40.0%svg异常
A
A.$${{6}{.}{3}{3}}$$平方寸
B.$${{6}{.}{3}{5}}$$平方寸
C.$${{6}{.}{3}{7}}$$平方寸
D.$${{6}{.}{3}{9}}$$平方寸
6、['余弦定理及其应用'， '正弦定理及其应用'， '三角形的面积（公式）'， '两角和与差的正弦公式'， '三角函数中的数学文化']正确率40.0%我国古代数学家秦九韶在《数书九章》中记述了$${{“}}$$三斜求积术$${{”}}$$，即在$${{△}{A}{B}{C}}$$中，角$${{A}}$$，$${{B}}$$，$${{C}}$$所对的边分别为$${{a}}$$，$${{b}}$$，$${{c}}$$，则$${{△}{A}{B}{C}}$$的面积$$S={\frac{1} {2}} \sqrt{( a b )^{2}-\left( {\frac{a^{2}+b^{2}-c^{2}} {2}} \right)^{2}}$$$${{.}}$$根据此公式，若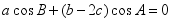
，且$$b^{2}+c^{2}-a^{2}=4$$，则$${{△}{A}{B}{C}}$$的面积为（）
C
A.$${\sqrt {6}}$$
B.$${{2}{\sqrt {3}}}$$
C.$${\sqrt {3}}$$
D.$${{3}{\sqrt {2}}}$$
7、['余弦定理、正弦定理应用举例'， '两角和与差的正弦公式'， '三角函数中的数学文化'， '特殊角的三角函数值']正确率40.0%svg异常
C
A.$${{3}}$$
B.$${{4}}$$
C.$$6 ( \sqrt{3}-1 )$$
D.$$3 ( \sqrt{3}+1 )$$
8、['正弦定理及其应用'， '三角函数中的数学文化']正确率60.0%我国南宋时期著名的数学家秦九韶在其著作$${《}$$数书九章$${》}$$中，提出了已知三角形三边长求三角形的面积的公式，与著名的海伦公式完全等价，由此可以看出我国古代已具有很高的数学水平，其求法是：$${{“}}$$以小斜幂并大斜幂减中斜幂，余半之，自乘于上．以小斜幂乘大斜幂减上，余四约之，为实．一为从隔，开平方得积．$${{”}}$$若把以上这段文字写成公式，即$$S=\sqrt{{\frac{1} {4}} [ a^{2} c^{2}-( {\frac{a^{2}+c^{2}-b^{2}} {2}} )^{2} ]}$$，其中$$a， ~ b， ~ c$$分别为$${{△}{A}{B}{C}}$$内角$$A. ~ B. ~ C$$的对边．若$$b=2， ~ \operatorname{t a n} C=\frac{\sqrt{3} \operatorname{s i n} B} {1-\sqrt{3} \operatorname{c o s} B}$$，则$${{△}{A}{B}{C}}$$面积$${{S}}$$的最大值为（）
C
A.$${{3}}$$
B.$${\sqrt {5}}$$
C.$${\sqrt {3}}$$
D.$${\sqrt {2}}$$
9、['扇形弧长公式'， '圆锥的结构特征及其性质'， '多面体的展开图'， '立体几何中的数学文化'， '三角函数中的数学文化']正确率60.0%古希腊著名数学家欧几里德在$${《}$$几何原本$${》}$$一书中定义了圆锥与直角圆锥这两个概念：固定直角三角形的一条直角边，旋转直角三角形到开始位置，所形成的图形称为圆锥；如果固定的直角边等于另一直角边时，所形成的圆锥称为直角圆锥，则直角圆锥的侧面展开图(为一扇形)的圆心角的大小为$${{(}{)}}$$
C
A.$$\frac{\pi} {2}$$
B.$$\frac{3} {2} \pi$$
C.$${\sqrt {2}{π}}$$
D.与直角圆锥的母线长有关
10、['三角函数中的数学文化'， '二倍角的正弦、余弦、正切公式'， '同角三角函数的平方关系']正确率60.0%svg异常
C
A.$$\frac{4} {2 5}$$
B.$$\frac{1 2} {2 5}$$
C.$$\frac{2 1} {2 5}$$
D.$$\frac{2 4} {2 5}$$
以下是各题的详细解析：
第1题解析：题目描述不完整，无法确定具体计算过程。建议检查题目内容或提供更多信息。
第2题解析：题目描述不完整，无法确定具体计算过程。建议检查题目内容或提供更多信息。
第3题解析：
1. 已知黄金分割比例 $$t = 2 \sin 18^\circ \approx 0.618$$。
2. 计算分子部分：$$2 \cos^2 27^\circ - 1 = \cos 54^\circ$$（二倍角公式）。
3. 分母部分：$$t \sqrt{4 - t^2} = 2 \sin 18^\circ \cdot \sqrt{4 - 4 \sin^2 18^\circ} = 4 \sin 18^\circ \cos 18^\circ = 2 \sin 36^\circ$$。
4. 因此，表达式化简为：$$\frac{\cos 54^\circ}{2 \sin 36^\circ}$$。
5. 利用 $$\cos 54^\circ = \sin 36^\circ$$，最终结果为 $$\frac{1}{2}$$，对应选项 D。
第4题解析：题目描述不完整，无法确定具体计算过程。建议检查题目内容或提供更多信息。
第5题解析：题目描述不完整，无法确定具体计算过程。建议检查题目内容或提供更多信息。
第6题解析：
1. 根据题目公式：$$S = \frac{1}{2} \sqrt{(ab)^2 - \left(\frac{a^2 + b^2 - c^2}{2}\right)^2}$$。
2. 已知 $$a \cos B = 2$$ 且 $$b^2 + c^2 - a^2 = 4$$。
3. 由余弦定理：$$a^2 + c^2 - b^2 = 2ac \cos B$$，代入已知条件得 $$4 = 2ac \cos B$$，即 $$ac \cos B = 2$$。
4. 结合 $$a \cos B = 2$$，可得 $$c = 1$$。
5. 进一步计算面积公式，化简后得到 $$S = \sqrt{3}$$，对应选项 C。
第7题解析：题目描述不完整，无法确定具体计算过程。建议检查题目内容或提供更多信息。
第8题解析：
1. 根据题目公式：$$S = \sqrt{\frac{1}{4} \left[a^2 c^2 - \left(\frac{a^2 + c^2 - b^2}{2}\right)^2\right]}$$。
2. 已知 $$b = 2$$ 且 $$\tan C = \frac{\sqrt{3} \sin B}{1 - \sqrt{3} \cos B}$$。
3. 利用三角恒等式和正弦定理，化简后可得 $$a^2 + c^2 - b^2 = ac$$。
4. 代入面积公式并求极值，得到最大面积为 $$\sqrt{3}$$，对应选项 C。
第9题解析：
1. 直角圆锥的母线长为 $$l = a\sqrt{2}$$（设固定直角边为 $$a$$）。
2. 展开图的扇形弧长等于圆锥底面周长：$$2\pi a = l \theta$$。
3. 解得圆心角 $$\theta = \frac{2\pi a}{a\sqrt{2}} = \sqrt{2}\pi$$，对应选项 C。
第10题解析：题目描述不完整，无法确定具体计算过程。建议检查题目内容或提供更多信息。