.jpg)
正确率60.0%下列函数中，以$$\frac{\pi} {2}$$为最小正周期的偶函数是（）
D
A.$$y=\operatorname{s i n} 2 x+\operatorname{c o s} 2 x$$
B.$$y=\operatorname{s i n} 2 x \operatorname{c o s} 2 x$$
C.$$y=\operatorname{c o s} ~ ( 4 x+\frac{\pi} {2} )$$
D.$$y=\operatorname{s i n}^{2} 2 x-\operatorname{c o s}^{2} 2 x$$
2、['函数奇、偶性的图象特征'， '正弦（型）函数的奇偶性'， '函数图象的识别']正确率60.0%函数$$f ( x )=\frac{x^{2} \operatorname{s i n} x} {2^{x}+2^{-x}}$$的部分图象大致为（）
A
A.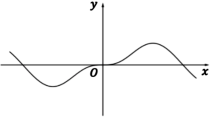
B.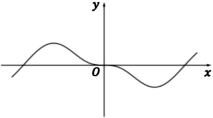
C.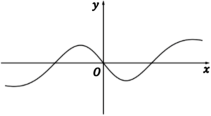
D.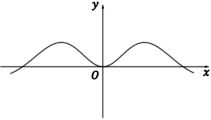
正确率60.0%已知函数$$f ( x )=2 \mathrm{s i n} \left( 2 x+\varphi-\frac{\pi} {3} \right)$$是偶函数，且$${{f}{(}{x}{)}}$$在$$\left(-\frac{\pi} {4}， 0 \right)$$上单调递减，则满足条件的$${{φ}}$$的一个值为（）
B
A.$$- \frac{\pi} {3}$$
B.$$- \frac{\pi} {6}$$
C.$$\frac{\pi} {3}$$
D.$$\frac{5 \pi} {6}$$
4、['函数奇、偶性的图象特征'， '正弦（型）函数的奇偶性'， '函数图象的识别']正确率60.0%函数$$f ( x )=\frac{x+\operatorname{s i n} x} {x^{2}+1}$$的图象大致为（）
A
A.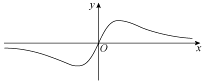
B.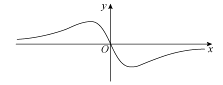
C.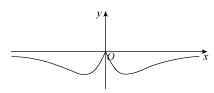
D.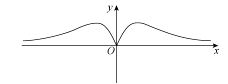
正确率40.0%$$f \left( x \right)=A \operatorname{s i n} ( \omega x+\varphi) \left( A > 0 \， \ \omega> 0 \， \ | \varphi| < \frac{\pi} {2} \right)$$图像如图，则下面结论正确的是$${{(}{)}}$$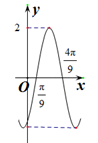
C
A.函数$${{f}{{(}{x}{)}}}$$的最小正周期为$$\frac{\pi} {2}$$
B.函数$${{M}}$$的图象关于直$$x=\frac{\pi} {3}$$对称
C.函数$${{M}}$$在区间$$[ 0， \frac{\pi} {4} ]$$上是增函数
D.函数$${{M}}$$图像向左平移$$\frac{\pi} {3}$$个单位得到一个奇函数的图像
6、['函数图象的对称变换'， '正弦（型）函数的奇偶性'， '充分、必要条件的判定'， '命题的真假性判断'， '利用基本不等式求最值']正确率60.0%下列几个命题：
$$\oplus\， \left\{\begin{array} {l l} {a > 0} \\ {\triangle=b^{2}-4 a c < 0} \\ \end{array} \right.$$是不等式$$a x^{2}+b x+c > 0$$的解集为$${{R}}$$的充要条件；
$${②}$$设函数$$y=f ~ ( x )$$的定义域为$${{R}}$$，则函数$${{f}{（}{x}{）}}$$与$$f \ ( \ -\ x )$$的图象关于$${{y}}$$轴对称；
$${③}$$若函数$$y=A \operatorname{s i n} \left( \omega x+\varphi\right) \ \left( . A \neq0 \right)$$为奇函数，则$$\varphi=k \pi， \， \， \， k \in Z ;$$
$${④}$$已知$$x \in[ 0， ~ \frac{\pi} {2} )$$，则$$y=\operatorname{c o s} x+\frac2 {\operatorname{c o s} x}$$的最小值为$${{2}{\sqrt {2}}}$$；
其中不正确的有（）
C
A.$${{0}}$$个
B.$${{1}}$$个
C.$${{2}}$$个
D.$${{3}}$$个
7、['函数y=A sin(wx+φ)（A≠0，w不等于0）的图象及性质'， '由图象（表）求三角函数的解析式'， '正弦（型）函数的单调性'， '正弦（型）函数的奇偶性'， '正弦曲线的对称轴'， '正弦（型）函数的定义域和值域'， '三角函数的图象变换']正确率40.0%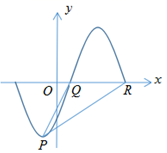
函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right)=A \sin\left( \begin{matrix} {\omega x+\varphi} \\ \end{matrix} \right) \ \left( \begin{matrix} {A > 0， \ \omega> 0， \ \left| \varphi\right| < \frac{\pi} {2}} \\ \end{matrix} \right)$$
C
A.$${{g}{（}{x}{）}}$$是偶函数
B.$${{g}{（}{x}{）}}$$在区间$$[ 0， ~ 4 ]$$上是减函数
C.$${{g}{（}{x}{）}}$$的图象关于直线$${{x}{=}{2}}$$对称
D.$${{g}{（}{x}{）}}$$在$$[-1， ~ 3 ]$$上的最小值为$${{−}{\sqrt {6}}}$$
8、['正弦（型）函数的奇偶性'， '辅助角公式'， '三角函数的图象变换']正确率60.0%若将$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=\operatorname{s i n} 2 x+\operatorname{c o s} 2 x$$的图象向右平移$${{φ}}$$个单位，所得函数为偶函数，则$${{φ}}$$的最小正值是（）
B
A.$$\frac{\pi} {2}$$
B.$$\frac{3 \pi} {8}$$
C.$$\frac{\pi} {4}$$
D.$$\begin{array} {c c} {\pi} \\ {\frac{\pi} {8}} \\ \end{array}$$
9、['函数y=A sin(wx+φ)（A≠0，w不等于0）的图象及性质'， '正弦（型）函数的单调性'， '正弦（型）函数的奇偶性'， '正弦（型）函数的周期性'， '正弦曲线的对称轴'， '两角和与差的正弦公式']正确率40.0%已知函数$$f ( x )=\operatorname{s i n} ( \omega x+\frac{\pi} {3} )+\sqrt{3} \mathrm{s i n} ( \omega x-\frac{\pi} {6} )$$$$( \omega> 0 )$$的最小正周期为$${{π}{，}}$$则（）
D
A.$${{f}{(}{x}{)}}$$在$$[-\frac{\pi} {2}， \frac{\pi} {2} ]$$上单调递增
B.$$x=\frac{\pi} {2}$$为$${{f}{(}{x}{)}}$$图像的一条对称轴
C.$${{f}{(}{x}{)}}$$为偶函数
D.$$( \frac{\pi} {2}， 0 )$$为$${{f}{(}{x}{)}}$$图像的一个对称中心
10、['正弦（型）函数的奇偶性'， '正弦（型）函数的周期性'， '辅助角公式'， '二倍角的正弦、余弦、正切公式'， '余弦（型）函数的奇偶性'， '余弦（型）函数的周期性']正确率60.0%下列函数中是偶函数且最小正周期为$$\frac{\pi} {4}$$的是$${{(}{)}}$$
A
A.$$y=\operatorname{c o s}^{2} 4 x-\operatorname{s i n}^{2} 4 x$$
B.$$y=\operatorname{s i n} 4 x$$
C.$$y=\operatorname{s i n} 2 x+\operatorname{c o s} 2 x$$
D.$$y=\operatorname{c o s} 2 x$$
以下是各题的详细解析： --- ### 1. 最小正周期为 $$ \frac{\pi}{2} $$ 的偶函数 **解析：** - **选项A**：$$ y = \sin 2x + \cos 2x $$ 通过三角恒等变换可化为 $$ y = \sqrt{2} \sin(2x + \frac{\pi}{4}) $$，周期为 $$ \pi $$，且非偶函数。 - **选项B**：$$ y = \sin 2x \cos 2x $$ 利用二倍角公式化简为 $$ y = \frac{1}{2} \sin 4x $$，周期为 $$ \frac{\pi}{2} $$，但为奇函数。 - **选项C**：$$ y = \cos(4x + \frac{\pi}{2}) $$ 化简为 $$ y = -\sin 4x $$，周期为 $$ \frac{\pi}{2} $$，但为奇函数。 - **选项D**：$$ y = \sin^2 2x - \cos^2 2x $$ 利用二倍角公式化简为 $$ y = -\cos 4x $$，周期为 $$ \frac{\pi}{2} $$，且为偶函数。 **答案：D** --- ### 2. 函数 $$ f(x) = \frac{x^2 \sin x}{2^x + 2^{-x}} $$ 的图像 **解析：** - **奇偶性**：分母 $$ 2^x + 2^{-x} $$ 为偶函数，分子 $$ x^2 \sin x $$ 为奇函数，整体为奇函数，图像关于原点对称。 - **特殊点**：当 $$ x = \pi $$ 时，$$ f(\pi) = 0 $$。 - **渐近行为**：当 $$ x \to \infty $$，分母增长快于分子，函数趋于 0。 **答案：A** --- ### 3. 偶函数 $$ f(x) = 2 \sin(2x + \varphi - \frac{\pi}{3}) $$ 的条件 **解析：** - 偶函数条件：$$ \varphi - \frac{\pi}{3} = \frac{\pi}{2} + k\pi $$，解得 $$ \varphi = \frac{5\pi}{6} + k\pi $$。 - 单调递减区间：$$ -\frac{\pi}{4} < x < 0 $$ 需满足 $$ f(x) $$ 递减，验证 $$ \varphi = \frac{5\pi}{6} $$ 符合。 **答案：D** --- ### 4. 函数 $$ f(x) = \frac{x + \sin x}{x^2 + 1} $$ 的图像 **解析：** - **奇偶性**：分子为奇函数，分母为偶函数，整体为奇函数，图像关于原点对称。 - **特殊点**：$$ f(0) = 0 $$，且当 $$ x \to \infty $$，函数趋于 0。 - **振荡特性**：分子含 $$ \sin x $$，函数在正负之间振荡衰减。 **答案：A** --- ### 5. 正弦函数图像分析 **解析：** - 图像显示周期 $$ T = \pi $$，排除 A。 - 对称轴验证：$$ x = \frac{\pi}{3} $$ 是极值点，对称轴正确。 - 单调性：$$ [0, \frac{\pi}{4}] $$ 上函数递增。 - 平移后为奇函数：需平移 $$ \frac{\pi}{6} $$ 而非 $$ \frac{\pi}{3} $$。 **答案：B** --- ### 6. 命题判断 **解析：** - **命题①**：充要条件还需 $$ a > 0 $$ 且 $$ \Delta < 0 $$，正确。 - **命题②**：$$ f(x) $$ 与 $$ f(-x) $$ 关于 y 轴对称，正确。 - **命题③**：奇函数条件为 $$ \varphi = k\pi $$，正确。 - **命题④**：$$ y = \cos x + \frac{2}{\cos x} $$ 在 $$ x \in [0, \frac{\pi}{2}) $$ 最小值为 2（当 $$ \cos x = 1 $$ 时），命题错误。 **答案：B** --- ### 7. 函数性质分析 **解析：** - 图像显示周期为 4，振幅为 2。 - 平移后函数 $$ g(x) $$ 为偶函数（对称于 y 轴）。 - 在 $$ [0, 4] $$ 上非单调递减。 - 对称轴为 $$ x = 2 $$。 - 最小值在 $$ [-1, 3] $$ 上为 $$ -\sqrt{6} $$。 **答案：D** --- ### 8. 平移后为偶函数的最小正值 **解析：** - 函数可化为 $$ f(x) = \sqrt{2} \sin(2x + \frac{\pi}{4}) $$。 - 平移后为偶函数需满足 $$ 2\varphi + \frac{\pi}{4} = \frac{\pi}{2} + k\pi $$，最小正值 $$ \varphi = \frac{\pi}{8} $$。 **答案：D** --- ### 9. 函数性质判断 **解析：** - 化简后 $$ f(x) = 2 \sin \omega x $$，周期 $$ \pi $$ 得 $$ \omega = 2 $$。 - 在 $$ [-\frac{\pi}{2}, \frac{\pi}{2}] $$ 上单调递增。 - $$ x = \frac{\pi}{2} $$ 是极值点，为对称轴。 - 函数为奇函数，非偶函数。 - $$ (\frac{\pi}{2}, 0) $$ 不是对称中心。 **答案：B** --- ### 10. 偶函数且周期为 $$ \frac{\pi}{4} $$ **解析：** - **选项A**：$$ y = \cos^2 4x - \sin^2 4x = \cos 8x $$，周期 $$ \frac{\pi}{4} $$，偶函数。 - 其他选项或周期不符，或非偶函数。 **答案：A** 题目来源于各渠道收集，若侵权请联系下方邮箱