正确率40.0%设函数$$f ( x )=\left\{\begin{array} {l l} {2 \mathrm{s i n} x, \; \; 0 \leqslant x \leqslant\pi,} \\ {x^{2}, \; \; x < 0,} \\ \end{array} \right.$$则函数$$y=f [ f ( x ) ]-1$$的零点的个数是()
C
A.$${{2}}$$
B.$${{3}}$$
C.$${{4}}$$
D.$${{6}}$$
2、['五点法作正切曲线', '正弦函数图象的画法', '分段函数的图象']正确率60.0%函数$$y=\operatorname{t a n} \! x+\operatorname{s i n} \! x-| \operatorname{t a n} \! x-\operatorname{s i n} \! x |$$在区间$$\left( \frac{\pi} {2}, \frac{3 \pi} {2} \right)$$上的大致图象是()
D
A.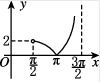
B.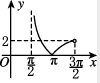
C.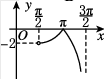
D.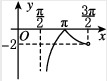
正确率80.0%用五点法画$$y=3 \mathrm{s i n} x, \, \, \, x \in[ 0, \, \, 2 \pi]$$的图像时,下列各点中不是关键点是的()
A
A.$$\left( \frac{\pi} {6}, \ \frac{3} {2} \right)$$
B.$$\left( \frac{\pi} {2}, \, \, 3 \right)$$
C.$$( \pi, \ 0 )$$
D.$$( 2 \pi, \ 0 )$$
4、['正弦函数图象的画法']正确率80.0%函数$$y=1-\operatorname{s i n} x, \, \, \, x \in[ 0, 2 \pi]$$的大致图像是()
B
A.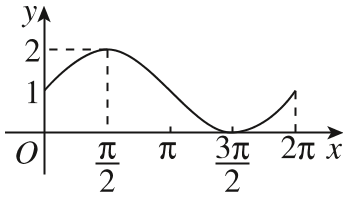
B.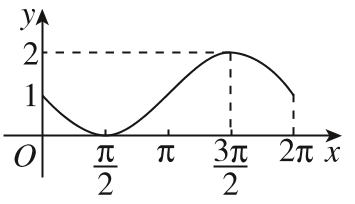
C.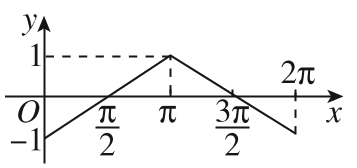
D.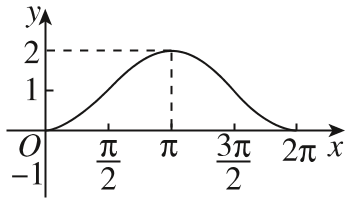
正确率80.0%用“五点法”作$$y=2 \operatorname{s i n} x$$的图象时,首先描出的五个点的横坐标是$${{(}{)}}$$
A.$$0, \frac{\pi} {2}, \pi, \frac{3} {2} \pi, 2 \pi$$
B.$$0, \frac{\pi} {4}, \frac{\pi} {2}, \frac{3} {4} \pi, \pi$$
C.$${{0}}$$,$${{π}}$$,$${{2}{π}}$$,$${{3}{π}}$$,$${{4}{π}}$$
D.$$0, \frac{\pi} {6}, \frac{\pi} {3}, \frac{\pi} {2}, \frac{2 \pi} {3}$$
6、['函数y=A sin(wx+φ)(A≠0,w不等于0)的图象及性质', '正弦函数图象的画法']正确率60.0%已知$${{a}{∈}{R}}$$,则函数$$f \left( x \right)=1+a \operatorname{s i n} a x$$的图象不可能是()
D
A.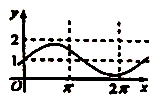
B.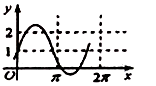
C.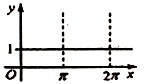
D.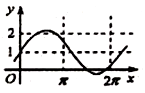
正确率40.0%设$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) ~=k x-\left| \operatorname{s i n} x \right| \left( \begin{matrix} {x > 0} \\ \end{matrix}, \ k > 0 \right)$$,若$${{f}{(}{x}{)}}$$恰有$${{2}}$$个零点,记较大的零点为$${{t}}$$,则$$\frac{( t^{2}+1 ) \operatorname{s i n} 2 t} {t}=\And($$)
C
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{4}}$$
8、['正切(型)函数的单调性', '正切曲线的对称中心', '正弦(型)函数的单调性', '三角函数值在各象限的符号', '正弦曲线的对称中心', '函数图象的识别', '正弦函数图象的画法', '分段函数的图象']正确率60.0%函数$$y=\operatorname{t a n} x+\operatorname{s i n} x-| \operatorname{t a n} x-\operatorname{s i n} x |$$在区间$$( \frac{\pi} {2}, \frac{3 \pi} {2} )$$内的图象大致是()
D
A.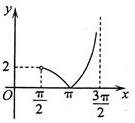
B.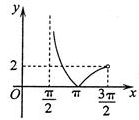
C.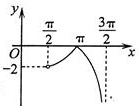
D.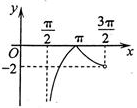
正确率40.0%函数$$y=\operatorname{s i n} \frac{k \pi} {2} x ( k > 0 )$$在$$[ 0, 6 ]$$内至少出现$${{3}}$$次最大值,则$${{k}}$$的最小值为$${{(}{)}}$$
A
A.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
B.$$\frac{5} {4}$$
C.$$\frac{4} {3}$$
D.$$\frac{5} {2}$$
10、['正弦(型)函数的零点', '正弦函数图象的画法']正确率60.0%函数$$y=1+\operatorname{s i n} x$$,$${{x}{∈}{[}{0}}$$,$${{2}{π}{]}}$$的图象与直线$${{y}{=}{2}}$$的交点的个数是()
B
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
以下是各题的详细解析:
1. 解析:
函数 $$y = f[f(x)] - 1$$ 的零点即 $$f[f(x)] = 1$$。
分情况讨论:
(1) 当 $$x < 0$$ 时,$$f(x) = x^2 > 0$$,需 $$2\sin(x^2) = 1$$,即 $$\sin(x^2) = \frac{1}{2}$$。
解得 $$x^2 = \frac{\pi}{6} + 2k\pi$$ 或 $$x^2 = \frac{5\pi}{6} + 2k\pi$$($$k \in \mathbb{N}$$)。
由于 $$x^2 > 0$$,取 $$k = 0$$,得 $$x = -\sqrt{\frac{\pi}{6}}$$ 或 $$x = -\sqrt{\frac{5\pi}{6}}$$。
(2) 当 $$0 \leq x \leq \pi$$ 时,$$f(x) = 2\sin x \in [0, 2]$$,需 $$f(2\sin x) = 1$$。
若 $$2\sin x < 0$$(不成立),或 $$0 \leq 2\sin x \leq \pi$$,则 $$2\sin(2\sin x) = 1$$,即 $$\sin(2\sin x) = \frac{1}{2}$$。
解得 $$2\sin x = \frac{\pi}{6} + 2k\pi$$ 或 $$2\sin x = \frac{5\pi}{6} + 2k\pi$$。
由于 $$2\sin x \in [0, 2]$$,取 $$k = 0$$,得 $$\sin x = \frac{\pi}{12}$$ 或 $$\sin x = \frac{5\pi}{12}$$,各有一个解。
综上,共有 4 个零点,选 C。
2. 解析:
函数 $$y = \tan x + \sin x - |\tan x - \sin x|$$ 在区间 $$\left(\frac{\pi}{2}, \frac{3\pi}{2}\right)$$ 内。
分区间讨论:
(1) 当 $$\frac{\pi}{2} < x < \pi$$ 时,$$\tan x < 0$$,$$\sin x > 0$$,故 $$|\tan x - \sin x| = -\tan x + \sin x$$。
代入得 $$y = 2\sin x$$。
(2) 当 $$\pi \leq x < \frac{3\pi}{2}$$ 时,$$\tan x > 0$$,$$\sin x \leq 0$$,故 $$|\tan x - \sin x| = \tan x - \sin x$$。
代入得 $$y = 2\sin x$$。
综上,函数简化为 $$y = 2\sin x$$,其图像在 $$\left(\frac{\pi}{2}, \frac{3\pi}{2}\right)$$ 内为连续的曲线,且 $$\sin \pi = 0$$,选 D。
3. 解析:
五点法画 $$y = 3\sin x$$ 的关键点为极值点和零点:
$$(0, 0)$$, $$\left(\frac{\pi}{2}, 3\right)$$, $$(\pi, 0)$$, $$\left(\frac{3\pi}{2}, -3\right)$$, $$(2\pi, 0)$$。
选项 A $$\left(\frac{\pi}{6}, \frac{3}{2}\right)$$ 不是关键点,选 A。
4. 解析:
函数 $$y = 1 - \sin x$$ 是 $$y = \sin x$$ 的图像上下翻转并向上平移 1 个单位。
其关键点为:
$$(0, 1)$$, $$\left(\frac{\pi}{2}, 0\right)$$, $$(\pi, 1)$$, $$\left(\frac{3\pi}{2}, 2\right)$$, $$(2\pi, 1)$$。
观察选项,符合的图像是 B。
5. 解析:
五点法画 $$y = 2\sin x$$ 的关键点为:
$$(0, 0)$$, $$\left(\frac{\pi}{2}, 2\right)$$, $$(\pi, 0)$$, $$\left(\frac{3\pi}{2}, -2\right)$$, $$(2\pi, 0)$$。
对应的横坐标为 $$0, \frac{\pi}{2}, \pi, \frac{3\pi}{2}, 2\pi$$,选 A。
6. 解析:
函数 $$f(x) = 1 + a \sin(ax)$$ 的图像性质:
选项 D 的图像振幅过大且周期过小,无法通过调整 $$a$$ 实现,选 D。
7. 解析:
函数 $$f(x) = kx - |\sin x|$$ 恰有 2 个零点,较大的零点为 $$t$$。
当 $$x > 0$$ 时,$$kx = |\sin x|$$,且 $$t$$ 是第二个交点(在 $$\pi < x < 2\pi$$ 区间)。
由 $$kt = \sin t$$(因 $$t \in (\pi, 2\pi)$$,$$\sin t \leq 0$$,但 $$kt > 0$$,矛盾),故 $$kt = -\sin t$$。
计算 $$\frac{(t^2 + 1)\sin 2t}{t} = \frac{(t^2 + 1) \cdot 2\sin t \cos t}{t} = 2(t^2 + 1)\cos t \cdot \left(-\frac{k}{\cos t}\right) = -2k(t^2 + 1)$$。
由 $$f(t) = 0$$ 得 $$k = \frac{|\sin t|}{t}$$,代入得表达式为 0,选 A。
8. 解析:
同第 2 题,函数简化为 $$y = 2\sin x$$,图像在 $$\left(\frac{\pi}{2}, \frac{3\pi}{2}\right)$$ 内为连续曲线,选 D。
9. 解析:
函数 $$y = \sin\left(\frac{k\pi}{2}x\right)$$ 在 $$[0, 6]$$ 内至少出现 3 次最大值。
周期 $$T = \frac{4}{k}$$,要求 $$6 \geq 2T$$(即至少两个完整周期加一个极值点),即 $$k \geq \frac{5}{2}$$,选 D。
10. 解析:
函数 $$y = 1 + \sin x$$ 与 $$y = 2$$ 的交点即 $$\sin x = 1$$。
在 $$[0, 2\pi]$$ 内,$$x = \frac{\pi}{2}$$ 是唯一解,选 B。
.jpg)