正确率40.0%函数$$f ( x )=2 \operatorname{s i n} ( \omega x+\varphi)$$,($${{ω}{>}{0}}$$,$$| \varphi| < \frac{\pi} {2}$$)的部分图象如图所示,若对任意$${{x}{∈}{R}}$$,$$f ( x )+f ( 2 t-x )=0$$恒成立,则$${{t}}$$的最小正值为()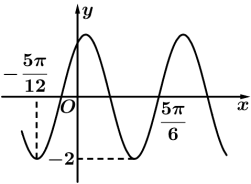
B
A.$$\frac{5 \pi} {1 2}$$
B.$$\frac{\pi} {3}$$
C.$$\frac{\pi} {4}$$
D.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
2、['正弦(型)函数的周期性', '两角和与差的正弦公式', '函数y=Asin(wx+φ) , x∈[0,+∞) (A>0,w>0)中各量的物理意义']正确率60.0%函数$$f ( x )=\frac{\sqrt{3}} {2} \mathrm{s i n} 2 x+\frac{1} {2} \mathrm{c o s} 2 x$$的最小正周期和振幅分别是()
A
A.$${{π}{,}{1}}$$
B.$${{π}{,}{2}}$$
C.$${{2}{π}{,}{1}}$$
D.$${{2}{π}{,}{2}}$$
3、['由图象(表)求三角函数的解析式', '正弦(型)函数的单调性', '正弦(型)函数的周期性']正确率40.0%已知函数$$f ( x )=\sqrt{3} \operatorname{s i n} ( \omega x+\varphi)$$$$\left( \omega> 0, ~-\frac{\pi} {2} < \varphi< \frac{\pi} {2} \right)$$,$$A \left( \frac{1} {3}, \ 0 \right)$$为$${{f}{(}{x}{)}}$$图像的对称中心$${,{B}{,}{C}}$$分别是其图像上相邻的最高点和最低点,若$$| B C |=4,$$则$${{f}{(}{x}{)}}$$的单调递增区间是()
C
A.$$\left( 2 k-\frac{2} {3}, 2 k+\frac{4} {3} \right), k \in{\bf Z}$$
B.$$\left( 2 k \pi-\frac{2} {3} \pi, 2 k \pi+\frac{4} {3} \pi\right), \, \, \, k \in{\bf Z}$$
C.$$\left( 4 k-\frac{2} {3}, 4 k+\frac{4} {3} \right), \, \, \, k \in{\bf Z}$$
D.$$\left( 4 k \pi-\frac{2} {3} \pi, 4 k \pi+\frac{4} {3} \pi\right), \, \, \, k \in{\bf Z}$$
4、['正弦(型)函数的单调性', '正弦曲线的对称中心', '正弦(型)函数的周期性', '正弦曲线的对称轴']正确率60.0%已知点$$P \left(-\frac{\pi} {6}, \ 2 \right)$$是函数$$f ( x )=\operatorname{s i n} ( \omega x+\varphi)+m$$ $$\left( \omega> 0, | \varphi| < \frac{\pi} {2} \right)$$ 的图像的一个对称中心,且点$${{P}}$$到该图像的对称轴的距离的最小值为$$\frac{\pi} {2},$$则()
D
A.$${{f}{(}{x}{)}}$$的最小正周期是$${{π}}$$
B.$${{f}{(}{x}{)}}$$的值域为$$[ 0, ~ 4 ]$$
C.$$\varphi=\frac{\pi} {3}$$
D.$${{f}{(}{x}{)}}$$在区间$$[ \frac{4 \pi} {3}, ~ 2 \pi\brack$$上单调递增
5、['正弦(型)函数的周期性', '三角函数的图象变换']正确率60.0%已知函数$$f ( x )=\operatorname{s i n} ( w x+\varphi) ( w > 0, \ | \varphi| < \frac{\pi} {2} )$$的最小正周期为$${{6}{π}}$$,且取图象向右平移$$\frac{3 \pi} {8}$$个单位后得到函数$$g \ ( \textbf{x} ) \ =\operatorname{s i n} w x$$的图象,则$${{φ}{=}{(}}$$)
A
A.$$\begin{array} {c c} {\pi} \\ {\frac{\pi} {8}} \\ \end{array}$$
B.$$- \frac{\pi} {8}$$
C.$$\frac{\pi} {4}$$
D.$$- \frac{\pi} {4}$$
6、['正弦(型)函数的周期性', '正弦曲线的对称轴', '辅助角公式']正确率40.0%已知函数$$f ( x )=\operatorname{s i n} w x+\sqrt{3} \operatorname{c o s} w x$$的图象与直线$${{y}{=}{2}}$$交于$${{A}{,}{B}}$$两点,若$${{|}{A}{B}{|}}$$的最小值为$${{π}{,}}$$则函数$${{f}{(}{x}{)}}$$的一条对称轴是()
D
A.$$x=\frac{\pi} {3}$$
B.$$x=\frac{\pi} {4}$$
C.$$x=\frac{\pi} {6}$$
D.$$x=\frac{\pi} {1 2}$$
7、['由图象(表)求三角函数的解析式', '正弦(型)函数的单调性', '函数图象的平移变换', '正弦(型)函数的周期性', '辅助角公式', '正弦(型)函数的定义域和值域']正确率40.0%函数$$f \left( x \right)=\sqrt{3} \operatorname{s i n} \omega x+3 \operatorname{c o s} \omega x \left( \omega> 0 \right)$$在一个周期内的图象如图所示,$${{A}}$$为图象的最高点,$${{B}{,}{C}}$$为图象与$${{x}}$$轴的交点,且$${{△}{A}{B}{C}}$$为正三角形,则下列结论中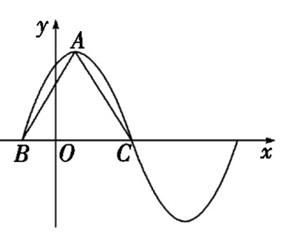
D
A.$${{f}{{(}{x}{)}}}$$的最小正周期为$${{8}}$$
B.$${{f}{{(}{x}{)}}}$$在$$( 3, 4 )$$上单调递减
C.$${{f}{{(}{x}{)}}}$$的值域为$$[-2 \sqrt{3}, 2 \sqrt{3} ]$$
D.$${{f}{{(}{x}{)}}}$$图象上所有的点向右平移$$\frac{4} {3}$$个单位长度后,图象关于$${{y}}$$轴对称
8、['正弦(型)函数的周期性']正确率60.0%函数$$y=\operatorname{s i n} ( 2 x+\frac{\pi} {6} )$$的最小正周期是()
C
A.$${{4}{π}}$$
B.$${{2}{π}}$$
C.$${{π}}$$
D.$$\frac{\pi} {2}$$
9、['正弦(型)函数的单调性', '正弦(型)函数的奇偶性', '探究φ对函数y=Asin(wx+φ)的图象的影响', '正弦(型)函数的周期性', '正弦曲线的对称轴']正确率60.0%将函数$$y=\operatorname{s i n} ( 2 x+\frac{\pi} {3} )$$的图象向右平移$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$个单位长度得到函数$$y=g ( x )$$的图象,则下列选项不成立的是()
D
A.函数$${{g}{(}{x}{)}}$$的最小正周期为$${{π}}$$
B.函数$${{g}{(}{x}{)}}$$的图象关于直线$$x \!=\! \frac{\pi} {4}$$对称
C.函数$${{g}{(}{x}{)}}$$为奇函数
D.函数$${{g}{(}{x}{)}}$$在区间$$[ \frac{\pi} {4}, \pi]$$上单调递减
10、['正弦(型)函数的奇偶性', '正弦曲线的对称中心', '正弦曲线的对称轴', '正弦(型)函数的周期性', '辅助角公式', '两角和与差的正弦公式', '正弦(型)函数的定义域和值域', '导数中不等式恒成立与存在性问题', '函数中的恒成立问题']正确率19.999999999999996%已知函数$$g \left( x \right)=\operatorname{s i n} x+a \operatorname{c o s} x+2 0 1 7$$满足$$g \left( x \right)+g ( \frac{7 \pi} {3}-x )=4 0 3 4$$,又$$f \left( x \right)=a \operatorname{s i n} x+\operatorname{c o s} x$$对任意$${{x}}$$恒有$$f \left( x \right) \leqslant\left| f ( x_{0} ) \right|$$,则满足条件的$${{x}_{0}}$$可以是()
C
A.$$\frac{\pi} {3}$$
B.$$\frac{\pi} {4}$$
C.$$\frac{5 \pi} {6}$$
D.以上选项均不对
1. 解析:根据图像,函数$$f(x)$$的周期$$T=2\pi/\omega$$,由图像可得$$T=4\left(\frac{5\pi}{12}-\frac{\pi}{6}\right)=\pi$$,故$$\omega=2$$。由$$f\left(\frac{\pi}{6}\right)=2$$,代入得$$\varphi=\frac{\pi}{3}$$。由$$f(x)+f(2t-x)=0$$,知$$f(x)$$关于点$$(t,0)$$对称,故$$2t=\frac{\pi}{3}+\frac{5\pi}{6}$$,解得$$t=\frac{7\pi}{12}$$,最小正值为$$\frac{5\pi}{12}$$。答案为A。
3. 解析:由对称中心$$A\left(\frac{1}{3},0\right)$$得$$\frac{\omega}{3}+\varphi=k\pi$$。由$$|BC|=4$$,得$$\sqrt{\left(\frac{T}{2}\right)^2+(2\sqrt{3})^2}=4$$,解得$$T=4$$,$$\omega=\frac{\pi}{2}$$。代入得$$\varphi=-\frac{\pi}{6}$$,故$$f(x)=\sqrt{3}\sin\left(\frac{\pi}{2}x-\frac{\pi}{6}\right)$$,单调递增区间为$$\left(2k-\frac{2}{3},2k+\frac{4}{3}\right)$$。答案为A。
5. 解析:由最小正周期$$6\pi$$得$$\omega=\frac{1}{3}$$。平移后函数为$$g(x)=\sin\left(\frac{1}{3}x-\frac{\pi}{8}+\varphi\right)$$,与$$g(x)=sin\left(\frac{1}{3}x\right)$$对比得$$\varphi=\frac{\pi}{8}$$。答案为B。
7. 解析:函数化简为$$f(x)=2\sqrt{3}\sin\left(\omega x+\frac{\pi}{3}\right)$$。由正三角形性质得周期$$T=8$$,值域$$[-2\sqrt{3},2\sqrt{3}]$$,在$$(3,4)$$上单调递减。平移$$\frac{4}{3}$$后函数为$$2\sqrt{3}\sin\left(\omega x+\frac{\pi}{3}+\frac{\omega}{3}\right)$$,不关于$$y$$轴对称。答案为D。
9. 解析:平移后函数为$$g(x)=\sin\left(2x-\frac{\pi}{3}\right)$$,周期$$\pi$$,关于$$x=\frac{\pi}{4}$$对称,非奇函数,在$$\left[\frac{\pi}{4},\pi\right]$$上单调递减。答案为C。
.jpg)