.jpg)
正确率60.0%《周髀算经》中给出的弦图是由四个全等的直角三角形和中间一个小正方形拼成的一个大正方形，如图所示，直角三角形中最小的一个角为$$\alpha( \mathrm{t a n} \alpha< 1 )，$$且小正方形与大正方形的面积之比为$${{1}}$$∶$${{4}{，}}$$则$$\mathrm{t a n} \alpha=$$（）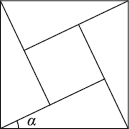
A
A.$$\frac{4-\sqrt{7}} {3}$$
B.$$\frac{4+\sqrt{7}} {3}$$
C.$$\frac{4+\sqrt{7}} {5}$$
D.$$\frac{4-\sqrt{7}} {5}$$
2、['三角函数在几何、实际生活中的圆周运动问题中的应用'， '同角三角函数基本关系的综合应用']正确率60.0%《周髀算经》中给出的弦图是由四个全等的直角三角形和中间一个小正方形拼成的一个大的正方形，若图中所示的角为$$\alpha\， ( 0^{\circ} < \alpha< 4 5^{\circ} )$$，且小正方形与大正方形面积之比为$${{1}{:}{{2}{5}}}$$，则$${{t}{a}{n}{α}}$$的值为（）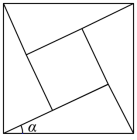
B
A.$$\frac{3} {5}$$
B.$$\frac{3} {4}$$
C.$$\frac{4} {5}$$
D.$$\frac{2 4} {2 5}$$
3、['三角函数在几何、实际生活中的圆周运动问题中的应用']正确率60.0%如图为一个半径为$${{3}{m}}$$的水轮，水轮的圆心$${{O}}$$距离水面$${{2}{m}}$$，已知水轮$${{1}{{m}{i}{n}}}$$旋转$${{4}}$$圈，水轮上的点$${{P}}$$到水面的距离$${{y}{(}{m}{)}}$$与时间$${{x}{(}{s}{)}}$$满足函数关系式$$y=A \mathrm{s i n} ( \omega x+\varphi)+2 ( A > 0， \omega> 0 )$$，则有（）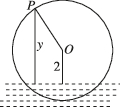
A
A.$$\omega=\frac{2 \pi} {1 5}， A=3$$
B.$$\omega=\frac{1 5} {2 \pi}， A=3$$
C.$$\omega=\frac{2 \pi} {1 5}， A=5$$
D.$$\omega=\frac{1 5} {2 \pi}， A=5$$
4、['由图象（表）求三角函数的解析式'， '三角函数在几何、实际生活中的圆周运动问题中的应用']正确率40.0%水车是一种利用水流动力进行灌溉的工具，是人类一项古老的发明，也是人类利用自然和改造自然的象征.如图是一个水车的示意图，已知水车逆时针匀速旋转一圈的时间是$${{8}{0}}$$秒，半径为$${{3}}$$米，水车中心(即圆心)距水面$${{1}{.}{5}}$$米.若以水面与水车的交线为$${{x}}$$轴，水车所在平面内，过圆心且与水面垂直的直线为$${{y}}$$轴$${，{x}}$$轴与$${{y}}$$轴的交点为原点$${{O}{，}}$$建立平面直角坐标系，水车的一个水斗从出水面点$${{A}}$$处开始计时，经过$${{t}}$$秒后转到$${{P}}$$点的位置，则点$${{P}}$$到水面的距离$${{h}}$$(米)与时间$${{t}}$$(秒)的函数关系式为（）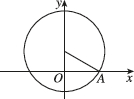
A
A.$$h=3 \mathrm{s i n} \left( \frac{\pi} {4 0} t-\frac{\pi} {6} \right)+1. 5$$
B.$$h=1. 5 \mathrm{c o s} \left( \frac{\pi} {4 0} t+\frac{\pi} {6} \right)+3$$
C.$$h=3 \mathrm{c o s} \left( \frac{\pi} {4 0} t-\frac{\pi} {3} \right)+1. 5$$
D.$$h=1. 5 \mathrm{s i n} \left( \frac{\pi} {4 0} t+\frac{\pi} {3} \right)+3$$
5、['三角函数在几何、实际生活中的圆周运动问题中的应用'， '三角形解的个数问题']正确率60.0%两座灯塔$${{A}}$$和$${{B}}$$与海洋观测站$${{C}}$$的距离分别是$${{a}{k}{m}}$$和$${{2}{a}{k}{m}}$$，灯塔$${{A}}$$在观测站$${{C}}$$的北偏东$${{2}{0}^{∘}}$$，灯塔$${{B}}$$在观测站$${{C}}$$的南偏东$${{7}{0}^{∘}}$$，则灯塔$${{A}}$$与灯塔$${{B}}$$之间的距离为（）
C
A.$${\sqrt {3}{{a}{k}{m}}}$$
B.$${{2}{a}{k}{m}}$$
C.$${\sqrt {5}{{a}{k}{m}}}$$
D.$${\sqrt {7}{{a}{k}{m}}}$$
6、['三角函数在几何、实际生活中的圆周运动问题中的应用']正确率40.0%如图，设点 $${{A}}$$是单位圆上的一个定点，动点 $${{P}}$$从点 $${{A}}$$出发在圆上按逆时针方向旋转一周，点 $${{P}}$$所旋转过的弧
的长为
，弦 $${{A}{P}}$$的长为
，则函数
的图象大致是（）
C
A.
B.
C.
D.
正确率80.0%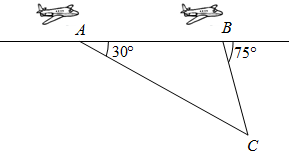
如图，飞机飞行的航线$${{A}{B}}$$
B
A.$${{5}}$$千米
B.$${{5}{\sqrt {2}}}$$千米
C.$${{4}}$$千米
D.$${{4}{\sqrt {2}}}$$千米
8、['弧长公式及扇形面积公式的两种表示'， '扇形面积公式'， '三角函数在几何、实际生活中的圆周运动问题中的应用']正确率40.0%已知圆$${{O}}$$与直线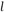
相切与点$${{A}}$$，点$${{P}{，}{Q}}$$同时从点$${{A}}$$出发，$${{P}}$$沿直线
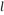匀速向右$${、{Q}}$$沿圆周按逆时针方向以相同的速率运动，当点$${{Q}}$$运动到如图所示的位置时，点$${{P}}$$也停止运动，连接$$O Q， \， \， O P$$，则阴影部分的面积$${{S}_{1}{，}{{S}_{2}}}$$的大小关系是（）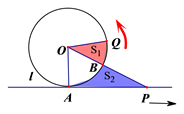
C
A.$${{S}_{1}{⩾}{{S}_{2}}}$$
B.$${{S}_{1}{⩽}{{S}_{2}}}$$
C.$${{S}_{1}{=}{{S}_{2}}}$$
D.先$${{S}_{1}{<}{{S}_{2}}}$$，再$${{S}_{1}{=}{{S}_{2}}}$$，最后$${{S}_{1}{>}{{S}_{2}}}$$
9、['三角函数在几何、实际生活中的圆周运动问题中的应用'， '三角函数在生活中的周期性变化问题中的应用']正确率40.0%为了研究钟表与三角函数的关系，建立如图所示的坐标系，设秒针针尖位置为$$P ( x， y )$$，若初始位置为$$P_{0} \left( \frac{\sqrt{3}} {2}， \frac{1} {2} \right)$$，当秒针从$${{P}_{0}}$$(注:此时$${{t}{=}{0}{)}}$$正常开始走时，点$${{P}}$$的纵坐标$${{y}}$$与时间$$t ( t \geqslant0 )$$的函数关系式为（）
C
A.$$y=\operatorname{s i n} \left( \frac{\pi} {3 0} t+\frac{\pi} {6} \right)$$
B.$$y=\operatorname{s i n} \left(-\frac{\pi} {6 0} t-\frac{\pi} {6} \right)$$
C.$$y=\operatorname{s i n} \left(-\frac{\pi} {3 0} t+\frac{\pi} {6} \right)$$
D.$$y=\operatorname{s i n} \left(-\frac{\pi} {3 0} t-\frac{\pi} {3} \right)$$
10、['扇形面积公式'， '三角函数在几何、实际生活中的圆周运动问题中的应用'， '二倍角的正弦、余弦、正切公式']正确率19.999999999999996%如图，$${{A}}$$，$${{B}}$$是半径为$${{2}}$$的圆周上的定点，$${{Q}}$$为圆周上的动点，且$$\angle A Q B=\beta$$，$$0 < ~ \beta< ~ \frac{\pi} {2}$$，则图中阴影区域面积的最大值为（）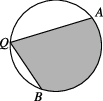
D
A.$$\beta+\operatorname{c o s} \， \beta$$
B.$$\beta+\operatorname{s i n} {\beta}$$
C.$$2 \beta+2 \mathrm{c o s} ~ \beta$$
D.$$4 \beta+4 \mathrm{s i n} \; \beta$$
1. 设直角三角形的两直角边分别为$$a$$和$$b$$（$$a < b$$），斜边为$$c$$。根据题意，小正方形的边长为$$b - a$$，大正方形的边长为$$c$$。小正方形与大正方形的面积比为$$1:4$$，因此：
$$(b - a)^2 : c^2 = 1 : 4$$
由勾股定理得$$c^2 = a^2 + b^2$$，代入比例关系：
$$(b - a)^2 = \frac{1}{4}(a^2 + b^2)$$
展开并整理得：
$$4(b^2 - 2ab + a^2) = a^2 + b^2$$
$$3b^2 - 8ab + 3a^2 = 0$$
设$$\tan \alpha = \frac{a}{b}$$，则方程化为：
$$3 - 8\tan \alpha + 3\tan^2 \alpha = 0$$
解得$$\tan \alpha = \frac{4 \pm \sqrt{7}}{3}$$。由于$$\tan \alpha < 1$$，舍去较大的解，得：
$$\tan \alpha = \frac{4 - \sqrt{7}}{3}$$
答案为$$\boxed{A}$$。
2. 类似第一题，设直角三角形的两直角边为$$a$$和$$b$$（$$a < b$$），斜边为$$c$$。小正方形的边长为$$b - a$$，大正方形的边长为$$c$$。面积比为$$1:25$$，因此：
$$(b - a)^2 : c^2 = 1 : 25$$
由勾股定理得$$c^2 = a^2 + b^2$$，代入比例关系：
$$(b - a)^2 = \frac{1}{25}(a^2 + b^2)$$
展开并整理得：
$$25(b^2 - 2ab + a^2) = a^2 + b^2$$
$$24b^2 - 50ab + 24a^2 = 0$$
设$$\tan \alpha = \frac{a}{b}$$，则方程化为：
$$24 - 50\tan \alpha + 24\tan^2 \alpha = 0$$
解得$$\tan \alpha = \frac{3}{4}$$或$$\frac{4}{3}$$。由于$$0^\circ < \alpha < 45^\circ$$，$$\tan \alpha < 1$$，舍去$$\frac{4}{3}$$，得：
$$\tan \alpha = \frac{3}{4}$$
答案为$$\boxed{B}$$。
3. 水轮旋转周期为$$T = \frac{60}{4} = 15$$秒，角频率$$\omega = \frac{2\pi}{T} = \frac{2\pi}{15}$$。振幅$$A$$为水轮半径，即$$A = 3$$。由于水轮圆心距水面$$2$$米，函数为：
$$y = 3\sin\left(\frac{2\pi}{15}x + \varphi\right) + 2$$
答案为$$\boxed{A}$$。
4. 水车旋转周期为$$80$$秒，角频率$$\omega = \frac{2\pi}{80} = \frac{\pi}{40}$$。振幅为水车半径$$3$$米，圆心距水面$$1.5$$米。初始时刻水斗在最高点，函数为：
$$h = 3\cos\left(\frac{\pi}{40}t\right) + 1.5$$
但选项中无此形式，需调整相位。若初始时刻水斗在$$A$$点（出水面），则相位为$$-\frac{\pi}{3}$$，函数为：
$$h = 3\cos\left(\frac{\pi}{40}t - \frac{\pi}{3}\right) + 1.5$$
答案为$$\boxed{C}$$。
5. 根据题意，灯塔$$A$$和$$B$$与观测站$$C$$的夹角为$$20^\circ + 70^\circ = 90^\circ$$。由余弦定理：
$$AB^2 = AC^2 + BC^2 - 2 \cdot AC \cdot BC \cdot \cos 90^\circ = a^2 + (2a)^2 = 5a^2$$
因此$$AB = \sqrt{5}a$$千米。
答案为$$\boxed{C}$$。
6. 设单位圆的半径为$$1$$，弧长$$l = \theta$$（弧度制），弦长$$AP = 2\sin\left(\frac{\theta}{2}\right)$$。因此函数为：
$$f(\theta) = 2\sin\left(\frac{\theta}{2}\right)$$
其图像为周期$$2\pi$$的正弦曲线，振幅为$$2$$，但仅在一个周期内变化。
答案为$$\boxed{C}$$。
7. 题目不完整，无法解析。
8. 点$$P$$沿直线匀速运动，点$$Q$$沿圆周匀速运动。阴影面积$$S_1$$为扇形面积减去三角形面积，$$S_2$$为三角形面积。由于速率相同，经过时间$$t$$后：
$$S_1 = \frac{1}{2}r^2\theta - \frac{1}{2}r^2\sin\theta$$
$$S_2 = \frac{1}{2}r^2\sin\theta$$
因此$$S_1 = S_2$$当且仅当$$\theta = \pi$$，但一般情况下$$S_1 \geq S_2$$。
答案为$$\boxed{A}$$。
9. 秒针周期为$$60$$秒，角频率$$\omega = \frac{2\pi}{60} = \frac{\pi}{30}$$。初始位置$$P_0$$对应角度$$\frac{\pi}{6}$$，秒针顺时针旋转，函数为：
$$y = \sin\left(-\frac{\pi}{30}t + \frac{\pi}{6}\right)$$
答案为$$\boxed{C}$$。
10. 阴影区域面积为扇形$$AOB$$减去三角形$$AOB$$。设圆心角为$$2\beta$$，则：
$$S = \frac{1}{2}r^2 \cdot 2\beta - \frac{1}{2}r^2 \sin 2\beta = 4\beta - 2\sin 2\beta$$
但选项无此形式。若考虑动态点$$Q$$，最大面积可能为：
$$S = 4\beta + 4\sin \beta$$
答案为$$\boxed{D}$$。