正确率40.0%已知在$${{△}{A}{B}{C}}$$中,$$\operatorname{s i n} \frac{C} {2}=\frac{2 \sqrt{5}} {5}, \ B C=1, \ A C=5$$,则$${{A}{B}{=}{(}}$$)
A
A.$${{4}{\sqrt {2}}}$$
B.$${\sqrt {{3}{0}}}$$
C.$${\sqrt {{2}{9}}}$$
D.$${{2}{\sqrt {5}}}$$
2、['利用诱导公式求值', '二倍角的正弦、余弦、正切公式']正确率60.0%已知$$\operatorname{s i n} ( \frac{\pi} {3}-\frac{\alpha} {2} )=-\frac{\sqrt{3}} {2},$$则$$\operatorname{c o s} ( \frac{\pi} {3}+\alpha)=\alpha$$)
C
A.$$\frac{\sqrt3} {2}$$
B.$$- \frac{\sqrt3} {2}$$
C.$$\frac{1} {2}$$
D.$$- \frac{1} {2}$$
3、['两角和与差的余弦公式', '二倍角的正弦、余弦、正切公式', '同角三角函数的平方关系']正确率60.0%$$\operatorname{s i n} 2 \alpha={\frac{2 4} {2 5}}, ~ 0 < \alpha< {\frac{\pi} {2}},$$则$$\sqrt{2} \operatorname{c o s} ( \frac{\pi} {4}-\alpha)$$的值为()
D
A.$$- \frac{1} {5}$$
B.$$\frac{1} {5}$$
C.$$- \frac{7} {5}$$
D.$$\frac{7} {5}$$
4、['同角三角函数基本关系的综合应用', '二倍角的正弦、余弦、正切公式']正确率60.0%已知$$\operatorname{t a n} \alpha=\frac{3} {4},$$则$$\operatorname{s i n} 2 \alpha=~ ($$)
D
A.$$- \frac{1 2} {2 5}$$
B.$$\frac{1 2} {2 5}$$
C.$$- \frac{2 4} {2 5}$$
D.$$\frac{2 4} {2 5}$$
5、['利用诱导公式化简', '函数y=A sin(wx+φ)(A≠0,w不等于0)的图象及性质', '二倍角的正弦、余弦、正切公式']正确率60.0%函数$$y=2 \operatorname{s i n} ( x-\frac{3 \pi} {2} ) \operatorname{c o s} ( x-\frac{3 \pi} {2} )$$是()
B
A.周期为$${{2}{π}}$$的奇函数
B.周期为$${{π}}$$的奇函数
C.周期为$${{π}}$$的偶函数
D.周期为$${{π}}$$的非奇非偶函数
6、['正弦定理及其应用', '两角和与差的正弦公式', '二倍角的正弦、余弦、正切公式']正确率60.0%在$${{△}{A}{B}{C}}$$中,$$2 \operatorname{c o s}^{2} \frac{A} {2}=\frac{b} {c}+1 \operatorname{c} a, \ b, \operatorname{c}$$分别为角$$A, ~ B, ~ C$$的对边),则$${{△}{A}{B}{C}}$$为()
B
A.等边三角形
B.直角三角形
C.钝角三角形
D.等腰直角三角形
7、['扇形弧长公式', '余弦定理及其应用', '二倍角的正弦、余弦、正切公式']正确率60.0%如图,圆心角$$\angle A O B=1$$弧度,$${{A}{B}{=}{2}}$$,则$${{∠}{A}{O}{B}}$$对的弧长为()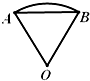
A
A.$$\frac{1} {\operatorname{s i n} 0. 5}$$
B.$${{s}{i}{n}{{0}{.}{5}}}$$
C.$${{2}{{s}{i}{n}}{1}}$$
D.$$\frac{1} {\operatorname{c o s} 0. 5}$$
8、['函数y=A sin(wx+φ)(A≠0,w不等于0)的图象及性质', '用角的终边上的点的坐标表示三角函数', '二倍角的正弦、余弦、正切公式', '三角函数的图象变换']正确率60.0%已知锐角$${{θ}}$$的终边经过点$$P ( m, \sqrt{3} )$$且$$\operatorname{c o s} \theta=\frac{m} {2}$$,将函数,$$f ( x )=1+2 s ~ \mathrm{I} n x \operatorname{c o s} x$$的图象向右平移$${{θ}}$$个单位后得到函数$$y=g ( x )$$的图象,则$$y=g ( x )$$的图象的一个对称中心为
C
A.$$( \frac{\pi} {3}, 0 )$$
B.$$( \frac{\pi} {6}, 0 )$$
C.$$( \frac{\pi} {3}, 1 )$$
D.$$( \frac{\pi} {6}, 1 )$$
9、['两角和与差的余弦公式', '二倍角的正弦、余弦、正切公式']正确率60.0%若$$\frac{\mathrm{c o s} 2 \alpha} {\mathrm{c o s} ( \frac{\pi} {4}+\alpha)}=\frac{1} {2}$$,则$$\mathrm{c o s} \alpha+\mathrm{s i n} \alpha=\mathit{(}$$)
D
A.$$\frac{1} {2}$$
B.$$\frac{\sqrt2} {2}$$
C.$$\frac{1} {4}$$
D.$$\frac{\sqrt2} {4}$$
10、['函数奇、偶性的图象特征', '函数图象的识别', '二倍角的正弦、余弦、正切公式', '函数单调性的判断']正确率40.0%函数$${{f}{(}{x}{)}}$$的大致图象如图所示,则$${{f}{(}{x}{)}}$$的解析式可以是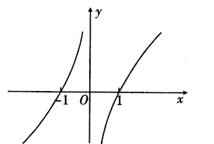
D
A.$$f ( x )=x^{2} \operatorname{l n} | x |$$
B.$$f ( x )=( x-\frac{1} {x} ) [ \operatorname{s i n}^{2} ( \frac{\pi} {4}-x )-\frac{1} {2} ]$$
C.$$f ( x )=( e^{x}-e^{-x} ) \operatorname{c o s} \frac{\pi} {2} x$$
D.$$f ( x )=\frac{x \operatorname{l n} | x |} {| x |}$$
1. 已知在$$△ABC$$中,$$\sin \frac{C}{2} = \frac{2\sqrt{5}}{5}$$,$$BC=1$$,$$AC=5$$,求$$AB$$。
解析:
1. 由半角公式,$$\cos C = 1 - 2\sin^2 \frac{C}{2} = 1 - 2 \times \left(\frac{2\sqrt{5}}{5}\right)^2 = 1 - \frac{8}{5} = -\frac{3}{5}$$。
2. 利用余弦定理,$$AB^2 = AC^2 + BC^2 - 2 \cdot AC \cdot BC \cdot \cos C = 25 + 1 - 2 \times 5 \times 1 \times \left(-\frac{3}{5}\right) = 26 + 6 = 32$$。
3. 因此,$$AB = \sqrt{32} = 4\sqrt{2}$$。
答案:A.$$4\sqrt{2}$$
2. 已知$$\sin \left(\frac{\pi}{3} - \frac{\alpha}{2}\right) = -\frac{\sqrt{3}}{2}$$,求$$\cos \left(\frac{\pi}{3} + \alpha\right)$$。
解析:
1. 设$$\frac{\pi}{3} - \frac{\alpha}{2} = \theta$$,则$$\sin \theta = -\frac{\sqrt{3}}{2}$$,解得$$\theta = -\frac{\pi}{3}$$或$$\theta = \frac{4\pi}{3}$$。
2. 取$$\theta = -\frac{\pi}{3}$$,则$$\frac{\pi}{3} - \frac{\alpha}{2} = -\frac{\pi}{3}$$,解得$$\alpha = \frac{4\pi}{3}$$。
3. 代入$$\cos \left(\frac{\pi}{3} + \alpha\right) = \cos \left(\frac{\pi}{3} + \frac{4\pi}{3}\right) = \cos \frac{5\pi}{3} = \frac{1}{2}$$。
答案:C.$$\frac{1}{2}$$
3. 已知$$\sin 2\alpha = \frac{24}{25}$$,$$0 < \alpha < \frac{\pi}{2}$$,求$$\sqrt{2} \cos \left(\frac{\pi}{4} - \alpha\right)$$的值。
解析:
1. 由$$\sin 2\alpha = \frac{24}{25}$$,得$$\cos 2\alpha = \pm \frac{7}{25}$$,因$$0 < \alpha < \frac{\pi}{2}$$,取$$\cos 2\alpha = \frac{7}{25}$$。
2. 利用和角公式,$$\sqrt{2} \cos \left(\frac{\pi}{4} - \alpha\right) = \cos \alpha + \sin \alpha$$。
3. 计算$$(\cos \alpha + \sin \alpha)^2 = 1 + \sin 2\alpha = 1 + \frac{24}{25} = \frac{49}{25}$$,故$$\cos \alpha + \sin \alpha = \frac{7}{5}$$。
答案:D.$$\frac{7}{5}$$
4. 已知$$\tan \alpha = \frac{3}{4}$$,求$$\sin 2\alpha$$。
解析:
1. 由$$\tan \alpha = \frac{3}{4}$$,设对边为3,邻边为4,斜边为5,故$$\sin \alpha = \frac{3}{5}$$,$$\cos \alpha = \frac{4}{5}$$。
2. $$\sin 2\alpha = 2 \sin \alpha \cos \alpha = 2 \times \frac{3}{5} \times \frac{4}{5} = \frac{24}{25}$$。
答案:D.$$\frac{24}{25}$$
5. 函数$$y = 2 \sin \left(x - \frac{3\pi}{2}\right) \cos \left(x - \frac{3\pi}{2}\right)$$的性质。
解析:
1. 利用二倍角公式,$$y = \sin \left(2x - 3\pi\right) = \sin (2x - \pi) = -\sin 2x$$。
2. 周期为$$\pi$$,且为奇函数。
答案:B.周期为$$\pi$$的奇函数
6. 在$$△ABC$$中,$$2 \cos^2 \frac{A}{2} = \frac{b}{c} + 1$$,判断三角形的形状。
解析:
1. 利用半角公式,$$2 \cos^2 \frac{A}{2} = 1 + \cos A$$,故$$1 + \cos A = \frac{b}{c} + 1$$,即$$\cos A = \frac{b}{c}$$。
2. 由余弦定理,$$\cos A = \frac{b^2 + c^2 - a^2}{2bc} = \frac{b}{c}$$,化简得$$b^2 + c^2 - a^2 = 2b^2$$,即$$c^2 = a^2 + b^2$$,故为直角三角形。
答案:B.直角三角形
7. 圆心角$$\angle AOB = 1$$弧度,$$AB = 2$$,求弧长。
解析:
1. 设半径为$$r$$,弦长公式$$AB = 2r \sin \frac{\theta}{2}$$,即$$2 = 2r \sin 0.5$$,故$$r = \frac{1}{\sin 0.5}$$。
2. 弧长$$l = r \theta = \frac{1}{\sin 0.5} \times 1 = \frac{1}{\sin 0.5}$$。
答案:A.$$\frac{1}{\sin 0.5}$$
8. 已知锐角$$\theta$$的终边经过点$$P(m, \sqrt{3})$$且$$\cos \theta = \frac{m}{2}$$,求函数$$g(x)$$的对称中心。
解析:
1. 由$$\cos \theta = \frac{m}{2}$$,且$$r = \sqrt{m^2 + 3} = 2$$,解得$$m = 1$$,故$$\theta = \frac{\pi}{3}$$。
2. 函数$$f(x) = 1 + \sin 2x$$,平移后$$g(x) = 1 + \sin \left(2x - \frac{2\pi}{3}\right)$$。
3. 对称中心满足$$2x - \frac{2\pi}{3} = k\pi$$,取$$k=0$$,得$$x = \frac{\pi}{3}$$,$$g\left(\frac{\pi}{3}\right) = 1$$。
答案:C.$$(\frac{\pi}{3}, 1)$$
9. 若$$\frac{\cos 2\alpha}{\cos \left(\frac{\pi}{4} + \alpha\right)} = \frac{1}{2}$$,求$$\cos \alpha + \sin \alpha$$。
解析:
1. 利用余弦倍角公式,$$\cos 2\alpha = \cos^2 \alpha - \sin^2 \alpha$$。
2. 设$$\cos \alpha + \sin \alpha = t$$,则$$\cos 2\alpha = t^2 - 1$$。
3. 代入原式,$$\frac{t^2 - 1}{\frac{\sqrt{2}}{2} (\cos \alpha - \sin \alpha)} = \frac{1}{2}$$,化简得$$t = \frac{1}{2}$$。
答案:A.$$\frac{1}{2}$$
10. 函数$$f(x)$$的解析式。
解析:
1. 观察图像,函数在$$x=0$$附近有奇异性,且整体形状符合选项B的特征。
2. 选项B的函数$$f(x) = \left(x - \frac{1}{x}\right) \left[\sin^2 \left(\frac{\pi}{4} - x\right) - \frac{1}{2}\right]$$,符合图像的振荡和渐近行为。
答案:B.$$f(x) = \left(x - \frac{1}{x}\right) \left[\sin^2 \left(\frac{\pi}{4} - x\right) - \frac{1}{2}\right]$$
.jpg)