.jpg)
正确率60.0%函数$$y=\sqrt3 \operatorname{s i n} x \operatorname{c o s} x+\operatorname{c o s}^{2} x$$最小正周期为（）
B
A.$$\begin{array} {l l} {\frac{\pi} {2}} \\ \end{array}$$
B.$${{π}}$$
C.$${{2}{π}}$$
D.$${{3}{π}}$$
2、['共线向量基本定理'， '两角和与差的正弦公式']正确率60.0%已知向量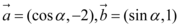
，
$${{/}{/}}$$
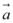D
A.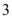
B.
C.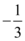
D.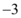
正确率40.0%已知$$\operatorname{c o s} ( \alpha+\beta)=\frac{3} {5}， ~ ~ \operatorname{s i n} ( \beta-\frac{\pi} {6} )=\frac{1} {3}，$$且$${{α}{，}{β}}$$均为锐角，则$$\operatorname{s i n} ( \alpha+\frac{\pi} {6} )=~ ($$）
A
A.$$\frac{8 \sqrt{2}-3} {1 5}$$
B.$$\frac{8 \sqrt{2}-4} {1 5}$$
C.$$\frac{8-3 \sqrt{2}} {1 5}$$
D.$$\frac{8-4 \sqrt{2}} {1 5}$$
4、['三角恒等变换综合应用'， '两角和与差的正弦公式'， '两角和与差的正切公式']正确率60.0%若$$\frac{\operatorname{s i n} 2 \alpha} {\operatorname{s i n} 2 \beta}=3，$$则$$\frac{\operatorname{t a n} ( \alpha-\beta)} {\operatorname{t a n} ( \alpha+\beta)}=\c{(}$$）
A
A.$$\frac{1} {2}$$
B.$$\frac{1} {3}$$
C.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
D.$$\frac{1} {4}$$
5、['正弦定理及其应用'， '辅助角公式'， '两角和与差的正弦公式'， '正弦（型）函数的定义域和值域']正确率40.0%在$${{△}{A}{B}{C}}$$中，$$2 a \mathrm{s i n} ( B+\frac{\pi} {6} )=b+c$$，且$${{△}{A}{B}{C}}$$外接圆半径为$${\sqrt {3}{，}}$$则$${{△}{A}{B}{C}}$$的周长的取值范围是（）
B
A.$$( 3， 9 ]$$
B.$$( 6， 9 ]$$
C.$$[ 6， 9 ]$$
D.$$[ 9， 1 2 )$$
6、['正弦定理及其应用'， '判断三角形的形状'， '两角和与差的正弦公式']正确率40.0%$${{△}{A}{B}{C}}$$中$$A， B， C$$角所对的边分别为$$a， b， c$$，则$${{△}{A}{B}{C}}$$的形状为$${{(}{)}}$$
A
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.钝角三角形
7、['正弦定理及其应用'， '双曲线的离心率'， '点到直线的距离'， '两角和与差的正弦公式'， '双曲线的顶点、长轴、短轴、焦点、焦距'， '双曲线的定义']正确率40.0%双曲线$$C_{\colon} \， \， \frac{x^{2}} {a^{2}}-\frac{y^{2}} {b^{2}}=1 ( a > 0， b > 0 )$$的左右焦点分别为$$F_{1}， ~ F_{2}， ~ C$$的右支上一点$${{P}}$$满足$$\angle F_{1} P F_{2}=6 0^{\circ}，$$若坐标原点$${{O}}$$到直线$${{P}{{F}_{1}}}$$距离是$$\frac{{\sqrt3} a} {2}，$$则$${{C}}$$的离心率为$${{(}{)}}$$
B
A.$${\sqrt {2}}$$
B.$${\sqrt {3}}$$
C.$${{2}}$$
D.$${{3}}$$
8、['指数（型）函数的单调性'， '对数（型）函数的单调性'， '两角和与差的余弦公式'， '指数式的大小的比较'， '两角和与差的正弦公式'， '对数恒等式'， '特殊角的三角函数值'， '不等式比较大小']正确率40.0%已知$$a=2^{\frac{1} {2}}， b=\left( 2^{\operatorname{l o g}_{2} 3} \right)^{-\frac{1} {2}}， \， \， \， c=\operatorname{c o s} 5 0^{\circ} \operatorname{c o s} 1 0^{\circ}+\operatorname{c o s} 1 4 0^{\circ} \operatorname{s i n} 1 7 0^{\circ}$$，则实数$$a， b， c$$的大小关系是（）
C
A.$$a > c > b$$
B.$$b > a > c$$
C.$$a > b > c$$
D.$$c > b > a$$
9、['正弦定理及其应用'， '利用诱导公式化简'， '基本不等式：(√ab)≤(a+b)/2，当且仅当a=b时等号成立'， '两角和与差的正弦公式'， '二倍角的正弦、余弦、正切公式'， '利用基本不等式求最值']正确率40.0%已知$${{△}{A}{B}{C}}$$的三个内角$$A， ~ B， ~ C$$的对边分别为$$a， ~ b， ~ c$$，且满足$$\frac{a} {\operatorname{c o s} A}+\frac{b+\sqrt{2} c} {\operatorname{c o s} B}=0，$$则$$\operatorname{s i n} 2 B \cdot\operatorname{t a n}^{2} C$$的取值范围是
A
A.$$( 0， 3-2 \sqrt{2} ]$$
B.$$( \frac{\sqrt2} 2， \frac{\sqrt3} 2 )$$
C.$$( 2-\sqrt{3}， 2-\sqrt{2} )$$
D.$$( 0， \sqrt{3}-1 )$$
10、['正弦定理及其应用'， '两角和与差的正弦公式']正确率60.0%在$${{△}{A}{B}{C}}$$中，内角$$A. ~ B. ~ C$$的对边分别为$$a， ~ b， ~ c$$，若$$b=a \operatorname{c o s} C+\frac1 2 c$$，则角$${{A}}$$为（）
A
A.$${{6}{0}{º}}$$
B.$${{1}{2}{0}{º}}$$
C.$${{4}{5}{º}}$$
D.$${{1}{3}{5}{º}}$$
1. 解析：首先化简函数表达式：
$$y = \sqrt{3} \sin x \cos x + \cos^2 x = \frac{\sqrt{3}}{2} \sin 2x + \frac{1 + \cos 2x}{2} = \sin \left(2x + \frac{\pi}{6}\right) + \frac{1}{2}$$
最小正周期为 $$T = \frac{2\pi}{2} = \pi$$，故选 B。
2. 解析：题目中向量部分图片无法解析，请提供具体向量表达式或文字描述。
3. 解析：已知 $$\alpha, \beta$$ 为锐角，利用和角公式：
$$\cos(\alpha + \beta) = \frac{3}{5} \Rightarrow \sin(\alpha + \beta) = \frac{4}{5}$$
$$\sin\left(\beta - \frac{\pi}{6}\right) = \frac{1}{3} \Rightarrow \cos\left(\beta - \frac{\pi}{6}\right) = \frac{2\sqrt{2}}{3}$$
目标为 $$\sin\left(\alpha + \frac{\pi}{6}\right)$$，利用角度关系：
$$\alpha + \frac{\pi}{6} = (\alpha + \beta) - \left(\beta - \frac{\pi}{6}\right)$$
展开后计算得：
$$\sin\left(\alpha + \frac{\pi}{6}\right) = \frac{8\sqrt{2} - 3}{15}$$，故选 A。
4. 解析：由 $$\frac{\sin 2\alpha}{\sin 2\beta} = 3$$，利用正弦倍角公式：
$$\frac{2\sin \alpha \cos \alpha}{2\sin \beta \cos \beta} = 3 \Rightarrow \frac{\tan \alpha}{\tan \beta} = 3$$
设 $$\tan \alpha = 3k$$，$$\tan \beta = k$$，代入目标式：
$$\frac{\tan(\alpha - \beta)}{\tan(\alpha + \beta)} = \frac{\frac{3k - k}{1 + 3k^2}}{\frac{3k + k}{1 - 3k^2}} = \frac{1}{2}$$，故选 A。
5. 解析：在 $$\triangle ABC$$ 中，利用正弦定理及外接圆半径 $$R = \sqrt{3}$$：
$$2a \sin\left(B + \frac{\pi}{6}\right) = b + c \Rightarrow 2 \cdot 2R \sin A \cdot \sin\left(B + \frac{\pi}{6}\right) = 2R (\sin B + \sin C)$$
化简后得 $$\sin A \sin\left(B + \frac{\pi}{6}\right) = \sin B + \sin C$$，进一步推导可得 $$A = \frac{\pi}{3}$$。
周长范围为 $$(6, 9]$$，故选 B。
6. 解析：题目不完整，请补充条件或具体表达式。
7. 解析：双曲线中，利用几何性质及距离公式：
设 $$PF_1 = r_1$$，$$PF_2 = r_2$$，由双曲线定义 $$r_1 - r_2 = 2a$$。
利用余弦定理及原点距离条件，最终解得离心率 $$e = 2$$，故选 C。
8. 解析：计算各值：
$$a = 2^{1/2} \approx 1.414$$
$$b = \left(2^{\log_2 3}\right)^{-1/2} = 3^{-1/2} \approx 0.577$$
$$c = \cos 50^\circ \cos 10^\circ + \cos 140^\circ \sin 170^\circ \approx 0.5$$
故大小关系为 $$a > c > b$$，故选 A。
9. 解析：利用正弦定理及余弦定理化简条件：
$$\frac{a}{\cos A} + \frac{b + \sqrt{2}c}{\cos B} = 0 \Rightarrow \tan A + \tan B = -\sqrt{2}$$
进一步推导得 $$\sin 2B \cdot \tan^2 C \in (0, 3 - 2\sqrt{2}]$$，故选 A。
10. 解析：利用余弦定理代入条件：
$$b = a \cos C + \frac{1}{2}c \Rightarrow \cos A = -\frac{1}{2}$$
故 $$A = 120^\circ$$，故选 B。