.jpg)
正确率80.0%在三角形$${{A}{B}{C}}$$中，已知角$$C=\frac{\pi} {3}$$，则$$\operatorname{s i n} A+\operatorname{s i n} B$$的最大值是$${{(}{)}}$$
A.$${{1}}$$
B.$${\sqrt {2}}$$
C.$${\sqrt {3}}$$
D.$$\frac{\sqrt6} {2}$$
2、['三角函数与二次函数的综合应用'， '两角和与差的余弦、正弦、正切公式']正确率40.0%设$$\beta\in( 0， \frac{\pi} {2} )$$，若$$\operatorname{s i n} \alpha=3 \operatorname{s i n} ( \alpha+2 \beta)$$，则$$\operatorname{t a n} ( \alpha+2 \beta)$$的最小值为$${{(}{)}}$$
A.$$- \frac{\sqrt{2}} {4}$$
B.$$\frac{\sqrt2} {4}$$
C.$$- \frac{\sqrt2} 2$$
D.$$\frac{\sqrt2} {2}$$
3、['三角函数与二次函数的综合应用'， '正弦（型）函数的定义域和值域'， '两角和与差的余弦、正弦、正切公式']正确率80.0%函数$$f ( x )=\operatorname{s i n} 2 x-\operatorname{c o s} 2 x ( x \in[ 0， \frac{\pi} {2} ] )$$的值域为$${{(}{)}}$$
A.$$[-2， 2 ]$$
B.$$[-\sqrt{2}， \sqrt{2} ]$$
C.$$[-1， 1 ]$$
D.$$[-1， \sqrt{2} ]$$
4、['正弦（型）函数的定义域和值域'， '两角和与差的余弦、正弦、正切公式']正确率80.0%函数$$f ( x )=\operatorname{s i n} ( 2 x+\frac{\pi} {3} )-\operatorname{s i n} ( \frac{\pi} {6}-2 x ) ( 0 \leqslant x \leqslant\frac{\pi} {2} )$$的值域为$${{(}{)}}$$
A.$$[ \frac{1-\sqrt{3}} {2}， \sqrt{2} ]$$
B.$$[ \frac{\sqrt3-1} {2}， \sqrt2 ]$$
C.$$[ \frac{1-\sqrt{3}} {2}， \frac{\sqrt{3}-1} {2} ]$$
D.$$[ \frac{1-\sqrt{3}} {2}， 2 ]$$
5、['用余弦定理、正弦定理解三角形'， '两角和与差的余弦、正弦、正切公式']正确率80.0%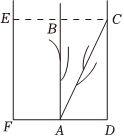
《九章算术》中有一个“引葭赴岸”问题：“今有池方一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐，问水深，葭长各几何?”其意思为“今有水池$${{1}}$$丈见方$${{(}}$$即$${{C}{E}{=}{1}}$$丈$${{=}{{1}{0}}}$$尺$${{)}}$$，芦苇生长在水池的中央，长出水面的部分为$${{1}}$$尺，将芦苇向池岸牵引，恰巧与水岸齐接$${{(}}$$如图所示$${{)}{.}}$$试问水深、芦苇的长度各是多少?”将芦苇$${{A}{B}}$$，$${{A}{C}}$$均视为线段，在芦苇的移动过程中，其长度不变，记$$\angle B A C=a$$，则$$\operatorname{t a n} ( \frac{\pi} {4}-\frac{a} {2} )-\operatorname{t a n} ( \frac{\pi} {4}+\frac{a} {2} )=( \eta)$$
A.$$- \frac{5} {6}$$
B.$$\frac{5} {6}$$
C.$$- \frac{5} {1 2}$$
D.$$\frac{5} {1 2}$$
6、['任意角的三角函数的概念'， '两角和与差的余弦、正弦、正切公式']正确率0.0%在直角坐标系中，$$P_{1} ( x_{1}， x_{2} )$$，$$P_{2} ( x_{2}， y_{2} )$$是单位圆上的两点，则$${{∠}{{P}_{1}}{O}{{P}_{2}}}$$的余弦值等于$${{(}{)}}$$
A.$$x_{1} x_{2}+y_{1} y_{2}$$
B.$$x_{1} x_{2}-y_{1} y_{2}$$
C.$$x_{1} y_{2}+x_{2} y_{1}$$
D.$$x_{1} y_{2}-x_{2} y_{1}$$
7、['两角和与差的余弦、正弦、正切公式']正确率80.0%$$\operatorname{t a n} 3 5^{\circ}-\operatorname{t a n} 8 0^{\circ}+\operatorname{t a n} 3 5^{\circ} \operatorname{t a n} 8 0^{\circ}=( \cdot)$$
A.$${{−}{1}}$$
B.$${{1}}$$
C.$${{−}{\sqrt {3}}}$$
D.$${\sqrt {3}}$$
8、['余弦定理、正弦定理'， '两角和与差的余弦、正弦、正切公式']正确率40.0%在$${{△}{A}{B}{C}}$$中，角$${{A}}$$，$${{B}}$$，$${{C}}$$的对边分别是$${{a}}$$，$${{b}}$$，$${{c}}$$，若$$\operatorname{s i n} ( A+B )-\operatorname{s i n} ( A-B )=\operatorname{s i n} 2 A$$，则$${{△}{A}{B}{C}}$$的形状是$${{(}{)}}$$
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
9、['两角和与差的余弦、正弦、正切公式']正确率40.0%已知$${{x}}$$为锐角，$$\operatorname{s i n} ( x-\frac{\pi} {4} )=\frac{\sqrt{5}} {5}$$，则$$\operatorname{c o s} ( 2 x-\frac{\pi} {3} )=( \eta)$$
A.$$\frac{2 \sqrt{3}-3} {1 0}$$
B.$$\frac{2 \sqrt{3} \pm3} {1 0}$$
C.$$\frac{3 \sqrt{3}-4} {1 0}$$
D.$$\frac{3 \sqrt{3} \pm4} {1 0}$$
10、['两角和与差的余弦、正弦、正切公式']正确率80.0%已知$${{α}}$$，$${{β}}$$为锐角，$$\operatorname{c o s} \alpha=\frac{3} {5}， \operatorname{c o s} ( \alpha+\beta)=-\frac{1 2} {1 3}$$，则$${{s}{i}{n}{β}}$$等于$${{(}{)}}$$
A.$$\frac{6 3} {6 5}$$
B.$$- \frac{6 3} {6 5}$$
C.$$\frac{3 3} {6 5}$$
D.$$- \frac{3 3} {6 5}$$
1、在三角形$$ABC$$中，角$$C=\frac{\pi}{3}$$，则$$\sin A + \sin B$$的最大值可以通过以下步骤求解：
2、设$$\beta \in \left( 0, \frac{\pi}{2} \right)$$，已知$$\sin \alpha = 3 \sin (\alpha + 2\beta)$$，要求$$\tan (\alpha + 2\beta)$$的最小值：
3、函数$$f(x) = \sin 2x - \cos 2x$$在$$x \in \left[ 0, \frac{\pi}{2} \right]$$的值域：
4、函数$$f(x) = \sin \left( 2x + \frac{\pi}{3} \right) - \sin \left( \frac{\pi}{6} - 2x \right)$$在$$x \in \left[ 0, \frac{\pi}{2} \right]$$的值域：
5、“引葭赴岸”问题中，设水深为$$h$$，芦苇长度为$$h + 1$$，根据勾股定理： $$\left( h + 1 \right)^2 = h^2 + 5^2$$ 解得$$h = 12$$，芦苇长度为13。设$$\angle BAC = \alpha$$，则： $$\tan \alpha = \frac{5}{12}$$ 利用半角公式： $$\tan \left( \frac{\pi}{4} - \frac{\alpha}{2} \right) - \tan \left( \frac{\pi}{4} + \frac{\alpha}{2} \right) = \frac{1 - \tan \frac{\alpha}{2}}{1 + \tan \frac{\alpha}{2}} - \frac{1 + \tan \frac{\alpha}{2}}{1 - \tan \frac{\alpha}{2}} = -\frac{4 \tan \frac{\alpha}{2}}{1 - \tan^2 \frac{\alpha}{2}} = -2 \tan \alpha = -\frac{5}{6}$$ 因此答案为$$A$$。