正确率40.0%已知$$\operatorname{t a n} \left( \alpha+\frac{\pi} {4} \right)=\frac{1} {2},$$且$$- \frac{\pi} {2} < \alpha< 0,$$则 $${\frac{2 \mathrm{s i n}^{2} \alpha+\mathrm{s i n} \, 2 \alpha} {\mathrm{c o s} \, \left( \alpha-{\frac{\pi} {4}} \right)}}=$$ ()
A
A.$$- \frac{2 \sqrt{5}} {5}$$
B.$$- \frac{3 \sqrt{5}} {1 0}$$
C.$$- \frac{3 \sqrt{1 0}} {1 0}$$
D.$$\frac{2 \sqrt{5}} {5}$$
2、['角α与π/2±α的三角函数值之间的关系', '两角和与差的余弦公式', '两角和与差的正弦公式']正确率60.0%$$\operatorname{c o s} 1 6^{\circ} \operatorname{c o s} 4 4^{\circ}-\operatorname{c o s} 7 4^{\circ} \operatorname{s i n} 4 4^{\circ}=$$()
C
A.$$\frac{\sqrt3} {2}$$
B.$$- \frac{\sqrt3} {2}$$
C.$$\frac{1} {2}$$
D.$$- \frac{1} {2}$$
3、['两角和与差的余弦公式', '同角三角函数的平方关系']正确率60.0%若$$\operatorname{c o s} \alpha=\frac{1} {5}, \, \, \alpha$$为锐角,则$$\operatorname{c o s} ~ \left( \alpha-\frac{\pi} {6} \right)=$$()
A
A.$$\frac{\sqrt3+2 \sqrt6} {1 0}$$
B.$$\frac{1+6 \sqrt{2}} {1 0}$$
C.$$\frac{6 \sqrt2-\sqrt3} {1 0}$$
D.$$\frac{6 \sqrt{2}-1} {1 0}$$
4、['两角和与差的余弦公式']正确率60.0%$$\operatorname{s i n} 1 5 5^{\circ} \mathrm{s i n} 3 5^{\circ}-\operatorname{c o s} 2 5^{\circ} \operatorname{c o s} 3 5^{\circ}=$$()
B
A.$$- \frac{\sqrt3} {2}$$
B.$$- \frac{1} {2}$$
C.$$\frac{1} {2}$$
D.$$\frac{\sqrt3} {2}$$
5、['给值求值', '两角和与差的余弦公式', '同角三角函数的平方关系']正确率60.0%已知$$\mathrm{c o s} \alpha+2 \mathrm{c o s} \beta=\sqrt{2},$$$$\operatorname{s i n} \alpha=2 \operatorname{s i n} \beta-\sqrt{3},$$则$$\operatorname{s i n}^{2} ( \alpha+\beta)=$$()
D
A.$$\frac{1} {2}$$
B.$$\frac{1} {4}$$
C.$${{0}}$$
D.$${{1}}$$
6、['两角和与差的余弦公式', '二倍角的正弦、余弦、正切公式', '同角三角函数的平方关系']正确率60.0%若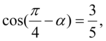 则
则 $${{(}{)}}$$
$${{(}{)}}$$
D
A.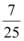
B.
C.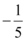
D.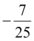
正确率40.0%$$\frac{2 \mathrm{s i n} 8 0^{\circ}-\mathrm{c o s} 7 0^{\circ}} {\mathrm{c o s} 2 0^{\circ}}=\mathrm{~ (}$$)
C
A.$${{−}{\sqrt {3}}}$$
B.$${{1}}$$
C.$${\sqrt {3}}$$
D.$${{2}}$$
8、['由图象(表)求三角函数的解析式', '正弦(型)函数的单调性', '函数图象的平移变换', '两角和与差的余弦公式', '辅助角公式', '三角函数的性质综合', '余弦(型)函数的单调性']正确率40.0%已知函数$$f \left( x \right)=\operatorname{c o s} \left( 4 x-\frac{\pi} {3} \right)+2 \operatorname{c o s}^{2} \left( 2 x \right)$$,将函数$${{y}{=}{f}{{(}{x}{)}}}$$的图象上所有点的横坐标伸长为原来的$${{2}}$$倍,纵坐标不变,再将所得函数图象向右平移$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$个单位,得到函数$${{y}{=}{g}{{(}{x}{)}}}$$的图象,则函数$${{y}{=}{g}{{(}{x}{)}}}$$的一个单调递增区间为()
B
A.$$[-\frac{\pi} {3}, \frac{\pi} {6} ]$$
B.$$[-\frac{\pi} {4}, \frac{\pi} {4} ]$$
C.$$[ \frac{\pi} {6}, \frac{2 \pi} {3} ]$$
D.$$\left[ \frac{\pi} {4}, \frac{3 \pi} {4} \right]$$
9、['两角和与差的余弦公式', '二倍角的正弦、余弦、正切公式', '同角三角函数的平方关系', '特殊角的三角函数值']正确率40.0%已知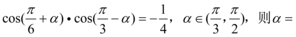 ()
()
D
A.$$\frac{7} {6} \pi$$
B.$$- \frac{\pi} {6}$$
C.$$- \frac{\pi} {4}$$
D.$$\frac{5} {1 2} \pi$$
10、['三角函数值在各象限的符号', '两角和与差的余弦公式', '同角三角函数的平方关系']正确率40.0%已知$$0 < ~ \alpha< ~ \beta$$,$$\beta\in( \frac{\pi} {2}, \pi)$$,$$\operatorname{s i n} \alpha=\frac{1} {2}$$,$$\operatorname{s i n} \beta=\frac{4} {5}$$,则$$\operatorname{c o s} ( \alpha-\beta)$$等于()
A
A.$$\frac{4-3 \sqrt{3}} {1 0}$$
B.$$\frac{4+3 \sqrt{3}} {1 0}$$
C.$$\frac{-4-3 \sqrt{3}} {1 0}$$
D.$$\frac{3 \sqrt{3}-4} {1 0}$$
1. 解析:
2. 解析:
3. 解析:
4. 解析:
5. 解析:
6. 解析:
7. 解析:
8. 解析:
9. 解析:
10. 解析:
.jpg)