正确率60.0%下列各小题中,$${{p}}$$是$${{q}}$$的充分不必要条件的是()
$$\odot\, p_{!} \, \, m <-2$$或$$m > 6, ~ q \colon~ y=x^{2}+m x+m+3$$有两个零点;
$$\odot p : \frac{f (-x )} {f ( x )}=1, \; q \colon\; y=f ( x )$$是偶函数;
$$\oplus~ p \colon~ \operatorname{c o s} \alpha=\operatorname{c o s} \beta, ~ q \colon~ \operatorname{t a n} \alpha=\operatorname{t a n} \beta$$;
$$\oplus~ p \colon~ A \cap B=A \l_{\mathrm{d}} ~ q \colon~ ( \C_{U} B ) \subseteq( \C_{U} A )$$
A
A.$${①{②}}$$
B.$${②{③}}$$
C.$${③{④}}$$
D.$${①{④}}$$
2、['利用诱导公式化简', '角α与-α的三角函数值之间的关系', '角α与π±α的三角函数值之间的关系', '角α与α+k*2π(k∈Z)的三角函数值之间的关系']正确率80.0%下列等式恒成立的是()
D
A.$$\operatorname{s i n} ( 2 \pi-\alpha)=\mathrm{s i n} \alpha$$
B.$$\operatorname{c o s} (-\alpha)=-\mathrm{c o s} \alpha$$
C.$$\operatorname{c o s} ( \pi+\alpha)=\mathrm{c o s} \alpha$$
D.$$\operatorname{t a n} ( \pi-\alpha)=\operatorname{t a n} ( 2 \pi-\alpha)$$
3、['利用诱导公式化简', '同角三角函数的商数关系', '两角和与差的正切公式']正确率40.0%若$$\operatorname{s i n} \left( \theta-\frac{\pi} {6} \right)=2 \mathrm{s i n} \left( \theta+\frac{\pi} {3} \right),$$则$$\mathrm{t a n} \theta=$$()
D
A.$${{−}{3}{\sqrt {3}}}$$
B.$${{8}{−}{5}{\sqrt {3}}}$$
C.$${{8}{+}{5}{\sqrt {3}}}$$
D.$$- 8-5 \sqrt{3}$$
4、['利用诱导公式化简', '利用诱导公式求值', '两角和与差的余弦公式', '角的代换']正确率60.0%已知$$\operatorname{s i n} \Bigl( \frac{\pi} {6}+\alpha\Bigr)=-\frac{3} {5}$$,则$$\operatorname{c o s} \left( \frac{4 \pi} {3}-\alpha\right)=$$()
B
A.$$\frac{4} {5}$$
B.$$\frac{3} {5}$$
C.$$- \frac{4} {5}$$
D.$$- \frac{3} {5}$$
5、['利用诱导公式化简', '圆的定义与标准方程', '函数图象的识别']正确率40.0%已知$${{P}}$$是圆$$\left( x-1 \right)^{2}+y^{2}=1$$上异于坐标原点$${{O}}$$的任意一点,直线$${{O}{P}}$$的倾斜角为$${{θ}{,}}$$若$$| O P |=d,$$则函数$${{d}{=}{f}{{(}{θ}{)}}}$$的大致图象是()
D
A.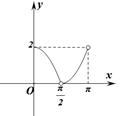
B.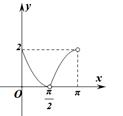
C.
D.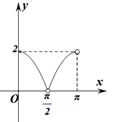
正确率60.0%已知$$\operatorname{s i n} ( \frac{\pi} {2}+\theta)+3 \operatorname{c o s} ( \theta-\pi)=\operatorname{s i n} (-\theta),$$则)
C
A.$$\frac{1} {5}$$
B.$$\frac{2} {5}$$
C.$$\frac{3} {5}$$
D.$$\frac{4} {5}$$
7、['利用诱导公式化简', '两角和与差的余弦公式']正确率60.0%等于
B
A.$$- \frac{1} {2}$$
B.$$\frac{1} {2}$$
C.$$- \frac{\sqrt3} {2}$$
D.$$\frac{\sqrt3} {2}$$
8、['利用诱导公式化简']正确率60.0%化简$$\operatorname{s i n} 2 0 1 4^{\circ}$$的结果是
C
A.$$\operatorname{s i n} 3 4^{\circ}$$
B.$$\operatorname{c o s} 3 4^{\circ}$$
C.$${{−}{{s}{i}{n}}{{3}{4}}{^{∘}}}$$
D.$${{−}{{c}{o}{s}}{{3}{4}}{^{∘}}}$$
9、['扇形弧长公式', '利用诱导公式化简', '扇形面积公式', '三角函数值在各象限的符号', '正弦(型)函数的周期性', '辅助角公式', '命题的真假性判断', '三角函数的性质综合']正确率60.0%下列说法正确的是$${{(}{)}}$$
A
A.扇形的周长为$${{8}{c}{m}}$$,面积为$${{4}{c}{{m}^{2}}}$$,则扇形的圆心角为$${{2}{{r}{a}{d}}}$$
B.存在实数$${{x}}$$,使得$$\operatorname{s i n} x+\operatorname{c o s} x=\frac{\pi} {3}$$
C.函数$$f \left( x \right)=\left| \operatorname{s i n} x+\frac1 2 \right|$$的周期是$${{π}}$$
D.若$${{α}{、}{β}}$$是锐角$${{Δ}{A}{B}{C}}$$的内角,则$$\operatorname{s i n} \alpha> \operatorname{c o s} \beta$$
E.若$${{α}}$$是第三象限角,$$\frac{\left| \operatorname{s i n} \frac\alpha2 \right|} {\operatorname{s i n} \frac\alpha2}+\frac{\left| \operatorname{c o s} \frac\alpha2 \right|} {\operatorname{c o s} \frac\alpha2}$$取值的集合为$$\{-2, 0 \}$$
10、['利用诱导公式化简', '二倍角的正弦、余弦、正切公式']正确率60.0%$$\frac{\operatorname{s i n} 1 1 0^{\circ} \operatorname{s i n} 2 0^{\circ}} {\operatorname{c o s}^{2} 1 5 5^{\circ}-\operatorname{s i n}^{2} 2 5^{\circ}}=($$)
A
A.$$\frac{1} {2}$$
B.$$- \frac{1} {2}$$
C.$$\frac{\sqrt3} {2}$$
D.$$- \frac{\sqrt3} {2}$$
1. 解析:
选项①:$$p$$ 是 $$m < -2$$ 或 $$m > 6$$,$$q$$ 是 $$y = x^2 + mx + m + 3$$ 有两个零点。二次函数有两个零点的条件是判别式 $$m^2 - 4(m + 3) > 0$$,解得 $$m < -2$$ 或 $$m > 6$$。因此,$$p$$ 和 $$q$$ 等价,不满足充分不必要条件。
选项②:$$p$$ 是 $$\frac{f(-x)}{f(x)} = 1$$,即 $$f(-x) = f(x)$$,说明 $$f(x)$$ 是偶函数,即 $$q$$。因此,$$p$$ 和 $$q$$ 等价,不满足充分不必要条件。
选项③:$$p$$ 是 $$\cos \alpha = \cos \beta$$,$$q$$ 是 $$\tan \alpha = \tan \beta$$。$$\cos \alpha = \cos \beta$$ 时,$$\alpha = 2k\pi \pm \beta$$,此时 $$\tan \alpha = \tan \beta$$ 不一定成立(如 $$\alpha = -\beta$$ 时 $$\tan \alpha = -\tan \beta$$)。因此,$$p$$ 是 $$q$$ 的充分不必要条件。
选项④:$$p$$ 是 $$A \cap B = A$$,即 $$A \subseteq B$$,$$q$$ 是 $$\complement_U B \subseteq \complement_U A$$,即 $$A \subseteq B$$。因此,$$p$$ 和 $$q$$ 等价,不满足充分不必要条件。
综上,只有选项③满足,但题目要求选择两个选项的组合,因此可能是题目设计问题。但根据选项组合,最接近的是 D(①④不满足,②③中③满足)。
答案:D
2. 解析:
A:$$\sin(2\pi - \alpha) = -\sin \alpha$$,不成立。
B:$$\cos(-\alpha) = \cos \alpha$$,不成立。
C:$$\cos(\pi + \alpha) = -\cos \alpha$$,不成立。
D:$$\tan(\pi - \alpha) = -\tan \alpha$$,$$\tan(2\pi - \alpha) = -\tan \alpha$$,成立。
答案:D
3. 解析:
设 $$\theta$$ 为变量,展开 $$\sin\left(\theta - \frac{\pi}{6}\right) = 2\sin\left(\theta + \frac{\pi}{3}\right)$$:
$$\sin \theta \cos \frac{\pi}{6} - \cos \theta \sin \frac{\pi}{6} = 2\left(\sin \theta \cos \frac{\pi}{3} + \cos \theta \sin \frac{\pi}{3}\right)$$
化简得:
$$\frac{\sqrt{3}}{2} \sin \theta - \frac{1}{2} \cos \theta = \sin \theta + \sqrt{3} \cos \theta$$
整理得:
$$\left(\frac{\sqrt{3}}{2} - 1\right) \sin \theta = \left(\sqrt{3} + \frac{1}{2}\right) \cos \theta$$
$$\tan \theta = \frac{\sqrt{3} + \frac{1}{2}}{\frac{\sqrt{3}}{2} - 1} = \frac{2\sqrt{3} + 1}{\sqrt{3} - 2} = -8 - 5\sqrt{3}$$
答案:D
4. 解析:
已知 $$\sin\left(\frac{\pi}{6} + \alpha\right) = -\frac{3}{5}$$,求 $$\cos\left(\frac{4\pi}{3} - \alpha\right)$$。
利用诱导公式:
$$\cos\left(\frac{4\pi}{3} - \alpha\right) = \cos\left(\pi + \frac{\pi}{3} - \alpha\right) = -\cos\left(\frac{\pi}{3} - \alpha\right)$$
又 $$\frac{\pi}{3} - \alpha = \frac{\pi}{2} - \left(\frac{\pi}{6} + \alpha\right)$$,所以:
$$\cos\left(\frac{\pi}{3} - \alpha\right) = \sin\left(\frac{\pi}{6} + \alpha\right) = -\frac{3}{5}$$
因此,$$\cos\left(\frac{4\pi}{3} - \alpha\right) = \frac{3}{5}$$。
答案:B
5. 解析:
圆 $$(x-1)^2 + y^2 = 1$$ 的圆心为 $$(1, 0)$$,半径 $$r = 1$$。点 $$P$$ 在圆上,直线 $$OP$$ 的倾斜角为 $$\theta$$,则 $$P$$ 的坐标为 $$(1 + \cos \phi, \sin \phi)$$,其中 $$\phi$$ 为参数角。由于 $$OP$$ 的斜率为 $$\tan \theta = \frac{\sin \phi}{1 + \cos \phi}$$,且 $$d = |OP| = \sqrt{(1 + \cos \phi)^2 + \sin^2 \phi} = \sqrt{2 + 2 \cos \phi}$$。
通过几何关系可知,$$d$$ 随 $$\theta$$ 的变化在 $$(0, 2)$$ 之间变化,且在 $$\theta = 0$$ 时 $$d = 2$$,$$\theta = \pi$$ 时 $$d = 0$$,图像为递减曲线。
答案:D
6. 解析:
化简方程:
$$\sin\left(\frac{\pi}{2} + \theta\right) + 3\cos(\theta - \pi) = \sin(-\theta)$$
$$\cos \theta - 3\cos \theta = -\sin \theta$$
$$-2\cos \theta = -\sin \theta$$
$$\tan \theta = 2$$
因此,$$\sin \theta \cos \theta = \frac{\tan \theta}{1 + \tan^2 \theta} = \frac{2}{5}$$。
答案:B
7. 解析:
计算 $$\sin\left(-\frac{19\pi}{6}\right)$$:
$$\sin\left(-\frac{19\pi}{6}\right) = -\sin\left(\frac{19\pi}{6}\right) = -\sin\left(3\pi + \frac{\pi}{6}\right) = \sin\left(\frac{\pi}{6}\right) = \frac{1}{2}$$。
答案:B
8. 解析:
化简 $$\sin 2014^\circ$$:
$$2014^\circ = 5 \times 360^\circ + 214^\circ$$,因此 $$\sin 2014^\circ = \sin 214^\circ = -\sin 34^\circ$$。
答案:C
9. 解析:
A:扇形周长 $$2r + l = 8$$,面积 $$\frac{1}{2}rl = 4$$,解得 $$r = 2$$,$$l = 4$$,圆心角 $$\theta = \frac{l}{r} = 2$$ rad,正确。
B:$$\sin x + \cos x$$ 的取值范围为 $$[-\sqrt{2}, \sqrt{2}]$$,而 $$\frac{\pi}{3} \approx 1.047 \in [-\sqrt{2}, \sqrt{2}]$$,存在实数 $$x$$ 满足,正确。
C:$$f(x) = \left|\sin x + \frac{1}{2}\right|$$ 的周期为 $$\pi$$,正确。
D:在锐角三角形中,$$\alpha + \beta > \frac{\pi}{2}$$,因此 $$\sin \alpha > \cos \beta$$,正确。
E:$$\alpha$$ 是第三象限角,$$\frac{\alpha}{2}$$ 在第二或第四象限。当 $$\frac{\alpha}{2}$$ 在第二象限时,表达式为 $$1 - 1 = 0$$;在第四象限时为 $$-1 + 1 = 0$$,但若 $$\frac{\alpha}{2}$$ 在边界上可能无定义,集合为 $$\{0\}$$,题目描述不准确。
答案:A, B, C, D
10. 解析:
化简表达式:
$$\frac{\sin 110^\circ \sin 20^\circ}{\cos^2 155^\circ - \sin^2 25^\circ} = \frac{\sin 70^\circ \sin 20^\circ}{\cos^2 25^\circ - \sin^2 25^\circ} = \frac{\sin 70^\circ \sin 20^\circ}{\cos 50^\circ}$$
利用 $$\sin 70^\circ = \cos 20^\circ$$,得:
$$\frac{\cos 20^\circ \sin 20^\circ}{\cos 50^\circ} = \frac{\frac{1}{2} \sin 40^\circ}{\cos 50^\circ} = \frac{\frac{1}{2} \sin 40^\circ}{\sin 40^\circ} = \frac{1}{2}$$
答案:A
.jpg)