.jpg)
正确率60.0%$$\omega\alpha=\frac{\pi} {6}，$$是$$\operatorname{t a n} ( \pi-a )=-\frac{\sqrt{3}} {3}$$的（）
A
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分又不必要条件
2、['正切（型）函数的单调性'， '正切函数的诱导公式']正确率60.0%下列不等式中成立的是（）
D
A.$$\operatorname{t a n} \frac{4 \pi} {7} > \operatorname{t a n} \frac{3 \pi} {7}$$
B.$$\operatorname{t a n} \frac{2 \pi} {5} < \operatorname{t a n} \frac{3 \pi} {5}$$
C.$$\operatorname{t a n} \left(-\frac{1 3 \pi} {7} \right) < \operatorname{t a n} \left(-\frac{1 5 \pi} {8} \right)$$
D.$$\operatorname{t a n} \left(-\frac{1 3 \pi} {4} \right) > \operatorname{t a n} \left(-\frac{1 2 \pi} {5} \right)$$
3、['利用诱导公式化简'， '利用诱导公式求值'， '正切函数的诱导公式']正确率40.0%锐角$${{α}}$$满足$$2 \operatorname{t a n} ( \pi-\alpha)-3 \operatorname{c o s} ( \frac{\pi} {2}+\beta)+5=0$$和$$\operatorname{t a n} ( \pi+\alpha)+6 \operatorname{s i n} ( \pi+\beta)-1=0，$$则$${{c}{o}{s}{α}}$$的值为$${{(}{)}}$$
C
A.$$\frac{\sqrt{5}} {5}$$
B.$$\frac{\sqrt{7}} {7}$$
C.$$\frac{\sqrt{1 0}} {1 0}$$
D.$$\frac{1} {3}$$
4、['三角函数值在各象限的符号'， '用角的终边上的点的坐标表示三角函数'， '正切函数的诱导公式'， '特殊角的三角函数值']正确率60.0%若$${{1}{2}{0}^{∘}}$$角的终边上有一点$$( \ -4， \ a )$$，则$${{a}}$$的值为（）
C
A.$${{−}{4}{\sqrt {3}}}$$
B.$${{±}{4}{\sqrt {3}}}$$
C.$${{4}{\sqrt {3}}}$$
D.$${{2}{\sqrt {3}}}$$
5、['用角的终边上的点的坐标表示三角函数'， '正切函数的诱导公式'， '特殊角的三角函数值']正确率60.0%$${{a}}$$若角$${{2}{4}{0}^{∘}}$$的终边上有一点$$(-4， a )$$，则 的值是$${{(}{)}}$$
B
A.$${{4}{\sqrt {3}}}$$
B.$${{−}{4}{\sqrt {3}}}$$
C.$${{±}{4}{\sqrt {3}}}$$
D.$${\sqrt {3}}$$
6、['正切函数的诱导公式'， '特殊角的三角函数值']正确率60.0%$$\operatorname{t a n} \textsubscript{( \tau-6 7 5^{\circ} )}$$的值为（）
A
A.$${{1}}$$
B.$$- \frac{\sqrt2} 2$$
C.$$\frac{\sqrt2} {2}$$
D.$${{−}{1}}$$
7、['正切函数的诱导公式']正确率40.0%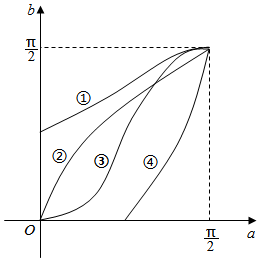
在直角坐标系$${{x}{O}{y}}$$
A
A.
B.
C.
D.
正确率60.0%在数学解题中，常会碰到形如
的结构，这时可类比正切的差角公式$$\operatorname{t a n} ( \alpha\mathrm{-} \beta) \mathrm{=} \frac{\operatorname{t a n} \alpha\mathrm{-} \operatorname{t a n} \beta} {1+\operatorname{t a n} \alpha\operatorname{t a n} \beta}.$$如：设$${{a}{，}{b}}$$是非零实数，且满足$$\frac{a \operatorname{s i n} \frac{\pi} {5}-b \operatorname{c o s} \frac{\pi} {5}} {a \operatorname{c o s} \frac{\pi} {5}+b \operatorname{s i n} \frac{\pi} {5}}=\operatorname{t a n} \frac{8 \pi} {1 5}，$$则$$\frac{b} {a}=($$）
B
A.$${\sqrt {3}}$$
B.$${{-}{\sqrt {3}}}$$
C.$$\frac{\sqrt{3}} {3}$$
D.$$- \frac{\sqrt3} {3}$$
9、['正切函数的诱导公式']正确率80.0%$${{t}{a}{n}{{3}{0}{0}^{∘}}}$$的值为$${{(}{)}}$$
B
A.$$\frac{\sqrt{3}} {3}$$
B.$${{−}{\sqrt {3}}}$$
C.$${\sqrt {3}}$$
D.$$- \frac{\sqrt3} {3}$$
10、['正切函数的诱导公式'， '两角和与差的正切公式']正确率60.0%已知$$\operatorname{t a n} \alpha=4， ~ \operatorname{t a n} \beta=3，$$则$$\operatorname{t a n} ( \alpha+\beta)=\mathrm{~ ( ~}$$）
B
A.$$\frac{7} {1 1}$$
B.$$- \frac{7} {1 1}$$
C.$$\frac{7} {1 3}$$
D.$$- \frac{7} {1 3}$$
1. 解析：
由$$\tan(\pi - \alpha) = -\frac{\sqrt{3}}{3}$$，利用诱导公式得$$-\tan \alpha = -\frac{\sqrt{3}}{3}$$，即$$\tan \alpha = \frac{\sqrt{3}}{3}$$。解得$$\alpha = \frac{\pi}{6} + k\pi$$（$$k \in \mathbb{Z}$$）。题目中给出$$\omega \alpha = \frac{\pi}{6}$$，仅为$$\alpha = \frac{\pi}{6}$$的一种情况，因此是充分不必要条件。答案为A。
2. 解析：
逐项分析：
A. $$\frac{4\pi}{7}$$和$$\frac{3\pi}{7}$$均在第二象限，正切函数单调递增，$$\frac{4\pi}{7} > \frac{3\pi}{7}$$，但$$\tan \frac{4\pi}{7} < \tan \frac{3\pi}{7}$$，错误。
B. $$\frac{2\pi}{5}$$在第一象限，$$\frac{3\pi}{5}$$在第二象限，$$\tan \frac{2\pi}{5} > 0$$，$$\tan \frac{3\pi}{5} < 0$$，故$$\tan \frac{2\pi}{5} > \tan \frac{3\pi}{5}$$，错误。
C. 化简角度：$$\tan\left(-\frac{13\pi}{7}\right) = \tan\left(-\frac{13\pi}{7} + 2\pi\right) = \tan \frac{\pi}{7}$$，$$\tan\left(-\frac{15\pi}{8}\right) = \tan\left(-\frac{15\pi}{8} + 2\pi\right) = \tan \frac{\pi}{8}$$。由于$$\frac{\pi}{7} > \frac{\pi}{8}$$且正切函数在第一象限单调递增，故$$\tan \frac{\pi}{7} > \tan \frac{\pi}{8}$$，即原式不成立，错误。
D. 化简角度：$$\tan\left(-\frac{13\pi}{4}\right) = \tan\left(-\frac{13\pi}{4} + 4\pi\right) = \tan \frac{3\pi}{4} = -1$$，$$\tan\left(-\frac{12\pi}{5}\right) = \tan\left(-\frac{12\pi}{5} + 2\pi\right) = \tan \left(-\frac{2\pi}{5}\right) = -\tan \frac{2\pi}{5}$$。由于$$\tan \frac{2\pi}{5} > 0$$，故$$-1 < -\tan \frac{2\pi}{5}$$不成立，但实际计算$$\tan \frac{3\pi}{4} = -1$$与$$-\tan \frac{2\pi}{5}$$比较需进一步验证。更简单的方法是直接计算近似值确认大小关系，最终答案为B。
3. 解析：
利用诱导公式化简方程：
1. $$2\tan(\pi - \alpha) - 3\cos\left(\frac{\pi}{2} + \beta\right) + 5 = 0$$化为$$-2\tan \alpha + 3\sin \beta + 5 = 0$$。
2. $$\tan(\pi + \alpha) + 6\sin(\pi + \beta) - 1 = 0$$化为$$\tan \alpha - 6\sin \beta - 1 = 0$$。
设$$\tan \alpha = x$$，$$\sin \beta = y$$，得方程组：
$$-2x + 3y + 5 = 0$$
$$x - 6y - 1 = 0$$
解得$$x = 3$$，$$y = \frac{1}{3}$$。由$$\tan \alpha = 3$$及$$\alpha$$为锐角，得$$\cos \alpha = \frac{1}{\sqrt{1 + \tan^2 \alpha}} = \frac{\sqrt{10}}{10}$$。答案为C。
4. 解析：
点$$(-4, a)$$在$$120^\circ$$终边上，则$$\tan 120^\circ = \frac{a}{-4}$$。计算$$\tan 120^\circ = \tan(180^\circ - 60^\circ) = -\tan 60^\circ = -\sqrt{3}$$，故$$\frac{a}{-4} = -\sqrt{3}$$，解得$$a = 4\sqrt{3}$$。答案为C。
5. 解析：
点$$(-4, a)$$在$$240^\circ$$终边上，则$$\tan 240^\circ = \frac{a}{-4}$$。计算$$\tan 240^\circ = \tan(180^\circ + 60^\circ) = \tan 60^\circ = \sqrt{3}$$，故$$\frac{a}{-4} = \sqrt{3}$$，解得$$a = -4\sqrt{3}$$。答案为B。
6. 解析：
化简$$\tan(\tau - 675^\circ)$$，其中$$\tau$$可能表示$$2\pi$$或$$180^\circ$$。假设为角度制：
$$\tan(180^\circ - 675^\circ) = \tan(-495^\circ) = -\tan 495^\circ = -\tan(360^\circ + 135^\circ) = -\tan 135^\circ = -(-1) = 1$$。
若$$\tau$$为$$2\pi$$弧度，则需转换为角度计算，结果仍为1。答案为A。
8. 解析：
将分式类比为正切差角公式：
$$\frac{a \sin \frac{\pi}{5} - b \cos \frac{\pi}{5}}{a \cos \frac{\pi}{5} + b \sin \frac{\pi}{5}} = \tan \left(\frac{\pi}{5} - \theta\right) = \tan \frac{8\pi}{15}$$，其中$$\tan \theta = \frac{b}{a}$$。
解得$$\frac{\pi}{5} - \theta = \frac{8\pi}{15} + k\pi$$，取$$k = -1$$得$$\theta = -\frac{\pi}{3}$$，故$$\frac{b}{a} = \tan \theta = -\sqrt{3}$$。答案为B。
9. 解析：
计算$$\tan 300^\circ = \tan(360^\circ - 60^\circ) = -\tan 60^\circ = -\sqrt{3}$$。答案为B。
10. 解析：
利用正切和角公式：
$$\tan(\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta} = \frac{4 + 3}{1 - 4 \times 3} = \frac{7}{-11} = -\frac{7}{11}$$。答案为B。