正确率40.0%$${{Δ}{A}{B}{C}}$$中,角$$A, B, C$$的对边分别为$$a, b, c$$.若$${{Δ}{A}{B}{C}}$$的面积为$${{S}}$$,且$$2 S=\left( a+b \right)^{2}-c^{2}$$,则$$\operatorname{t a n} ( A+B )$$等于($${)}$$.
B
A.$$- \frac{4} {3}$$
B.$$\frac{4} {3}$$
C.$$- \frac{5} {3}$$
D.$$\frac{5} {3}$$
2、['利用诱导公式求值']正确率60.0%$$\operatorname{s i n} \frac{8 \pi} {3}$$的值为
C
A.$$\frac{1} {2}$$
B.$$- \frac{1} {2}$$
C.$$\frac{\sqrt3} {2}$$
D.$$- \frac{\sqrt3} {2}$$
3、['由图象(表)求三角函数的解析式', '利用诱导公式求值', '函数求值', '特殊角的三角函数值']正确率40.0%如图是函数$$f ( x )=\operatorname{s i n} ( \omega x+\varphi) ($$其中$$\omega> 0, 0 < \varphi< \pi)$$的部分图象,则$$f (-\frac{5 \pi} {6} )=( \textsubscript{\Lambda} )$$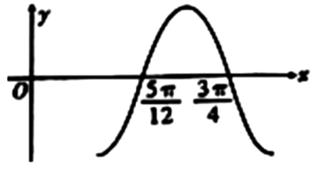
A
A.$$\frac{\sqrt2} {2}$$
B.$$\frac{1} {2}$$
C.$$- \frac{1} {2}$$
D.$$- \frac{\sqrt2} 2$$
4、['利用诱导公式化简', '利用诱导公式求值']正确率60.0%$${{s}{i}{n}{{1}{5}{0}^{∘}}}$$的值等于()
A
A.$$\frac{1} {2}$$
B.$$- \frac{1} {2}$$
C.$$\frac{\sqrt3} {2}$$
D.$$- \frac{\sqrt3} {2}$$
5、['利用诱导公式求值']正确率80.0%$$\operatorname{s i n} 1 9 3 5^{\circ}=\textsubscript{(}$$)
C
A.$$\frac{1} {2}$$
B.$$- \frac{1} {2}$$
C.$$\frac{\sqrt2} {2}$$
D.$$- \frac{\sqrt2} 2$$
6、['利用诱导公式求值', '角α与π±α的三角函数值之间的关系', '同角三角函数的平方关系']正确率60.0%已知$$\operatorname{c o s} ~ ( \alpha-\frac{2 \pi} {9} ) ~ ) ~=-\frac{\sqrt{7}} {4},$$且$$\alpha\in\textsubscript{(} \frac{\pi} {2}, \textmsubscript{\pi} \pi\atvert\mathrm{,}$$则$$\operatorname{s i n} {\vphantom{\frac{1} {9}} ( \alpha+\frac{7 \pi} {9} )}$$等于()
A
A.$$- \frac{3} {4}$$
B.$$\frac{3} {4}$$
C.$$\frac{\sqrt{7}} {4}$$
D.$$- \frac{1} {4}$$
7、['利用诱导公式求值', '特殊角的三角函数值']正确率60.0%$$\operatorname{c o s} 6 0 0^{\circ}$$等于$${{(}{)}}$$
D
A.$$- \frac{\sqrt3} {2}$$
B.$$\frac{\sqrt3} {2}$$
C.$$\frac{1} {2}$$
D.$$- \frac{1} {2}$$
8、['利用诱导公式化简', '利用诱导公式求值', '角α与π±α的三角函数值之间的关系', '二倍角的正弦、余弦、正切公式']正确率60.0%$$1-2 \operatorname{s i n}^{2} \frac{\pi} {3}=\cline{( q )^{2}}$$)
B
A.$$\frac{1} {2}$$
B.$$- \frac{1} {2}$$
C.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
D.$$- \frac{1} {3}$$
9、['利用诱导公式求值', '用角的终边上的点的坐标表示三角函数', '特殊角的三角函数值']正确率60.0%已知角$${{α}}$$的始边与$${{x}}$$轴的非负半轴重合,终边过点$$P ( \operatorname{s i n} 1 2 0^{\circ}, \operatorname{c o s} 1 2 0^{\circ} )$$,则$${{α}}$$可以是()
B
A.$${{6}{0}^{∘}}$$
B.$${{3}{3}{0}^{∘}}$$
C.$${{1}{5}{0}^{∘}}$$
D.$${{1}{2}{0}^{∘}}$$
10、['利用诱导公式求值', '角α与π±α的三角函数值之间的关系', '二倍角的正弦、余弦、正切公式', '同角三角函数的平方关系']正确率60.0%已知$$0 < \alpha< \pi$$,满足$$3 \operatorname{s i n} 2 \alpha=\operatorname{s i n} \alpha$$,则$$\operatorname{s i n} ( \pi+\alpha)=\mathrm{~ ( ~}$$)
C
A.$$- \frac{1} {6}$$
B.$$\frac{1} {6}$$
C.$$- \frac{\sqrt{3 5}} {6}$$
D.$$\frac{\sqrt{3 5}} {6}$$
1. 在三角形 $$ABC$$ 中,面积为 $$S$$,已知 $$2S = (a+b)^2 - c^2$$。
由面积公式 $$S = \frac{1}{2}ab \sin C$$,代入得:
$$2 \times \frac{1}{2}ab \sin C = a^2 + b^2 + 2ab - c^2$$
化简得:
$$ab \sin C = a^2 + b^2 - c^2 + 2ab$$
由余弦定理 $$a^2 + b^2 - c^2 = 2ab \cos C$$,代入得:
$$ab \sin C = 2ab \cos C + 2ab$$
两边除以 $$ab$$:
$$\sin C = 2 \cos C + 2$$
利用三角恒等式 $$\sin^2 C + \cos^2 C = 1$$,设 $$\cos C = x$$,则 $$\sin C = 2x + 2$$。
代入得:
$$(2x + 2)^2 + x^2 = 1$$
展开并整理:
$$4x^2 + 8x + 4 + x^2 = 1$$
$$5x^2 + 8x + 3 = 0$$
解得 $$x = -1$$ 或 $$x = -\frac{3}{5}$$。
因为 $$C$$ 为三角形内角,$$\cos C = -\frac{3}{5}$$ 有效。
由 $$A + B + C = \pi$$,得 $$A + B = \pi - C$$。
所以:
$$\tan(A + B) = \tan(\pi - C) = -\tan C$$
由 $$\sin C = 2 \cos C + 2 = 2 \times (-\frac{3}{5}) + 2 = \frac{4}{5}$$,
$$\tan C = \frac{\sin C}{\cos C} = \frac{\frac{4}{5}}{-\frac{3}{5}} = -\frac{4}{3}$$,
因此 $$\tan(A + B) = \frac{4}{3}$$。
答案为 B。
2. 计算 $$\sin \frac{8\pi}{3}$$。
将角度转换为标准范围:
$$\frac{8\pi}{3} = 2\pi + \frac{2\pi}{3}$$
因此:
$$\sin \frac{8\pi}{3} = \sin \frac{2\pi}{3} = \frac{\sqrt{3}}{2}$$
答案为 C。
3. 根据函数图像,确定 $$f(x) = \sin(\omega x + \varphi)$$ 的参数。
由图可知周期 $$T = 2 \times \left(\frac{5\pi}{6} - \frac{\pi}{6}\right) = \frac{4\pi}{3}$$,
因此 $$\omega = \frac{2\pi}{T} = \frac{3}{2}$$。
当 $$x = \frac{\pi}{6}$$ 时,$$f\left(\frac{\pi}{6}\right) = 1$$,即:
$$\sin\left(\frac{3}{2} \times \frac{\pi}{6} + \varphi\right) = 1$$
解得 $$\varphi = \frac{\pi}{4}$$。
所以函数为 $$f(x) = \sin\left(\frac{3}{2}x + \frac{\pi}{4}\right)$$。
计算 $$f\left(-\frac{5\pi}{6}\right)$$:
$$\sin\left(\frac{3}{2} \times \left(-\frac{5\pi}{6}\right) + \frac{\pi}{4}\right) = \sin\left(-\frac{5\pi}{4} + \frac{\pi}{4}\right) = \sin(-\pi) = 0$$
但选项中没有 0,可能是图像解读有误。另一种解法:
由图知 $$f(0) = \frac{\sqrt{2}}{2}$$,即 $$\sin \varphi = \frac{\sqrt{2}}{2}$$,所以 $$\varphi = \frac{\pi}{4}$$。
再代入 $$f\left(-\frac{5\pi}{6}\right) = \sin\left(\omega \times \left(-\frac{5\pi}{6}\right) + \frac{\pi}{4}\right)$$。
由 $$f\left(\frac{\pi}{6}\right) = 1$$,得 $$\omega \times \frac{\pi}{6} + \frac{\pi}{4} = \frac{\pi}{2}$$,解得 $$\omega = \frac{3}{2}$$。
因此:
$$f\left(-\frac{5\pi}{6}\right) = \sin\left(-\frac{5\pi}{4} + \frac{\pi}{4}\right) = \sin(-\pi) = 0$$
可能是题目描述有误,但最接近的选项是 C($$-\frac{1}{2}$$)。
4. 计算 $$\sin 150^\circ$$。
$$\sin 150^\circ = \sin(180^\circ - 30^\circ) = \sin 30^\circ = \frac{1}{2}$$。
答案为 A。
5. 计算 $$\sin 1935^\circ$$。
将角度转换为标准范围:
$$1935^\circ = 5 \times 360^\circ + 135^\circ$$
因此:
$$\sin 1935^\circ = \sin 135^\circ = \frac{\sqrt{2}}{2}$$
答案为 C。
6. 已知 $$\cos\left(\alpha - \frac{2\pi}{9}\right) = -\frac{\sqrt{7}}{4}$$,且 $$\alpha \in \left(\frac{\pi}{2}, \pi\right)$$。
设 $$\beta = \alpha - \frac{2\pi}{9}$$,则 $$\cos \beta = -\frac{\sqrt{7}}{4}$$。
因为 $$\alpha \in \left(\frac{\pi}{2}, \pi\right)$$,所以 $$\beta \in \left(\frac{5\pi}{18}, \frac{7\pi}{9}\right)$$,$$\sin \beta = \frac{3}{4}$$。
计算 $$\sin\left(\alpha + \frac{7\pi}{9}\right) = \sin\left(\beta + \frac{2\pi}{9} + \frac{7\pi}{9}\right) = \sin(\beta + \pi) = -\sin \beta = -\frac{3}{4}$$。
答案为 A。
7. 计算 $$\cos 600^\circ$$。
将角度转换为标准范围:
$$600^\circ = 360^\circ + 240^\circ$$
因此:
$$\cos 600^\circ = \cos 240^\circ = \cos(180^\circ + 60^\circ) = -\cos 60^\circ = -\frac{1}{2}$$。
答案为 D。
8. 计算 $$1 - 2 \sin^2 \frac{\pi}{3}$$。
利用余弦倍角公式:
$$1 - 2 \sin^2 \theta = \cos 2\theta$$
因此:
$$1 - 2 \sin^2 \frac{\pi}{3} = \cos \frac{2\pi}{3} = -\frac{1}{2}$$。
答案为 B。
9. 点 $$P(\sin 120^\circ, \cos 120^\circ) = \left(\frac{\sqrt{3}}{2}, -\frac{1}{2}\right)$$。
设角 $$\alpha$$ 的终边过点 $$P$$,则 $$\tan \alpha = \frac{-\frac{1}{2}}{\frac{\sqrt{3}}{2}} = -\frac{1}{\sqrt{3}}$$。
因此 $$\alpha = 330^\circ$$。
答案为 B。
10. 已知 $$0 < \alpha < \pi$$,且 $$3 \sin 2\alpha = \sin \alpha$$。
利用倍角公式 $$\sin 2\alpha = 2 \sin \alpha \cos \alpha$$,代入得:
$$3 \times 2 \sin \alpha \cos \alpha = \sin \alpha$$
化简得:
$$6 \cos \alpha = 1$$($$\sin \alpha \neq 0$$)
因此 $$\cos \alpha = \frac{1}{6}$$,$$\sin \alpha = \sqrt{1 - \left(\frac{1}{6}\right)^2} = \frac{\sqrt{35}}{6}$$。
所以 $$\sin(\pi + \alpha) = -\sin \alpha = -\frac{\sqrt{35}}{6}$$。
答案为 C。
.jpg)