1、['角α与π/2±α的三角函数值之间的关系', '函数图象的平移变换', '正弦曲线的定义']正确率60.0%已知$$f ( x )=\operatorname{s i n} \left( x+\frac{\pi} {2} \right),$$$$g ( x )=\operatorname{c o s} \Bigl( x-\frac{\pi} {2} \Bigr)$$,则$${{f}{(}{x}{)}}$$的图像()
D
A.与$${{g}{(}{x}{)}}$$的图像相同
B.与$${{g}{(}{x}{)}}$$的图像关于$${{y}}$$轴对称
C.向左平移$$\frac{\pi} {2}$$个单位长度得到$${{g}{(}{x}{)}}$$的图像
D.向右平移$$\frac{\pi} {2}$$个单位长度得到$${{g}{(}{x}{)}}$$的图像
2、['角α与π/2±α的三角函数值之间的关系', '给值求值', '同角三角函数基本关系的综合应用', '二倍角的正弦、余弦、正切公式']正确率60.0%已知$$\operatorname{s i n} \Bigl( \frac{\pi} {1 2}+\alpha\Bigr)=\frac{\sqrt{2}} {4},$$则$$\operatorname{s i n} \left( \frac{\pi} {3}-2 a \right)=$$()
B
A.$$\frac{\sqrt2} {4}$$
B.$$\frac{3} {4}$$
C.$$\frac{\sqrt{7}} {4}$$
D.$$- \frac{3} {4}$$
3、['角α与π/2±α的三角函数值之间的关系', '二倍角的正弦、余弦、正切公式']正确率40.0%已知$$\mathrm{s i n} 2 a=\frac{2} {3}$$,则$$c o s^{2} \left( a+\frac{\pi} {4} \right)=( ~ ~ )$$
A
A.$$\frac{1} {6}$$
B.$$\frac{1} {3}$$
C.$$\frac{1} {2}$$
D.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
4、['角α与π/2±α的三角函数值之间的关系', '三角函数值在各象限的符号', '同角三角函数的平方关系', '二倍角的正弦、余弦、正切公式']正确率60.0%已知$$\alpha\in\left(-\frac{\pi} {2}, 0 \right)$$,$$\operatorname{c o s} \left( \alpha-\frac{\pi} {2} \right)=-\frac{3} {5}$$,则$$\operatorname{s i n} 2 \alpha=$$()
C
A.$$\frac{1} {2 5}$$
B.$$\frac{2 4} {2 5}$$
C.$$- \frac{2 4} {2 5}$$
D.$$- \frac{1} {2 5}$$
5、['角α与π/2±α的三角函数值之间的关系', '余弦(型)函数的定义域和值域']正确率60.0%函数$$f ( x )=\frac{1} {3} \mathrm{s i n} ( x+\frac{\pi} {6} )+\operatorname{c o s} ( x-\frac{\pi} {3} )$$的最大值为()
A
A.$$\frac{4} {3}$$
B.$${{1}}$$
C.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
D.$$\frac{1} {3}$$
6、['角α与π/2±α的三角函数值之间的关系', '二倍角的正弦、余弦、正切公式']正确率60.0%已知$$\operatorname{c o s} ~ ( \alpha+\frac{\pi} {4} ) ~=\frac{1} {3},$$则$$\operatorname{s i n} 2 \alpha=$$()
B
A.$$- \frac{7} {9}$$
B.$$\begin{array} {l l} {7} \\ {\frac{7} {9}} \\ \end{array}$$
C.$$\pm\frac{2 \sqrt{2}} {3}$$
D.$$\pm\frac{7} {9}$$
7、['函数奇偶性的应用', '角α与π/2±α的三角函数值之间的关系', '函数奇、偶性的定义']正确率60.0%已知$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) \ =\left\{\begin{matrix} {\operatorname{c o s} \left( x+\alpha\right), x \geqslant0} \\ {\operatorname{s i n} \left( x+\beta\right), x < 0} \\ \end{matrix} \right.$$是奇函数,则$${{α}{,}{β}}$$的可能值为()
C
A.$$\alpha=\pi, \, \, \, \beta=\frac{\pi} {2}$$
B.$$\alpha=0, \, \, \, \beta=\frac{\pi} {2}$$
C.$$\alpha=\frac{\pi} {2}, \, \, \, \beta=\pi$$
D.$$\alpha=\frac{\pi} {2}, \, \, \, \beta=\frac{\pi} {2}$$
8、['利用诱导公式化简', '角α与π/2±α的三角函数值之间的关系', '探究φ对函数y=Asin(wx+φ)的图象的影响', '三角函数的图象变换']正确率60.0%要得到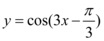 的图象,只需将函数
的图象,只需将函数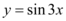 的图象()
的图象()
A
A.向左平移 个长度单位
个长度单位
B.向右平移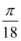 个长度单位
个长度单位
C.向左平移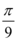 个长度单位
个长度单位
D.向右平移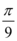 个长度单位
个长度单位
9、['利用诱导公式求值', '角α与π/2±α的三角函数值之间的关系', '同角三角函数的商数关系', '两角和与差的正弦公式', '同角三角函数基本关系的综合应用', '二倍角的正弦、余弦、正切公式']正确率40.0%若$$2 \operatorname{c o s}^{2} ( \frac{\pi} {4}-\frac{\alpha} {2}-\frac{\beta} {2} )=1+3 \operatorname{s i n} ( \alpha-\beta)$$,且 则$$\frac{\operatorname{t a n} \alpha} {\operatorname{t a n} \beta}=$$()
则$$\frac{\operatorname{t a n} \alpha} {\operatorname{t a n} \beta}=$$()
C
A.$${{1}}$$
B.$$\frac{1} {2}$$
C.$${{2}}$$
D.$${{3}}$$
10、['正弦(型)函数的单调性', '角α与π/2±α的三角函数值之间的关系', '不等式的解集与不等式组的解集', '三角函数的图象变换']正确率40.0%函数$${{f}{(}{x}{)}}$$的图象可看作是将函数$$y=2 \operatorname{c o s} x$$的图象向右平移$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$个单位后,再把图象上所有点的横坐标变为原来的$$\frac{1} {\omega} ( \omega> 0 )$$倍而得到的,若函数$${{f}{(}{x}{)}}$$在区间$$\left( \frac{\pi} {3}, \frac{4 \pi} {3} \right)$$上单调递减,则$${{ω}}$$的取值范围是 ()
B
A.$$[ \frac{1 9} {8}, \frac{5} {2} ]$$
B.$$[ \frac{1} {2}, \frac{7} {8} ]$$
C.$$\left( 0, \frac{5} {8} \right]$$
D.$$\left[ \frac{7} {8}, 1 \right]$$
1. 解析:
首先化简函数:$$f(x) = \sin\left(x + \frac{\pi}{2}\right) = \cos x$$,$$g(x) = \cos\left(x - \frac{\pi}{2}\right) = \sin x$$。显然,$$f(x)$$ 和 $$g(x)$$ 的图像不相同(A错误),也不关于 $$y$$ 轴对称(B错误)。将 $$f(x)$$ 向左平移 $$\frac{\pi}{2}$$ 个单位得到 $$\cos\left(x + \frac{\pi}{2}\right) = -\sin x$$,与 $$g(x)$$ 不符(C错误)。将 $$f(x)$$ 向右平移 $$\frac{\pi}{2}$$ 个单位得到 $$\cos\left(x - \frac{\pi}{2}\right) = \sin x = g(x)$$,故 D 正确。
2. 解析:
设 $$\theta = \frac{\pi}{12} + \alpha$$,则 $$\sin \theta = \frac{\sqrt{2}}{4}$$。目标式为 $$\sin\left(\frac{\pi}{3} - 2\alpha\right) = \sin\left(\frac{\pi}{2} - 2\theta\right) = \cos 2\theta$$。利用 $$\cos 2\theta = 1 - 2\sin^2 \theta = 1 - 2 \times \left(\frac{\sqrt{2}}{4}\right)^2 = \frac{3}{4}$$,故 B 正确。
3. 解析:
利用余弦平方公式:$$\cos^2\left(a + \frac{\pi}{4}\right) = \frac{1 + \cos\left(2a + \frac{\pi}{2}\right)}{2} = \frac{1 - \sin 2a}{2}$$。代入 $$\sin 2a = \frac{2}{3}$$,得 $$\frac{1 - \frac{2}{3}}{2} = \frac{1}{6}$$,故 A 正确。
4. 解析:
由 $$\cos\left(\alpha - \frac{\pi}{2}\right) = -\frac{3}{5}$$,得 $$\sin \alpha = -\frac{3}{5}$$。因 $$\alpha \in \left(-\frac{\pi}{2}, 0\right)$$,$$\cos \alpha = \sqrt{1 - \sin^2 \alpha} = \frac{4}{5}$$。故 $$\sin 2\alpha = 2 \sin \alpha \cos \alpha = 2 \times \left(-\frac{3}{5}\right) \times \frac{4}{5} = -\frac{24}{25}$$,C 正确。
5. 解析:
将函数化简:$$f(x) = \frac{1}{3} \sin\left(x + \frac{\pi}{6}\right) + \cos\left(x - \frac{\pi}{3}\right)$$。利用相位关系,$$\cos\left(x - \frac{\pi}{3}\right) = \sin\left(x + \frac{\pi}{6}\right)$$,因此 $$f(x) = \frac{4}{3} \sin\left(x + \frac{\pi}{6}\right)$$。最大值为 $$\frac{4}{3}$$,A 正确。
6. 解析:
由 $$\cos\left(\alpha + \frac{\pi}{4}\right) = \frac{1}{3}$$,平方得 $$\cos^2\left(\alpha + \frac{\pi}{4}\right) = \frac{1 + \cos\left(2\alpha + \frac{\pi}{2}\right)}{2} = \frac{1 - \sin 2\alpha}{2} = \frac{1}{9}$$。解得 $$\sin 2\alpha = \frac{7}{9}$$,但需注意符号。因 $$\cos\left(\alpha + \frac{\pi}{4}\right) = \frac{1}{3} > 0$$,$$\alpha + \frac{\pi}{4}$$ 可能在第一或第四象限,但 $$\sin 2\alpha$$ 的值唯一为 $$\frac{7}{9}$$,B 正确。
7. 解析:
函数为奇函数,需满足 $$f(0) = 0$$ 且 $$f(-x) = -f(x)$$。由 $$f(0) = \cos \alpha = 0$$,得 $$\alpha = \frac{\pi}{2} + k\pi$$。对于 $$x < 0$$,$$f(-x) = \sin(-x + \beta) = -\sin(x - \beta)$$,而 $$-f(x) = -\sin(x + \beta)$$。因此需 $$-\sin(x - \beta) = -\sin(x + \beta)$$,即 $$\sin(x - \beta) = \sin(x + \beta)$$,解得 $$\beta = k\pi$$。选项中满足条件的是 D($$\alpha = \frac{\pi}{2}$$,$$\beta = \frac{\pi}{2}$$)。
8. 解析:
目标函数为 $$y = \sin\left(2x + \frac{\pi}{3}\right)$$,原函数为 $$y = \sin 2x$$。将 $$y = \sin 2x$$ 向左平移 $$\frac{\pi}{6}$$ 个单位得到 $$y = \sin\left(2\left(x + \frac{\pi}{6}\right)\right) = \sin\left(2x + \frac{\pi}{3}\right)$$,故 A 正确。
9. 解析:
化简方程:$$2\cos^2\left(\frac{\pi}{4} - \frac{\alpha}{2} - \frac{\beta}{2}\right) = 1 + \cos\left(\frac{\pi}{2} - \alpha - \beta\right) = 1 + \sin(\alpha + \beta)$$。原方程变为 $$1 + \sin(\alpha + \beta) = 1 + 3\sin(\alpha - \beta)$$,即 $$\sin(\alpha + \beta) = 3\sin(\alpha - \beta)$$。展开得 $$\sin \alpha \cos \beta + \cos \alpha \sin \beta = 3(\sin \alpha \cos \beta - \cos \alpha \sin \beta)$$,整理得 $$\tan \alpha = 2 \tan \beta$$,故 $$\frac{\tan \alpha}{\tan \beta} = 2$$,C 正确。
10. 解析:
变换后的函数为 $$f(x) = 2\cos\left(\omega x - \frac{\pi}{6}\omega\right)$$。单调递减区间需满足 $$\pi + 2k\pi \leq \omega x - \frac{\pi}{6}\omega \leq 2\pi + 2k\pi$$,即 $$\frac{\pi}{\omega}\left(1 + \frac{\omega}{6} + 2k\right) \leq x \leq \frac{\pi}{\omega}\left(2 + \frac{\omega}{6} + 2k\right)$$。题目要求在 $$\left(\frac{\pi}{3}, \frac{4\pi}{3}\right)$$ 上递减,故需 $$\frac{\pi}{\omega}\left(1 + \frac{\omega}{6}\right) \leq \frac{\pi}{3}$$ 且 $$\frac{4\pi}{3} \leq \frac{\pi}{\omega}\left(2 + \frac{\omega}{6}\right)$$。解得 $$\omega \geq \frac{7}{8}$$ 且 $$\omega \leq 1$$,故 D 正确。
题目来源于各渠道收集,若侵权请联系下方邮箱
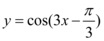 的图象,只需将函数
的图象,只需将函数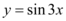 的图象()
的图象() 个长度单位
个长度单位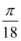 个长度单位
个长度单位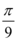 个长度单位
个长度单位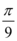 个长度单位
个长度单位则$$\frac{\operatorname{t a n} \alpha} {\operatorname{t a n} \beta}=$$()
.jpg)