正确率40.0%已知数列{$${{a}_{n}}$$}的前$${{n}}$$项和为$${{S}_{n}{,}}$$且 $$a_{1}=2, a_{n+1}=S_{n}$$ ,若$$a_{n} \in( 0, \ 2 0 2 0 ),$$则称项$${{a}_{n}}$$为“和谐项”,则数列{$${{a}_{n}}$$}的所有“和谐项”的平方和为()
A
A.$$\frac1 3 \times4^{1 1}+\frac8 3$$
B.$$\frac{1} {3} \times4^{1 1}-\frac{4} {3}$$
C.$$\frac{1} {3} \times4^{1 0}+\frac{8} {3}$$
D.$$\frac{1} {3} \times4^{1 2}-\frac{4} {3}$$
2、['等比数列的性质', '等比中项', '等比数列的基本量']正确率60.0%在各项均为正数的等比数列$${{\{}{{a}_{n}}{\}}}$$中,若$$a_{4} a_{6}=4, \, \, a_{8} a_{1 0}=1 6$$,则$$a_{2} a_{1 2}=($$)
A
A.$${{8}}$$
B.$${{1}{6}}$$
C.$${{3}{2}}$$
D.$${{6}{4}}$$
3、['等比数列前n项和的应用', '等比数列的基本量']正确率60.0%设等比数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和为$${{S}_{n}}$$,且$$a_{4}=2 a_{2}$$,则$$\frac{S_{8}} {S_{4}}$$等于()
B
A.$${{4}}$$
B.$${{5}}$$
C.$${{8}}$$
D.$${{9}}$$
4、['等差中项', '等比数列的基本量']正确率60.0%已知等比数列$${{\{}{{a}_{n}}{\}}}$$的各项都是正数,且$$3 a_{1}, ~ \frac{1} {2} a_{3}, ~ 2 a_{2}$$成等差数列,则$$\frac{a_{8}+a_{7}} {a_{5}+a_{4}}=($$)
C
A.$${{8}}$$
B.$${{9}}$$
C.$${{2}{7}}$$
D.$${{4}}$$
5、['等比数列的通项公式', '等比数列的基本量']正确率60.0%已知等比数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和为$$S_{n}, \, \, a_{1}+a_{3}=5, \, \, S_{4}=1 5$$,则$$S_{6}=( \textsubscript{\Lambda} )$$
D
A.$${{1}{5}}$$
B.$${{3}{1}}$$
C.$${{4}{0}}$$
D.$${{6}{3}}$$
6、['等比数列的基本量']正确率60.0%在等比数列 中,
中,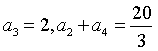 ,则公比
,则公比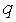 的值为$${{(}{)}}$$
的值为$${{(}{)}}$$
D
A.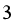
B.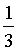
C. 或
或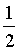
D.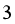 或
或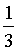
正确率40.0%已知等比数列$${{\{}{{a}_{n}}{\}}}$$的各项都为正数,且当$${{n}{⩾}{3}}$$时,$$a_{4} a_{2 n-4}=1 0^{2 n}$$,则数列$$\operatorname{l g} a_{1}, \; 2 \operatorname{l g} a_{2}, \; 2^{2} \operatorname{l g} a_{3}, \; 2^{3} \operatorname{l g} a_{4}, \; \; \cdots, \; 2^{n-1} \operatorname{l g} a_{n}, \; \; \cdots$$的前$${{n}}$$项和$${{S}_{n}}$$等于$${{(}{)}}$$
C
A.$${{n}{⋅}{{2}^{n}}}$$
B.$$( n-1 ) \cdot2^{n-1}-1$$
C.$$( n-1 ) \cdot2^{n}+1$$
D.$${{2}^{n}{+}{1}}$$
8、['等比数列的通项公式', '等比数列的定义与证明', '等比数列的基本量']正确率60.0%若公比$${{q}}$$不为$${{1}}$$的等比数列$${{\{}{{a}_{n}}{\}}}$$满足$$a_{n+2}+a_{n+1}=2 a_{n} ( n \in N * )$$,则$${{q}{=}{(}{)}}$$
C
A.$${{3}}$$
B.$${{2}}$$
C.$${{−}{2}}$$
D.$${{−}{1}}$$
9、['一元二次方程根与系数的关系', '数列的函数特征', '等比数列的通项公式', '等比数列的基本量']正确率40.0%在单调递减的等比数列$${{\{}{{a}_{n}}{\}}}$$中,已知$${{a}_{3}{,}{{a}_{5}}}$$为一元二次方程$$x^{2}-\frac{2 0} {8 1} x+\frac{4} {7 2 9}=0$$的两个根,则其前$${{n}}$$项和为()
C
A.$$\frac{3^{n}-1} {7 2 9}$$
B.$$\frac{3^{n+1}-1} {2 4 3}$$
C.$$\frac{3^{n}-1} {3^{n-1}}$$
D.$$\frac{3^{n+1}-1} {3^{n}}$$
10、['数列的函数特征', '等比数列的通项公式', '等比数列的基本量']正确率60.0%已知等比数列$${{\{}{{a}_{n}}{\}}}$$为单调递增数列,设其前$${{n}}$$项和为$${{S}_{n}}$$,若$$a_{2}=2, \, \, S_{3}=7$$,则$${{a}_{5}}$$的值为()
A
A.$${{1}{6}}$$
B.$${{3}{2}}$$
C.$${{8}}$$
D.$$\frac{1} {4}$$
1. 解析:
由题意得 $$a_{n+1} = S_n$$,且 $$a_1 = 2$$。当 $$n \geq 2$$ 时,$$a_n = S_{n-1}$$,因此 $$a_{n+1} - a_n = a_n$$,即 $$a_{n+1} = 2a_n$$。由此可得数列 $$\{a_n\}$$ 从第二项起为等比数列,公比为 2。通项公式为: $$a_n = \begin{cases} 2, & n=1 \\ 2^{n-1}, & n \geq 2 \end{cases}$$
“和谐项”满足 $$0 < a_n < 2020$$,即 $$2^{n-1} < 2020$$,解得 $$n \leq 11$$。因此“和谐项”为 $$a_1, a_2, \ldots, a_{11}$$,其平方和为: $$2^2 + \sum_{k=2}^{11} (2^{k-1})^2 = 4 + \sum_{k=1}^{10} 4^k = 4 + \frac{4(4^{10}-1)}{3} = \frac{1}{3} \times 4^{11} - \frac{4}{3}$$
答案为 B。
2. 解析:
设等比数列的公比为 $$q$$,由题意得: $$a_4 a_6 = a_5^2 = 4 \Rightarrow a_5 = 2$$ $$a_8 a_{10} = a_9^2 = 16 \Rightarrow a_9 = 4$$
因为 $$a_9 = a_5 q^4$$,即 $$4 = 2 q^4$$,解得 $$q^2 = \sqrt{2}$$。因此: $$a_2 a_{12} = a_7^2 = (a_5 q^2)^2 = (2 \times \sqrt{2})^2 = 8$$
答案为 A。
3. 解析:
设等比数列的公比为 $$q$$,由 $$a_4 = 2 a_2$$ 得: $$a_1 q^3 = 2 a_1 q \Rightarrow q^2 = 2$$
因此: $$\frac{S_8}{S_4} = \frac{a_1 (1-q^8)/(1-q)}{a_1 (1-q^4)/(1-q)} = \frac{1-q^8}{1-q^4} = 1 + q^4 = 1 + 4 = 5$$
答案为 B。
4. 解析:
设等比数列的公比为 $$q$$,由题意得: $$\frac{1}{2} a_3 = \frac{3a_1 + 2a_2}{2} \Rightarrow a_3 = 3a_1 + 2a_2$$
代入 $$a_2 = a_1 q$$ 和 $$a_3 = a_1 q^2$$ 得: $$a_1 q^2 = 3a_1 + 2a_1 q \Rightarrow q^2 - 2q - 3 = 0 \Rightarrow q = 3$$
因此: $$\frac{a_8 + a_7}{a_5 + a_4} = \frac{a_1 q^7 + a_1 q^6}{a_1 q^4 + a_1 q^3} = q^3 = 27$$
答案为 C。
5. 解析:
设等比数列的公比为 $$q$$,由题意得: $$a_1 + a_3 = a_1 (1 + q^2) = 5$$ $$S_4 = a_1 \frac{1-q^4}{1-q} = 15$$
解得 $$a_1 = 1$$,$$q = 2$$。因此: $$S_6 = \frac{1 \times (1-2^6)}{1-2} = 63$$
答案为 D。
6. 解析:
由题意得: $$\frac{a_5 + a_6}{a_1 + a_2} = \frac{a_1 q^4 + a_1 q^5}{a_1 + a_1 q} = q^4 = 16 \Rightarrow q = 2$$
答案为 B。
7. 解析:
由题意得 $$a_4 a_{2n-4} = 10^{2n}$$,设公比为 $$q$$,则: $$a_1 q^3 \cdot a_1 q^{2n-5} = 10^{2n} \Rightarrow (a_1 q^{n-1})^2 = 10^{2n} \Rightarrow a_n = 10^n$$
因此数列 $$\{2^{n-1} \lg a_n\}$$ 的通项为 $$2^{n-1} \cdot n$$,其前 $$n$$ 项和为: $$S_n = \sum_{k=1}^n k \cdot 2^{k-1} = (n-1) \cdot 2^n + 1$$
答案为 C。
8. 解析:
由递推式 $$a_{n+2} + a_{n+1} = 2a_n$$ 得: $$a_1 q^{n+1} + a_1 q^n = 2a_1 q^{n-1} \Rightarrow q^2 + q - 2 = 0 \Rightarrow q = -2$$
答案为 C。
9. 解析:
解方程 $$x^2 - \frac{20}{81}x + \frac{4}{729} = 0$$ 得两根为 $$\frac{2}{27}$$ 和 $$\frac{2}{9}$$。因为数列单调递减,所以 $$a_3 = \frac{2}{9}$$,$$a_5 = \frac{2}{27}$$。
设公比为 $$q$$,则 $$a_5 = a_3 q^2 \Rightarrow q = \frac{1}{\sqrt{3}}$$。因此: $$a_1 = \frac{a_3}{q^2} = \frac{2}{9} \times 3 = \frac{2}{3}$$
前 $$n$$ 项和为: $$S_n = \frac{\frac{2}{3} \left(1 - \left(\frac{1}{3}\right)^n\right)}{1 - \frac{1}{3}} = \frac{3^n - 1}{3^{n-1}}}$$
答案为 C。
10. 解析:
设等比数列的公比为 $$q$$,由题意得: $$a_2 = a_1 q = 2$$ $$S_3 = a_1 (1 + q + q^2) = 7$$
解得 $$a_1 = 1$$,$$q = 2$$。因此: $$a_5 = a_1 q^4 = 16$$
答案为 A。
.jpg)