正确率40.0%已知数列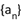 的前
的前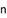 项和为
项和为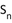 ,
,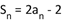 ,若存在两项
,若存在两项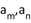 ,使得
,使得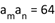 ,则
,则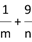 的最小值为$${{(}{)}}$$
的最小值为$${{(}{)}}$$
B
A.
B.
C.
D.
首先,根据题意,数列的前$$n$$项和为$$S_n$$,且满足$$S_n = 2a_n - 1$$。我们需要找到$$a_m \cdot a_n = 64$$时,$$\frac{1}{m} + \frac{9}{n}$$的最小值。
步骤1:求通项公式
已知$$S_n = 2a_n - 1$$,当$$n = 1$$时,$$S_1 = a_1 = 2a_1 - 1$$,解得$$a_1 = 1$$。
对于$$n \geq 2$$,有$$S_{n-1} = 2a_{n-1} - 1$$。因为$$S_n - S_{n-1} = a_n$$,所以:
$$a_n = 2a_n - 2a_{n-1}$$
整理得$$a_n = 2a_{n-1}$$。因此,数列$${a_n}$$是首项为1,公比为2的等比数列,通项公式为:
$$a_n = 2^{n-1}$$
步骤2:确定$$m$$和$$n$$的关系
根据题意,存在两项$$a_m$$和$$a_n$$使得$$a_m \cdot a_n = 64$$。代入通项公式:
$$2^{m-1} \cdot 2^{n-1} = 2^{m+n-2} = 64 = 2^6$$
因此,$$m + n - 2 = 6$$,即$$m + n = 8$$。
步骤3:求最小值
我们需要在$$m + n = 8$$的条件下,求$$\frac{1}{m} + \frac{9}{n}$$的最小值。
设$$m = x$$,则$$n = 8 - x$$($$x$$为正整数且$$1 \leq x \leq 7$$)。表达式变为:
$$f(x) = \frac{1}{x} + \frac{9}{8 - x}$$
为了找到最小值,我们计算$$f(x)$$的导数并求极值点:
$$f'(x) = -\frac{1}{x^2} + \frac{9}{(8 - x)^2}$$
令$$f'(x) = 0$$,解得:
$$-\frac{1}{x^2} + \frac{9}{(8 - x)^2} = 0$$
整理得:
$$\frac{9}{(8 - x)^2} = \frac{1}{x^2}$$
两边开平方得:
$$\frac{3}{8 - x} = \frac{1}{x}$$
解得$$x = 2$$。
验证$$x = 2$$时,$$f(2) = \frac{1}{2} + \frac{9}{6} = \frac{1}{2} + \frac{3}{2} = 2$$。
检查其他整数点:
- 当$$x = 1$$时,$$f(1) = 1 + \frac{9}{7} \approx 2.285$$;
- 当$$x = 3$$时,$$f(3) = \frac{1}{3} + \frac{9}{5} = \frac{5}{15} + \frac{27}{15} = \frac{32}{15} \approx 2.133$$。
因此,最小值出现在$$x = 2$$,即$$m = 2$$,$$n = 6$$时,最小值为2。
步骤4:选择正确答案
题目选项中的最小值为$$2$$,对应选项B。
最终答案为:$$\boxed{B}$$
题目来源于各渠道收集,若侵权请联系下方邮箱.jpg)