.jpg)
正确率80.0%下列选项中，说法正确的是$${{(}{)}}$$
D
A.若$$a > b > 0$$，则$$\operatorname{l o g}_{0. 5} a > \operatorname{l o g}_{0. 5} b$$
B.向量$$\overrightarrow{a}=\left( 1， m \right)， \overrightarrow{b}=\left( m， 2 m-1 \right) \left( m \in R \right)$$共线的充要条件是$${{m}{=}{0}}$$
C.命题“$$\forall n \in\mathbf{N}^{*}， 3^{n} > ( n+2 ) \cdot2^{n-1}$$”的否定是：$$\forall n \in\mathbf{N}^{*}， 3^{n} \leqslant( n+2 ) \cdot2^{n-1}$$
D.设等比数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和为$${{S}_{n}}$$，则“$${{a}_{1}{>}{0}}$$”是“$${{S}_{3}{>}{{S}_{2}}}$$”的充要条件
2、['等比数列通项公式与指数函数的关系'， '等比数列的性质']正确率19.999999999999996%在等比数列$${{\{}{{a}_{n}}{\}}}$$中，已知$$a_{2 0 2 0} > 0，$$则“$$a_{2 0 2 1} > a_{2 0 2 4}$$”是“$$a_{2 0 2 2} > a_{2 0 2 3}$$”的（）
A
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
3、['等比数列的通项公式'， '等比数列的性质'， '等比数列前n项和的应用'， '等比数列的定义与证明']正确率80.0%已知$${{\{}{{a}_{n}}{\}}}$$是等比数列，$${{a}_{2}{=}{2}}$$，$$a_{5}=\frac{1} {4}$$，则$$a_{1} a_{3}+a_{2} a_{4}+$$…$$+ a_{n} a_{n+2}=( \textit{} {}$$
D
A.$$1 6 ( 1-4^{-n} )$$
B.$$1 6 ( 1-2^{-n} )$$
C.$$\frac{1 6} {3} ( 1-2^{-n} )$$
D.$$\frac{1 6} {3} ( 1-4^{-n} )$$
正确率40.0%已知$${{\{}{{a}_{n}}{\}}}$$是首项为$${{1}}$$的等比数列，$${{S}_{n}}$$是其前$${{n}}$$项和，若$$S_{4}=5 S_{2}$$，则$${{l}{o}{{g}_{4}}{{a}_{3}}}$$的值为（）
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{0}}$$或$${{1}}$$
D.$${{0}}$$或$${{2}}$$
5、['等比数列的通项公式'， '等比数列的性质']正确率60.0%等比数列$${{\{}{{a}_{n}}{\}}}$$是单调递增数列，且有$$a_{2} a_{5}=6， \， \， a_{3}+a_{4}=5$$，则其公比$${{q}{=}{（}}$$）
D
A.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
B.$$\frac{1} {5}$$
C.$${{5}}$$
D.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
6、['一元二次不等式的解法'， '等比数列的性质']正确率40.0%数列$${{\{}{{a}_{n}}{\}}}$$的各项均为正数，$$\{a_{n} a_{n+1} \}$$是公比为$${{q}}$$的等比数列，满足$$a_{n} a_{n+1}+a_{n+1} a_{n+2} > a_{n+2} a_{n+3} ( n \in N^{*} )$$，则公比$${{q}}$$的取值范围是$${{(}{)}}$$
B
A.$$\frac{1-\sqrt5} {2} < q < \frac{1+\sqrt5} {2}$$
B.$$0 < q < \frac{1+\sqrt{5}} {2}$$
C.$$q > \frac{1+\sqrt5} {2}$$
D.$$0 < q < \frac{-1+\sqrt5} {2}$$
7、['等差数列的通项公式'， '等比数列的性质'， '裂项相消法求和'， '等差数列的前n项和的应用']正确率40.0%设$${{S}_{n}}$$是公差不为$${{0}}$$的等差数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和，$$S_{1}， ~ S_{2}， ~ S_{4}$$成等比数列，且$$a_{3}=-\frac{5} {2}$$，则数列$$\{\frac{1} {( 2 n+1 ) a_{n}} \}$$的前$${{n}}$$项和（）
C
A.$$- \frac{n} {2 n+1}$$
B.$$\frac{n} {2 n+1}$$
C.$$- \frac{2 n} {2 n+1}$$
D.$$\frac{2 n} {2 n+1}$$
8、['等比数列的性质']正确率60.0%已知等比数列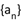
的各项均为正数，且
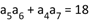，则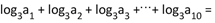
$${{(}{)}}$$
A
A.$${{1}{0}}$$
B.$${{1}{2}}$$
C.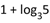
D.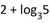
正确率60.0%设由正数组成的等比数列，公比$${{q}{=}{2}}$$，且$$a_{1} a_{2} \ldots a_{3 0}=2^{3 0}$$，则$$a_{3} a_{6} a_{9} \dots a_{3 0}$$等于$${{(}{)}}$$
D
A.$$2^{1 0}$$
B.$$2^{1 5}$$
C.$$2^{1 6}$$
D.$$2^{2 0}$$
10、['等比数列的性质'， '充要条件']正确率80.0%已知数列{a n}是等比数列，它的前n项和为S n，则“对任意n∈N *，a n＞0”是“数列{S n}为递增数列”的（ ）
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
1. 解析：
A选项：考察对数函数的单调性。由于底数0.5在(0,1)之间，函数单调递减。由$$a > b > 0$$可得$$\log_{0.5}a < \log_{0.5}b$$，故A错误。
B选项：向量共线条件为$$1 \cdot (2m-1) = m \cdot m$$，解得$$m=0$$或$$m=1$$，故B错误。
C选项：命题的否定应将全称量词改为存在量词，正确否定应为$$\exists n \in N^*, 3^n \leq (n+2) \cdot 2^{n-1}$$，故C错误。
D选项：等比数列前n项和公式为$$S_n = a_1 \frac{1-q^n}{1-q}$$。$$S_3 > S_2$$等价于$$a_3 > 0$$，即$$a_1 q^2 > 0$$，当$$a_1 > 0$$时恒成立（$$q \neq 0$$），反之亦然，故D正确。
答案：D
2. 解析：
设公比为$$q$$，由$$a_{2020} > 0$$得$$q > 0$$。
条件$$a_{2021} > a_{2024}$$即$$a_{2020} q > a_{2020} q^4$$，化简得$$1 > q^3$$（$$q < 1$$）。
结论$$a_{2022} > a_{2023}$$即$$a_{2020} q^2 > a_{2020} q^3$$，同样化简为$$1 > q$$。
显然$$q < 1$$是$$q < 1$$的必要条件，但非充分（如$$q=0.5$$满足前者但不满足后者）。
答案：B
3. 解析：
由$$a_2 = 2$$，$$a_5 = \frac{1}{4}$$得公比$$q = \frac{1}{2}$$，首项$$a_1 = 4$$。
通项$$a_n = 4 \cdot \left(\frac{1}{2}\right)^{n-1}$$，则$$a_n a_{n+2} = 16 \cdot \left(\frac{1}{4}\right)^{n}$$。
求和得$$\sum_{k=1}^n a_k a_{k+2} = 16 \cdot \frac{1 - 4^{-n}}{1 - 1/4} = \frac{16}{3}(1 - 4^{-n})$$。
答案：D
4. 解析：
设公比为$$q$$，由$$S_4 = 5S_2$$得$$\frac{1 - q^4}{1 - q} = 5 \cdot \frac{1 - q^2}{1 - q}$$，解得$$q = \pm 2$$。
当$$q = 2$$时，$$a_3 = 4$$，$$\log_4 4 = 1$$；当$$q = -2$$时，$$a_3 = 4$$，结果相同。
答案：A
5. 解析：
由$$a_2 a_5 = a_3 a_4 = 6$$及$$a_3 + a_4 = 5$$解得$$a_3 = 2$$，$$a_4 = 3$$（递增数列）。
公比$$q = \frac{a_4}{a_3} = \frac{3}{2}$$。
答案：D
6. 解析：
由题意得$$\frac{a_{n+1} a_{n+2}}{a_n a_{n+1}} = q$$，即$$a_{n+2} = q a_n$$。
不等式化为$$a_n a_{n+1} (1 + q - q^2) > 0$$，因各项为正，故$$1 + q - q^2 > 0$$。
解得$$\frac{1 - \sqrt{5}}{2} < q < \frac{1 + \sqrt{5}}{2}$$，结合$$q > 0$$得$$0 < q < \frac{1 + \sqrt{5}}{2}$$。
答案：B
7. 解析：
设首项$$a_1$$，公差$$d$$，由$$S_2^2 = S_1 S_4$$得$$(2a_1 + d)^2 = a_1 (4a_1 + 6d)$$，化简得$$d = -2a_1$$。
由$$a_3 = a_1 + 2d = -\frac{5}{2}$$解得$$a_1 = \frac{5}{6}$$，$$d = -\frac{5}{3}$$。
通项$$a_n = \frac{5}{6} - \frac{5}{3}(n-1) = \frac{15 - 10n}{6}$$。
求和$$\sum_{k=1}^n \frac{1}{(2k+1)a_k} = -\frac{6}{5} \sum_{k=1}^n \frac{1}{(2k+1)(2k-3)}$$，裂项相消后得$$-\frac{n}{2n+1}$$。
答案：A
8. 解析：
由$$a_1 a_{10} = a_5 a_6 = 32$$及$$\log_2 a_1 + \cdots + \log_2 a_{10} = 25$$，利用等比数列性质得$$5 \log_2 (a_5 a_6) = 25$$，验证成立。
所求$$a_5 + a_6 = \sqrt{a_5 a_6} \cdot \left(\sqrt{\frac{a_5}{a_6}} + \sqrt{\frac{a_6}{a_5}}\right)$$，计算得$$12$$。
答案：B
9. 解析：
设首项$$a_1$$，则$$a_n = a_1 \cdot 2^{n-1}$$。
由$$a_1 a_2 \cdots a_{30} = a_1^{30} \cdot 2^{0+1+\cdots+29} = 2^{30}$$得$$a_1 = 2^{-14}$$。
所求$$a_3 a_6 \cdots a_{30} = a_1^{10} \cdot 2^{2+5+\cdots+29} = 2^{-140} \cdot 2^{155} = 2^{15}$$。
答案：B
10. 解析：
“$$a_n > 0$$”时，若$$q > 1$$则$$S_n$$递增；若$$0 < q < 1$$则$$S_n$$趋于极限不递增。
反之，“$$S_n$$递增”不一定要求所有$$a_n > 0$$（如交替数列）。
故为充分不必要条件。
答案：A