.jpg)
正确率60.0%等差数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和为$${{S}_{n}}$$，若$${{S}_{5}{=}{{3}{5}}}$$，点$$A ( 3， a_{3} )$$与$$B ( 5， a_{5} )$$都在斜率为$${{−}{2}}$$的直线$${{l}}$$上，则使$${{S}_{n}}$$取得最大值的$${{n}}$$值为（）
A
A.$${{6}}$$
B.$${{7}}$$
C.$${{5}{，}{6}}$$
D.$${{7}{，}{8}}$$
2、['等差数列的通项公式']正确率80.0%已知等差数列$${{\{}{{a}_{n}}{\}}}$$满足$$4 a_{3}=3 a_{2}，$$则$${{\{}{{a}_{n}}{\}}}$$中一定为零的项是（）
A
A.$${{a}_{6}}$$
B.$${{a}_{4}}$$
C.$$a_{1 0}$$
D.$$a_{1 2}$$
3、['等差数列的通项公式'， '等差数列通项公式与一次函数的关系']正确率40.0%在等差数列$${{\{}{{a}_{n}}{\}}}$$中，$$a_{1} > 0， 5 a_{5}=1 7 a_{9}$$，则数列$${{\{}{{a}_{n}}{\}}}$$前$${{n}}$$项和$${{S}_{n}}$$取最大值时，$${{n}}$$的值等于$${{(}{)}}$$
C
A.$${{1}{2}}$$
B.$${{1}{1}}$$
C.$${{1}{0}}$$
D.$${{9}}$$
4、['等差数列的通项公式']正确率40.0%在等差数列$${{\{}{{a}_{n}}{\}}}$$中，若$$a_{1}+2 a_{2}+3 a_{3}=1 8$$，则$$2 a_{1}+a_{5}=( \textit{} {} {} )$$
A
A.$${{9}}$$
B.$${{8}}$$
C.$${{6}}$$
D.$${{3}}$$
5、['等差数列的通项公式'， '等差数列的基本量'， '等差数列的前n项和的应用']正确率60.0%据有关文献记载：我国古代一座$${{9}}$$层塔共挂了$${{1}{2}{6}}$$盏灯，且相邻两层中的下一层灯数比上一层灯数都多$${{n}{(}{n}}$$为常数)盏，底层的灯数是顶层的$${{1}{3}}$$倍，则塔的底层共有灯（）
C
A.$${{2}}$$盏
B.$${{3}}$$盏
C.$${{2}{6}}$$盏
D.$${{2}{7}}$$盏
6、['等差数列的通项公式'， '等比中项']正确率60.0%已知等差数列$${{\{}{{a}_{n}}{\}}}$$的公差为$${{4}}$$，且$$a_{2} \，， \， \， a_{3} \，， \， \， a_{6}$$成等比数列，则$$a_{1 0}=( \eta)$$
B
A.$${{3}{8}}$$
B.$${{3}{4}}$$
C.$${{3}{0}}$$
D.$${{2}{6}}$$
7、['等差数列的通项公式']正确率60.0%在等差数列$${{\{}{{a}_{n}}{\}}}$$中，已知$$a_{2}=1， ~ a_{8}=1 3$$，则公差$${{d}{=}{（}}$$）
B
A.$${{3}}$$
B.$${{2}}$$
C.$${{4}}$$
D.$${{5}}$$
8、['等差数列的通项公式'， '等比数列的通项公式'， '公式法求和'， '等比数列的基本量'， '对数的运算性质'， '等差数列的前n项和的应用'， '二次函数的图象分析与判断']正确率40.0%在各项均为正数的等比数列$${{\{}{{a}_{n}}{\}}}$$中，公比
，若$$a_{3}+a_{5}=1 0， \， \， a_{2} \cdot a_{6}=1 6$$，数列$${{\{}{{b}_{n}}{\}}}$$的前$${{n}}$$项和为$${{S}_{n}}$$，且$$b_{n}=l o g_{2} a_{n}$$，则当$$\frac{S_{1}} 1+\frac{S_{2}} 2+\ldots+\frac{S_{n}} n$$取得最大值时，$${{n}}$$的值为（）
D
A.$${{9}}$$
B.$${{1}{0}}$$
C.$${{9}}$$或$${{1}{0}}$$
D.$${{1}{0}}$$或$${{1}{1}}$$
9、['等差数列的通项公式'， '等差数列的定义与证明'， '等差数列的基本量'， '等差数列的前n项和的性质']正确率40.0%在数列$${{\{}{{a}_{n}}{\}}}$$中，$$a_{n+1}-a_{n}=2， \， \， S_{n}$$为$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和．若$$S_{1 0}=5 0$$，则数列$$\{a_{n}+a_{n+1} \}$$的前$${{1}{0}}$$项和为（）
C
A.$${{1}{0}{0}}$$
B.$${{1}{1}{0}}$$
C.$${{1}{2}{0}}$$
D.$${{1}{3}{0}}$$
10、['等差数列的通项公式'， '数列中的数学文化问题'， '等差数列的性质']正确率60.0%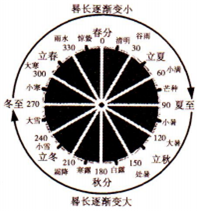
我国古代著名的$${《}$$
B
A.$$9 5 3 \frac{1} {3}$$分
B.$$1 0 5 2 \mathrm{\frac{1} {2}}$$分
C.$$1 1 5 1 \frac2 3$$分
D.$$1 2 5 0 \frac{5} {6}$$分
1. 解析：
已知等差数列 $$\{a_n\}$$ 的前 $$n$$ 项和为 $$S_n$$，且 $$S_5 = 35$$。点 $$A(3, a_3)$$ 和 $$B(5, a_5)$$ 在斜率为 $$-2$$ 的直线 $$l$$ 上。
步骤：
1. 由直线斜率公式：$$\frac{a_5 - a_3}{5 - 3} = -2$$，得 $$a_5 - a_3 = -4$$。
2. 等差数列性质：$$a_5 - a_3 = 2d = -4$$，故公差 $$d = -2$$。
3. 利用 $$S_5 = 35$$：$$S_5 = \frac{5}{2}(2a_1 + 4d) = 35$$，解得 $$a_1 = 11$$。
4. 通项公式：$$a_n = 11 + (n-1)(-2) = 13 - 2n$$。
5. 前 $$n$$ 项和公式：$$S_n = \frac{n}{2}(2a_1 + (n-1)d) = -n^2 + 12n$$。
6. 求最大值：$$S_n$$ 为二次函数，顶点在 $$n = 6$$，验证 $$S_6 = 36$$，$$S_7 = 35$$，因此 $$n = 6$$ 时 $$S_n$$ 最大。
答案： A
2. 解析：
已知等差数列 $$\{a_n\}$$ 满足 $$4a_3 = 3a_2$$。
步骤：
1. 设首项为 $$a_1$$，公差为 $$d$$，则 $$a_2 = a_1 + d$$，$$a_3 = a_1 + 2d$$。
2. 代入条件：$$4(a_1 + 2d) = 3(a_1 + d)$$，化简得 $$a_1 + 5d = 0$$。
3. 通项公式：$$a_n = a_1 + (n-1)d$$。
4. 令 $$a_n = 0$$，解得 $$n = 6$$。
答案： A
3. 解析：
在等差数列 $$\{a_n\}$$ 中，$$a_1 > 0$$，且 $$5a_5 = 17a_9$$。
步骤：
1. 设首项为 $$a_1$$，公差为 $$d$$，则 $$a_5 = a_1 + 4d$$，$$a_9 = a_1 + 8d$$。
2. 代入条件：$$5(a_1 + 4d) = 17(a_1 + 8d)$$，化简得 $$12a_1 + 116d = 0$$，即 $$3a_1 + 29d = 0$$。
3. 通项公式：$$a_n = a_1 + (n-1)d$$。
4. 令 $$a_n = 0$$，解得 $$n = \frac{29}{3} + 1 \approx 10.67$$，故 $$S_n$$ 在 $$n = 10$$ 时最大。
答案： C
4. 解析：
在等差数列 $$\{a_n\}$$ 中，$$a_1 + 2a_2 + 3a_3 = 18$$。
步骤：
1. 设首项为 $$a_1$$，公差为 $$d$$，则 $$a_2 = a_1 + d$$，$$a_3 = a_1 + 2d$$。
2. 代入条件：$$a_1 + 2(a_1 + d) + 3(a_1 + 2d) = 18$$，化简得 $$6a_1 + 8d = 18$$，即 $$3a_1 + 4d = 9$$。
3. 求 $$2a_1 + a_5$$：$$a_5 = a_1 + 4d$$，故 $$2a_1 + a_5 = 3a_1 + 4d = 9$$。
答案： A
5. 解析：
塔共 $$9$$ 层，灯数总和为 $$126$$，且相邻两层灯数差为 $$n$$（常数），底层灯数是顶层的 $$13$$ 倍。
步骤：
1. 设顶层灯数为 $$a$$，则底层灯数为 $$13a$$。
2. 灯数为等差数列，总和 $$S_9 = \frac{9}{2}(a + 13a) = 126$$，解得 $$a = 2$$。
3. 底层灯数：$$13a = 26$$。
答案： C
6. 解析：
等差数列 $$\{a_n\}$$ 公差为 $$4$$，且 $$a_2, a_3, a_6$$ 成等比数列。
步骤：
1. 设首项为 $$a_1$$，则 $$a_2 = a_1 + 4$$，$$a_3 = a_1 + 8$$，$$a_6 = a_1 + 20$$。
2. 等比数列性质：$$(a_3)^2 = a_2 \cdot a_6$$，即 $$(a_1 + 8)^2 = (a_1 + 4)(a_1 + 20)$$。
3. 化简得 $$a_1 = -2$$。
4. 求 $$a_{10}$$：$$a_{10} = a_1 + 36 = 34$$。
答案： B
7. 解析：
在等差数列 $$\{a_n\}$$ 中，$$a_2 = 1$$，$$a_8 = 13$$。
步骤：
1. 设首项为 $$a_1$$，公差为 $$d$$，则 $$a_2 = a_1 + d = 1$$，$$a_8 = a_1 + 7d = 13$$。
2. 联立解得 $$d = 2$$。
答案： B
8. 解析：
等比数列 $$\{a_n\}$$ 中，公比 $$q$$，$$a_3 + a_5 = 10$$，$$a_2 \cdot a_6 = 16$$，且 $$b_n = \log_2 a_n$$。
步骤：
1. 由 $$a_2 \cdot a_6 = a_3 \cdot a_5 = 16$$，结合 $$a_3 + a_5 = 10$$，解得 $$a_3 = 2$$，$$a_5 = 8$$ 或反之。
2. 公比 $$q$$：$$a_5 = a_3 q^2$$，得 $$q = 2$$ 或 $$q = \frac{1}{2}$$。
3. 若 $$q = 2$$，则 $$a_n = 2^{n-2}$$，$$b_n = n - 2$$。
4. 计算 $$\frac{S_n}{n} = \frac{n-3}{2}$$，其最大值在 $$n = 9$$ 或 $$10$$ 时取得。
答案： C
9. 解析：
数列 $$\{a_n\}$$ 满足 $$a_{n+1} - a_n = 2$$，且 $$S_{10} = 50$$。
步骤：
1. 由递推式知 $$\{a_n\}$$ 为等差数列，公差 $$d = 2$$。
2. 利用 $$S_{10} = 50$$：$$\frac{10}{2}(2a_1 + 18) = 50$$，解得 $$a_1 = -4$$。
3. 通项公式：$$a_n = -4 + (n-1) \cdot 2 = 2n - 6$$。
4. 求 $$\{a_n + a_{n+1}\}$$ 的前 $$10$$ 项和：$$a_n + a_{n+1} = 4n - 10$$，和为 $$\sum_{k=1}^{10} (4k - 10) = 120$$。
答案： C
10. 解析：
题目不完整，无法解析。