正确率60.0%在小于$${{1}{0}{0}}$$的自然数中,所有被$${{7}}$$除余$${{2}}$$的数之和为()
B
A.$${{7}{6}{5}}$$
B.$${{6}{6}{5}}$$
C.$${{7}{6}{3}}$$
D.$${{6}{6}{3}}$$
2、['等差数列的通项公式', '一元二次不等式的解法', '等差数列的前n项和的性质']正确率60.0%已知等差数列$${{\{}{{a}_{n}}{\}}}$$的前项和为$${{S}_{n}}$$,若$$a_{1}=1, ~ S_{5}=2 5$$,则满足$$S_{n} < 1 0 a_{n}-9$$的$${{n}}$$的最大值为()
C
A.$${{1}{6}}$$
B.$${{1}{7}}$$
C.$${{1}{8}}$$
D.$${{1}{9}}$$
3、['等差中项', '等差数列的前n项和的性质', '等差数列的前n项和的应用']正确率40.0%已知等差数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和为$$S_{n}, \, \, a_{4}+a_{8}=a_{6}+7$$,则$$S_{1 1}=( \textsubscript{\Lambda} )$$
A
A.$${{7}{7}}$$
B.$${{8}{8}}$$
C.$${{1}{5}{4}}$$
D.$${{1}{7}{6}}$$
4、['等差数列的前n项和的性质', '等差数列的性质', '等差数列的前n项和的应用']正确率60.0%已知等差数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和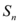 满足$${{S}_{5}{<}{{S}_{6}}}$$
满足$${{S}_{5}{<}{{S}_{6}}}$$
D
A.$${{S}_{6}}$$和$${{S}_{7}}$$均为$${{S}_{n}}$$的最大值.
B.$${{a}_{7}{=}{0}}$$;
C.公差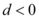 ;
;
D.$${{S}_{9}{>}{{S}_{5}}}$$;
5、['等差数列的前n项和的性质', '等差数列的性质', '等差数列的前n项和的应用']正确率60.0%在等差数列$${{\{}{{a}_{n}}{\}}}$$中,$${{S}_{n}}$$为其前$${{n}}$$项和,$$S_{9}=1 8, S_{n}=2 4 0, a_{n-4}=3 0$$,则$${{n}}$$的值为$${{(}{)}}$$
B
A.$${{1}{4}}$$
B.$${{1}{5}}$$
C.$${{1}{6}}$$
D.$${{1}{7}}$$
6、['等差数列的前n项和的性质', '等差数列的性质', '等差数列的前n项和的应用']正确率19.999999999999996%数列$$\{a_{n} \} \smallsetminus\{b_{n} \}$$均为等差数列,且前$${{n}}$$项和分别为$${{S}_{n}}$$和$${{T}_{n}}$$,若$$\frac{S_{n}} {T_{n}}=\frac{3 n+2} {n+1},$$则$$\frac{a_{5}} {b_{4}}=($$)
C
A.$$\frac{2 9} {1 0}$$
B.$$\frac{2 3} {8}$$
C.$$\frac{2 9} {8}$$
D.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
7、['等差数列的前n项和的性质', '等差数列的性质']正确率60.0%设$${{S}_{n}}$$是等差数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和,对$${{n}{∈}{N}{∗}}$$且$${{n}{>}{4}}$$时有$$S_{8}=2 0, \ S_{2 n-1}-S_{2 n-9}=1 1 6$$,则$${{a}_{n}{=}{(}}$$)
B
A.$${{6}}$$
B.$$\frac{1 7} {2}$$
C.$${{3}{9}}$$
D.$${{7}{8}}$$
8、['函数奇、偶性的证明', '函数单调性的判断', '等差数列的前n项和的性质']正确率19.999999999999996%设等差数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和为$${{S}_{n}}$$,且$$( a_{1}-3 )^{3}+3 ( a_{1}-3 )=-3, ~ ( a_{1 2}-3 )^{3}+3 ( a_{1 2}-3 )=3$$,则下列结论正确的是$${{(}{)}}$$
D
A.$$a_{1} > a_{1 2} \,, \, \, S_{1 2}=-3 6$$
B.$$a_{1} < a_{1 2}, \, \, \, S_{1 2}=-3 6$$
C.$$a_{1} > a_{1 2}, \, \, \, S_{1 2}=3 6$$
D.$$a_{1} < a_{1 2}, \, \, \, S_{1 2}=3 6$$
9、['等差数列的通项公式', '等比中项', '等差数列的前n项和的性质']正确率60.0%已知等差数列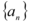 的公差不为零,
的公差不为零,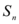 为其前$${{n}}$$
为其前$${{n}}$$
D
A.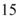
B.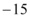
C.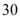
D.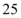
正确率60.0%北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层,上层中心有一块圆形石板(称为天心石$${{)}}$$,环绕天心石砌$${{9}}$$块扇面形石板构成第一环,向外每环依次增加$${{9}}$$块,下一层的第一环比上一层的最后一环多$${{9}}$$块,向外每环依次也增加$${{9}}$$块,已知每层环数相同,且下层比中层多$${{7}{2}{9}}$$块,则三层共有扇面形石板(不含天心石$${{)}}$$()
C
A.$${{3}{{6}{9}{9}}}$$块
B.$${{3}{{4}{7}{4}}}$$块
C.$${{3}{{4}{0}{2}}}$$块
D.$${{3}{{3}{3}{9}}}$$块
1. 解析:
2. 解析:
3. 解析:
4. 解析:
5. 解析:
6. 解析:
7. 解析:
8. 解析:
9. 解析:
10. 解析:
.jpg)