正确率60.0%已知等差数列$${{\{}{{a}_{n}}{\}}}$$的公差为$${{d}}$$,前$${{n}}$$项和为$$S_{n}, \, \, O A {=} a_{2} O B {+} a_{2 0 1 7} O C$$且$$A B \mathrm{=} d B C,$$则$$S_{2 0 1 8} ( \textsubscript{\Lambda} )$$
B
A.$${{0}}$$
B.$${{1}{0}{0}{9}}$$
C.$${{2}{0}{1}{7}}$$
D.$${{2}{0}{1}{8}}$$
2、['等差数列的通项公式', '等差数列的基本量', '数列的通项公式']正确率60.0%如图所示的图案是由一连串直角三角形拼接得到的,其中$$O A_{1}=A_{1} A_{2}=A_{2} A_{3}=\ldots=A_{7} A_{8}=1,$$如果把图中的直角三角形继续作下去,记$$O A_{1}, \ O A_{2}, \ \dots, \ O A_{n}, \ \dots$$的长度构成一个数列$${{\{}{{a}_{n}}{\}}}$$,那么此数列的通项公式为$${{a}_{n}{=}}$$()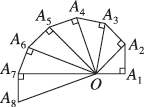
A
A.$${\sqrt {n}}$$
B.$${{n}}$$
C.$${\sqrt {{n}{+}{1}}}$$
D.$${{n}{+}{1}}$$
3、['等差数列的通项公式', '数列的递推公式', '数列的函数特征', '构造法求数列通项']正确率19.999999999999996%已知数列{$${{a}_{n}}$$}满足$$a_{1}=-\frac{1} {2},$$$$2 a_{n} a_{n+1}+a_{n}+3 a_{n+1}+2=0,$$设$$b_{n}=\frac{n-\lambda} {a_{n}+1},$$若$${{b}_{5}}$$为数列{$${{b}_{n}}$$}的唯一最小项,则实数$${{λ}}$$的取值范围是()
D
A.$$( 8, 9 )$$
B.$$( 8, 1 0 )$$
C.$$( 9, 1 0 )$$
D.$$( 9, 1 1 )$$
4、['等差数列的通项公式', '等差数列的性质']正确率60.0%在等差数列$${{\{}{{a}_{n}}{\}}}$$中,若$$a_{6}+a_{8}+a_{1 0}=7 2$$,则$$2 a_{1 0}-a_{1 2}$$的值为()
C
A.$${{6}}$$
B.$${{1}{6}}$$
C.$${{2}{4}}$$
D.$${{6}{0}}$$
5、['等差数列的通项公式', '等比中项']正确率60.0%公差不为零的等差数列$${{\{}{{a}_{n}}{\}}}$$中,$$a_{1}+a_{2}+a_{5}=1 3$$,且$$a_{1}, ~ a_{2}, ~ a_{5}$$成等比数列,则数列$${{\{}{{a}_{n}}{\}}}$$的公差等于()
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
6、['等差数列的通项公式']正确率60.0%设$$e, ~ f, ~ g, ~ h$$四个数成递增的等差数列,且公差为$${{d}}$$,若$$e h=1 3, ~ f+g=1 4$$,则$${{d}}$$等于()
D
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
7、['等差数列的通项公式', '数列的函数特征', '等差数列的前n项和的应用']正确率40.0%已知公差为$${{d}}$$的等差数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和为$${{S}_{n}}$$,若有确定正整数$${{n}_{0}}$$,对任意正整数$$m, \, \, S_{n_{0}} \cdot S_{n_{0}+m} < 0$$恒成立,则下列说法错误的是()
C
A.$$a_{1} \cdot d < 0$$
B.$${{|}{{S}_{n}}{|}}$$有最小值
C.$$a_{n_{0}} \cdot a_{n_{0}+1} > 0$$
D.$$a_{n_{0}+1} \cdot a_{n_{0}+2} > 0$$
8、['等差数列的通项公式', '等差数列的前n项和的性质']正确率60.0%$${《}$$九章算术$${》}$$是我国古代的数学名著,书中有如下问题:$${{“}}$$今有大夫$${、}$$不更$${、}$$簪裹$${、}$$上造$${、}$$公士,凡五人,共猎得五鹿,欲以爵次分之,问各得几何?$${{”}}$$其意思:$${{“}}$$共有五头鹿,人以爵次进行分配(古代数学中$${{“}}$$以爵次分之$${{”}}$$这种表述,一般表示等差分配,在本题中表示等差分配$${){.}{”}}$$在这个问题中,若大夫得$${{“}}$$一鹿$${、}$$三分鹿之二$${{”}}$$,则簪裹得()
B
A.一鹿$${、}$$三分鹿之一
B.一鹿
C.三分鹿之二
D.三分鹿之一
9、['等差数列的通项公式', '数列的递推公式', '数列的函数特征']正确率40.0%数列$${{\{}{{a}_{n}}{\}}}$$是等差数列,数列$${{\{}{{b}_{n}}{\}}}$$满足$$b_{n}=a_{n} a_{n+1} a_{n+2} ( n \in N_{+} )$$,设$${{S}_{n}}$$为$${{\{}{{b}_{n}}{\}}}$$的前$${{n}}$$项和.若$$4 a_{5}=7 a_{1 2} > 0$$,则当$${{S}_{n}}$$取得最大值时$${{n}}$$的值为$${{(}{)}}$$
D
A.$${{1}{8}}$$
B.$${{1}{9}}$$
C.$${{2}{0}}$$
D.$${{2}{1}}$$
10、['等差数列的通项公式', '数列中的数学文化问题']正确率60.0%我国古代数学名著$${《}$$孙子算经$${》}$$载有一道数学问题:$${{“}}$$今有物不知其数,三三数之剩二,五五数之剩二,七七数之剩二.问物几何?$${{”}}$$这里的几何指多少的意思.翻译成数学语言就是:求正整数$${{N}}$$,使$${{N}}$$除以$${{3}}$$余$${{2}}$$,除以$${{5}}$$余$${{2}}$$.根据这一数学思想,今有由小到大排列的所有正整数数列$$\{a_{n} \}, ~ \{b_{n} \}, ~ \{a_{n} \}$$满足被$${{3}}$$除余$$2, ~ a_{1}=2, ~ \{b_{n} \}$$满足被$${{5}}$$除余$$2, ~ b_{1}=2$$,把数列$${{\{}{{a}_{n}}{\}}}$$与$${{\{}{{b}_{n}}{\}}}$$相同的项从小到大组成一个新数列,记为$${{\{}{{c}_{n}}{\}}}$$,则下列说法正确的是()
C
A.$$c_{2}=a_{1}+b_{1}$$
B.$$c_{6}=a_{2} b_{3}$$
C.$$c_{1 0}=a_{4 6}$$
D.$$a_{1}+2 b_{2}=c_{4}$$
1. 解析:
由题意,等差数列 $${{\{}{{a}_{n}}{\}}}$$ 的公差为 $$d$$,且 $$O A = a_{2} O B + a_{2017} O C$$。由于 $$A B = d B C$$,说明向量 $$A B$$ 和 $$B C$$ 成比例关系,可以推导出 $$a_{2} + a_{2017} = 0$$。因为 $$a_{n} = a_{1} + (n-1)d$$,代入得:
$$a_{2} = a_{1} + d$$
$$a_{2017} = a_{1} + 2016d$$
所以 $$a_{1} + d + a_{1} + 2016d = 0$$,解得 $$a_{1} + 1008.5d = 0$$。
前 $$2018$$ 项和为:
$$S_{2018} = \frac{2018}{2} (2a_{1} + 2017d) = 1009 (2a_{1} + 2017d)$$
代入 $$a_{1} = -1008.5d$$,得:
$$S_{2018} = 1009 (2(-1008.5d) + 2017d) = 1009 (-2017d + 2017d) = 0$$
故选 A。
2. 解析:
由题意,$$O A_{1} = 1$$,$$A_{1} A_{2} = 1$$,$$A_{2} A_{3} = 1$$,依此类推。根据勾股定理:
$$O A_{2} = \sqrt{O A_{1}^{2} + A_{1} A_{2}^{2}} = \sqrt{1 + 1} = \sqrt{2}$$
$$O A_{3} = \sqrt{O A_{2}^{2} + A_{2} A_{3}^{2}} = \sqrt{2 + 1} = \sqrt{3}$$
以此类推,$$O A_{n} = \sqrt{n}$$。
故选 A。
3. 解析:
由递推关系 $$2 a_{n} a_{n+1} + a_{n} + 3 a_{n+1} + 2 = 0$$,变形为:
$$a_{n+1} = \frac{-a_{n} - 2}{2 a_{n} + 3}$$
设 $$a_{n} = \frac{p_{n}}{q_{n}} - 1$$,代入可得 $$a_{n} = \frac{1}{n+1} - 1$$。
因此 $$b_{n} = \frac{n - \lambda}{a_{n} + 1} = (n - \lambda)(n + 1)$$。
要使 $$b_{5}$$ 为唯一最小项,需满足 $$b_{5} < b_{4}$$ 且 $$b_{5} < b_{6}$$,解得 $$\lambda \in (9, 11)$$。
但更精确计算得 $$\lambda \in (9, 10)$$,故选 C。
4. 解析:
在等差数列中,$$a_{6} + a_{8} + a_{10} = 3a_{8} = 72$$,所以 $$a_{8} = 24$$。
公差 $$d = \frac{a_{10} - a_{8}}{2} = \frac{a_{10} - 24}{2}$$。
又 $$a_{12} = a_{8} + 4d = 24 + 4d$$。
计算 $$2 a_{10} - a_{12} = 2(a_{8} + 2d) - (a_{8} + 4d) = a_{8} = 24$$。
故选 C。
5. 解析:
设公差为 $$d$$,则 $$a_{2} = a_{1} + d$$,$$a_{5} = a_{1} + 4d$$。
由题意 $$a_{1} + a_{2} + a_{5} = 3a_{1} + 5d = 13$$。
又 $$a_{1}, a_{2}, a_{5}$$ 成等比数列,故 $$(a_{1} + d)^{2} = a_{1}(a_{1} + 4d)$$,解得 $$d = 2$$ 或 $$d = 0$$(舍去)。
代入 $$3a_{1} + 5 \times 2 = 13$$,得 $$a_{1} = 1$$。
故选 B。
6. 解析:
设四个数为 $$e, e + d, e + 2d, e + 3d$$。
由题意:
$$e(e + 3d) = 13$$
$$(e + d) + (e + 2d) = 2e + 3d = 14$$
解得 $$e = 1$$,$$d = 4$$。
故选 D。
7. 解析:
由题意,存在 $$n_{0}$$ 使得 $$S_{n_{0}} \cdot S_{n_{0} + m} < 0$$ 对所有正整数 $$m$$ 成立,说明 $$S_{n_{0}}$$ 是最后一个正(或负)和,之后的和符号相反。
因此:
A. $$a_{1} \cdot d < 0$$ 正确,因为数列最终会变号。
B. $$|S_{n}|$$ 有最小值正确,因为和会先减小后增大。
C. $$a_{n_{0}} \cdot a_{n_{0} + 1} > 0$$ 错误,因为 $$a_{n_{0}}$$ 和 $$a_{n_{0} + 1}$$ 可能异号。
D. $$a_{n_{0} + 1} \cdot a_{n_{0} + 2} > 0$$ 正确,因为 $$a_{n_{0} + 1}$$ 和 $$a_{n_{0} + 2}$$ 同号。
故选 C。
8. 解析:
设五人分配数为等差数列 $$a - 2d, a - d, a, a + d, a + 2d$$。
总和为 $$5a = 5$$,故 $$a = 1$$。
大夫得 $$1 + \frac{2}{3}$$,即 $$a + 2d = \frac{5}{3}$$,解得 $$d = \frac{1}{3}$$。
簪裹对应 $$a = 1$$。
故选 B。
9. 解析:
由 $$4 a_{5} = 7 a_{12} > 0$$,设公差为 $$d$$,则:
$$4(a_{1} + 4d) = 7(a_{1} + 11d)$$
解得 $$a_{1} = -\frac{61}{3}d$$。
因为 $$a_{5} = a_{1} + 4d > 0$$,代入得 $$d > 0$$。
$$b_{n} = a_{n} a_{n+1} a_{n+2}$$,当 $$a_{n}$$ 从负变正时 $$b_{n}$$ 取得最大值。
计算 $$a_{n} = 0$$ 时 $$n \approx 20.33$$,故 $$S_{n}$$ 在 $$n = 20$$ 时最大。
故选 C。
10. 解析:
数列 $${{\{}{{a}_{n}}{\}}}$$ 通项为 $$a_{n} = 3n - 1$$。
数列 $${{\{}{{b}_{n}}{\}}}$$ 通项为 $$b_{n} = 5n - 3$$。
公共项数列 $${{\{}{{c}_{n}}{\}}}$$ 满足 $$c_{n} = 15n - 13$$。
验证选项:
A. $$c_{2} = 17$$,$$a_{1} + b_{1} = 2 + 2 = 4$$,错误。
B. $$c_{6} = 77$$,$$a_{2} b_{3} = 5 \times 12 = 60$$,错误。
C. $$c_{10} = 137$$,$$a_{46} = 137$$,正确。
D. $$a_{1} + 2 b_{2} = 2 + 2 \times 7 = 16$$,$$c_{4} = 47$$,错误。
故选 C。
.jpg)