.jpg)
正确率60.0%设数列$${{\{}}$$ $${{a}_{n}}$$$${{\}}}$$的通项公式为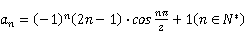
，其前 $${{n}}$$项和为$${{S}}$$ $${_{n}}$$，则$$S_{1 2 0}=$$
D
A.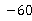
B.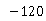
C.$${{1}{8}{0}}$$
D.$${{2}{4}{0}}$$
2、['数列的函数特征'， '单调性的定义与证明'， '数列的通项公式']正确率40.0%已知$$f ( x )=\left\{\begin{array} {l l} {( 2 a-1 ) x+4， x \leq1} \\ {a^{x}， x > 1} \\ \end{array} \right.$$定义域为$${{R}}$$，数列$$\{a_{n} \} ( n \in N^{*} )， \， \， a_{n}=f ( n )$$是递增数列，则$${{a}}$$的取值范围是（）
D
A.$$( 1， ~+\infty)$$
B.$$( \frac{1} {2}， ~+\infty)$$
C.$$( 1， \ 3 )$$
D.$$( \mathbf{3}， \mathbf{\Lambda}+\infty)$$
3、['数列的递推公式'， '累乘法求数列通项'， '常见函数的零点'， '数列的通项公式']正确率40.0%首项为$${{1}}$$的 正项数列$$\{a_{n} \}， ~ a_{n+1}$$是函数$$f ( x )=( n+1 ) x^{2}+a_{n} ( x-n a_{n} ) ( n \in N^{*} )$$的零点，则$$\operatorname{l g} a_{1 0 0}$$等于
B
A.$${{1}}$$
B.$${{−}{2}}$$
C.$${{l}{g}{{1}{0}{1}}}$$
D.$${{2}}$$
4、['数列的递推公式'， '数列的通项公式']正确率40.0%数列$${{\{}{{a}_{n}}{\}}}$$中，$$a_{1}=\frac{1} {2}$$，前$${{n}}$$项和$$S_{n}=n^{2} a_{n}$$，求$${{a}_{n}{=}}$$（）
B
A.$$\frac{1} {n ( n-1 )}$$
B.$$\frac{1} {n ( n+1 )}$$
C.$$\frac2 {( n+1 )^{2}}$$
D.$$\frac{3} {( n+1 ) ( n+2 )}$$
5、['数列的通项公式']正确率60.0%数列
的第$${{6}}$$项是（）
A
A.$${{4}{2}}$$
B.$${{5}{6}}$$
C.$${{9}{0}}$$
D.$${{7}{2}}$$
6、['数列的通项公式']正确率60.0%已知数列｛$${{a}_{n}}$$｝的前$${{4}}$$项分别为$$- \frac{1} {2}， ~ \frac{3} {4}， ~-\frac{5} {8}， ~ \frac{7} {1 6}，$$则数列｛$${{a}_{n}}$$｝的通项公式是（）
B
A.$$a_{n}=\frac{2 n-1} {2^{n}}$$
B.$$a_{n}=\frac{(-1 )^{n} \cdot( 2 n-1 )} {2^{n}}$$
C.$$a_{n}=\frac{2 n+1} {2^{n}}$$
D.$$a_{n}=\frac{(-1 )^{n} \cdot( 2 n+1 )} {2^{n}}$$
7、['数列的定义与概念'， '数列的通项公式']正确率60.0%已知一个数列的前四项为$$\frac{1} {2^{2}}，-\frac{3} {4^{2}}， \frac{5} {8^{2}}，-\frac{7} {1 6^{2}}，$$则它的一个通项公式为（）
D
A.$$\left(-1 \right)^{n} \frac{2 n-1} {\left( 2 n \right)^{2}}$$
B.$$(-1 )^{n-1} \frac{2 n-1} {\left( 2 n \right)^{2}}$$
C.$$(-1 )^{n} \， \frac{2 n-1} {2^{2 n}}$$
D.$$(-1 )^{n-1} \frac{2 n-1} {2^{2 n}}$$
8、['数列的递推公式'， '裂项相消法求和'， '数列的通项公式']正确率40.0%数列$${{\{}{{a}_{n}}{\}}}$$中，$${{a}_{1}{=}{1}}$$，对任意$${{n}{∈}{{N}^{∗}}}$$，有$$a_{n+1}=1+n+a_{n}$$，令$$b_{i}=\frac{1} {a_{i}}， \quad( \， i \in N^{*} \， )$$，则$$b_{1}+b_{2}+\ldots+b_{2 0 1 8}=\alpha$$）
D
A.$$\frac{2 0 1 7} {1 0 0 9}$$
B.$$\frac{2 0 1 7} {2 0 1 8}$$
C.$$\frac{2 0 1 8} {2 0 1 9}$$
D.$$\frac{4 0 3 6} {2 0 1 9}$$
9、['数列的通项公式']正确率60.0%已知数列$${{\{}{{a}_{n}}{\}}}$$的通项公式是$$a_{n}=2-3 n$$，则该数列的第五项是（）
A
A.$${{−}{{1}{3}}}$$
B.$${{1}{3}}$$
C.$${{−}{{1}{1}}}$$
D.$${{−}{{1}{6}}}$$
10、['数列的通项公式']正确率60.0%数列$$1， ~-3， ~ 5， ~-7， ~ \ldots$$的一个通项公式为$${{(}{)}}$$
B
A.$$a_{n}=2 n-1$$
B.$$a_{n}=(-1 )^{n+1} ( 2 n-1 )$$
C.$$a_{n}=(-1 )^{n} ( 2 n-1 )$$
D.$$a_{n}=(-1 )^{n} ( 2 n+1 )$$
1. 解析：
数列通项公式为 $$a_n = \frac{1}{\sqrt{n} + \sqrt{n+1}}$$，可通过有理化化简：
$$a_n = \sqrt{n+1} - \sqrt{n}$$
前 $$n$$ 项和 $$S_n$$ 为：
$$S_n = (\sqrt{2} - \sqrt{1}) + (\sqrt{3} - \sqrt{2}) + \cdots + (\sqrt{n+1} - \sqrt{n}) = \sqrt{n+1} - 1$$
因此，$$S_{120} = \sqrt{121} - 1 = 11 - 1 = 10$$，对应选项 A。
2. 解析：
分段函数 $$f(x)$$ 在 $$x \leq 1$$ 时为一次函数，$$x > 1$$ 时为指数函数。数列 $$\{a_n\}$$ 递增需满足：
(1) $$2a - 1 > 0$$（一次函数斜率大于 0）；
(2) $$a > 1$$（指数函数底数大于 1）；
(3) 分段点 $$x=1$$ 处函数值关系：$$(2a-1) \cdot 1 + 4 \leq a^1$$，即 $$2a + 3 \leq a$$，矛盾。需调整为 $$f(1) < f(2)$$：
$$2a + 3 < a^2$$，解得 $$a > 3$$。
综上，$$a$$ 的取值范围是 $$(3, +\infty)$$，对应选项 D。
3. 解析：
函数 $$f(x) = (n+1)x^2 + a_n(x - n a_n)$$ 的零点为 $$a_{n+1}$$，代入得：
$$(n+1)a_{n+1}^2 + a_n a_{n+1} - n a_n^2 = 0$$
因 $$a_n > 0$$，解得 $$a_{n+1} = \frac{n}{n+1} a_n$$。
递推得通项：
$$a_n = \frac{1}{n}$$，故 $$a_{100} = \frac{1}{100}$$，$$\lg a_{100} = \lg \frac{1}{100} = -2$$，对应选项 B。
4. 解析：
已知 $$S_n = n^2 a_n$$，且 $$S_n = S_{n-1} + a_n$$，代入得：
$$n^2 a_n = (n-1)^2 a_{n-1} + a_n$$
整理得：
$$a_n = \frac{(n-1)^2}{n^2 - 1} a_{n-1} = \frac{n-1}{n+1} a_{n-1}$$
递推得通项：
$$a_n = \frac{1}{n(n+1)}$$，对应选项 B。
5. 解析：
数列通项为 $$a_n = n^2 + n$$，第六项为：
$$a_6 = 6^2 + 6 = 42$$，对应选项 A。
6. 解析：
观察前四项符号交替，分子为奇数 $$2n-1$$，分母为 $$2^n$$，故通项为：
$$a_n = \frac{(-1)^n (2n-1)}{2^n}$$，对应选项 B。
7. 解析：
观察前四项符号交替，分子为奇数 $$2n-1$$，分母为 $$(2^n)^2 = 2^{2n}$$，故通项为：
$$a_n = (-1)^n \frac{2n-1}{2^{2n}}$$，对应选项 C。
8. 解析：
递推关系 $$a_{n+1} = a_n + n + 1$$，累加得：
$$a_n = 1 + \sum_{k=1}^{n-1} (k + 1) = \frac{n(n+1)}{2}$$
因此 $$b_i = \frac{2}{i(i+1)} = 2\left(\frac{1}{i} - \frac{1}{i+1}\right)$$，求和得：
$$b_1 + \cdots + b_{2018} = 2\left(1 - \frac{1}{2019}\right) = \frac{4036}{2019}$$，对应选项 D。
9. 解析：
通项公式 $$a_n = 2 - 3n$$，第五项为：
$$a_5 = 2 - 3 \times 5 = -13$$，对应选项 A。
10. 解析：
数列符号交替，奇数项为正，通项为：
$$a_n = (-1)^{n+1} (2n - 1)$$，对应选项 B。