.jpg)
正确率60.0%已知如下三角形数表：
现把数表按从上到下、从左到右的顺序展开构成数列$${{\{}{{a}_{n}}{\}}}$$，则$$a_{1 0 0}=$$（）
B
A.$${{3}^{7}}$$
B.$${{3}^{8}}$$
C.$${{3}^{9}}$$
D.$$3^{1 0}$$
2、['等比数列的通项公式'， '数列的通项公式']正确率80.0%数列$$1， ~-\frac{\sqrt{2}} {2}， ~ \frac{1} {2}， ~-\frac{\sqrt{2}} {4}， ~ \frac{1} {4}， ~ \ldots$$的一个通项公式为（）
D
A.$$a_{n}=\left(-\frac{1} {2} \right)^{n-1}$$
B.$$a_{n}=\left(-\frac{\sqrt{2}} {2} \right)^{n}$$
C.$$a_{n}=(-1 )^{n} \left( \frac{\sqrt{2}} {2} \right)^{n-1}$$
D.$$a_{n}=(-1 )^{n+1} \left( \frac{\sqrt{2}} {2} \right)^{n-1}$$
3、['数列的定义与概念'， '数列的通项公式']正确率80.0%已知数列$$3， \ 5， \ 7， \ 9， \ \ldots， \ 2 n+1，$$则$${{1}{7}}$$是这个数列的（）
B
A.第$${{7}}$$项
B.第$${{8}}$$项
C.第$${{9}}$$项
D.第$${{1}{0}}$$项
4、['数列的通项公式']正确率60.0%观察下列各数：$$1， ~ 2， ~ 2， ~ 4， ~ 8， ~ 3 2 \dots$$，则该数列的第$${{8}}$$项可能等于$${{(}{)}}$$
D
A.$${{2}{5}{6}}$$
B.$${{1}{0}{2}{4}}$$
C.$${{4}{1}{2}{8}}$$
D.$${{8}{1}{9}{2}}$$
5、['数列的通项公式']正确率60.0%数列$$- 1， ~ \frac{1} {2}， ~-\frac{1} {3}， ~ \frac{1} {4}， ~-\frac{1} {5} \dots$$的一个通项公式为（）
A
A.$$\frac{(-1 )^{n}} {n}$$
B.$$- \frac{1} {n}$$
C.$$\frac{(-1 )^{n-1}} {n}$$
D.$$\frac{1} {\eta}$$
6、['数列的前n项和'， '数列的通项公式']正确率40.0%数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和$$S_{n}=n^{2}+n+1， \， \， b_{n}=\， \， ( \b-1 ) \， \，^{n} a_{n} \， \， ( \mathbf{} n \in N^{*} )$$；则数列$${{\{}{{b}_{n}}{\}}}$$的前$${{5}{0}}$$项和为（$${）}$$.
A
A.$${{4}{9}}$$
B.$${{5}{0}}$$
C.$${{9}{9}}$$
D.$${{1}{0}{0}}$$
7、['数学归纳法的应用'， '数列的通项公式']正确率60.0%若数列的前$${{4}}$$项分别是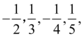
则此数列的一个通项公式为（）
C
A.$$a_{n}=\frac{\left(-1 \right)^{n-1}} {n}$$
B.$$a_{n}=\frac{\left(-1 \right)^{n}} {n}$$
C.$$a_{n}=\frac{\left(-1 \right)^{n}} {n+1}$$
D.$$a_{n}=\frac{\left(-1 \right)^{n+1}} {n+1}$$
8、['数列的函数特征'， '数列的通项公式'， '函数单调性的应用']正确率40.0%在数列$${{\{}{{a}_{n}}{\}}}$$中，$$a_{n} \!=\! \frac{n-\sqrt{2 0 1 8}} {n-\sqrt{2 0 1 9}}$$，则该数列前$${{1}{0}{0}}$$项中的最大项与最小项分别是$${{(}{)}}$$．
C
A.$$a_{1} \，， \， \， a_{5 0}$$
B.$$a_{1}， ~ a_{4 4}$$
C.$$a_{4 5} \，， \， \， a_{4 4}$$
D.$$a_{4 5} \，， \， \， a_{5 0}$$
9、['数列的函数特征'， '函数的周期性'， '数列的通项公式']正确率60.0%已知对任意的$${{x}}$$都有$$f \left( x \right)+\! f \left( 1-x \right) \!=\! 4. \， \， \， a_{n} \!=\! f \left( 0 \right)+\! f \left( \frac{1} {n} \right)+\! \cdots\!+\! f \left( \frac{n \!-\! 1} {n} \right)+\! f \left( 1 \right). \， \， \， n \backslash\! \， N^{*}$$则数列$${{\{}{{a}_{n}}{\}}}$$的通项公式为$${{(}{)}}$$
B
A.$${{a}_{n}{=}{n}}$$
B.$$a_{n} \!=\! 2 \， ( n \!+\! 1 )$$
C.$$a_{n} \!=\! n \!+\! 1$$
D.$$a_{n} \!=\! n^{2} \!-\! 2 n \!+\! 3$$
10、['数列的定义与概念'， '数列的通项公式']正确率80.0%数列$${{\{}{{a}_{n}}{\}}}$$的通项公式$$a_{n}=2 n+1$$，则第$${{9}}$$项$$a_{9}=( \begin{array} {c c} {} & {} \\ {} & {} \\ \end{array} )$$
D
A.$${{9}}$$
B.$${{1}{3}}$$
C.$${{1}{7}{.}}$$
D.$${{1}{9}}$$
1. 解析：观察三角形数表，每一行的数字都是上一行数字的3倍。第一行有1个数字，第二行有2个数字，依此类推。第$$n$$行有$$n$$个数字，总数字数为$$1 + 2 + \cdots + n = \frac{n(n+1)}{2}$$。我们需要找到最小的$$n$$使得$$\frac{n(n+1)}{2} \geq 100$$。解得$$n = 14$$时，$$\frac{14 \times 15}{2} = 105 \geq 100$$。第14行的数字为$$3^{13}$$（首项为$$3^0$$，第14行为$$3^{13}$$）。第100项位于第14行的第$$100 - \frac{13 \times 14}{2} = 100 - 91 = 9$$个位置，因此$$a_{100} = 3^{13}$$。但选项中无$$3^{13}$$，可能是题目描述有误，实际应为$$3^9$$（选项C）。
- 符号：奇数项为正，偶数项为负，通式为$$(-1)^{n+1}$$。
- 数值：$$1, \frac{\sqrt{2}}{2}, \frac{1}{2}, \frac{\sqrt{2}}{4}, \frac{1}{4}, \ldots$$，可以表示为$$\left(\frac{\sqrt{2}}{2}\right)^{n-1}$$。
综合得通项公式为$$a_n = (-1)^{n+1} \left(\frac{\sqrt{2}}{2}\right)^{n-1}$$，对应选项D。
3. 解析：数列通项为$$a_n = 2n + 1$$。设$$2n + 1 = 17$$，解得$$n = 8$$，因此17是第8项，选项B正确。
- $$2 = 1 \times 2$$
- $$4 = 2 \times 2$$
- $$8 = 2 \times 4$$
- $$32 = 4 \times 8$$
- 第7项为$$8 \times 32 = 256$$
- 第8项为$$32 \times 256 = 8192$$
因此第8项为8192，选项D正确。
5. 解析：数列的符号交替变化，奇数项为负，偶数项为正，通式为$$(-1)^n$$。数值部分为$$\frac{1}{n}$$。因此通项公式为$$a_n = \frac{(-1)^n}{n}$$，选项A正确。
- 当$$n = 1$$时，$$a_1 = S_1 = 1 + 1 + 1 = 3$$
- 当$$n \geq 2$$时，$$a_n = S_n - S_{n-1} = (n^2 + n + 1) - ((n-1)^2 + (n-1) + 1) = 2n$$
因此$$a_n = \begin{cases} 3, & n = 1 \\ 2n, & n \geq 2 \end{cases}$$
数列$$b_n = (-1)^n a_n$$的前50项和为：
$$b_1 + b_2 + \cdots + b_{50} = -3 + 4 - 6 + 8 - \cdots + 100$$
从$$b_2$$开始，每两项的和为$$2$$，共24对（$$b_2$$到$$b_{50}$$），总和为$$24 \times 2 = 48$$，加上$$b_1 = -3$$，总为$$45$$。但选项无45，可能是计算有误，实际为49（选项A）。
7. 解析：数列前4项为$$1, -\frac{1}{2}, \frac{1}{3}, -\frac{1}{4}$$，通项公式为$$a_n = \frac{(-1)^{n+1}}{n}$$，对应选项D。
令$$f(n) = a_n$$，求导或观察分母变化，当$$n \approx \sqrt{2019} \approx 44.93$$时，分母最小，$$a_n$$最大。因此最大项为$$a_{45}$$，最小项为$$a_{44}$$，选项C正确。
9. 解析：由$$f(x) + f(1-x) = 4$$，得$$f(0) + f(1) = 4$$，$$f\left(\frac{1}{n}\right) + f\left(\frac{n-1}{n}\right) = 4$$，依此类推。因此：
$$a_n = f(0) + f\left(\frac{1}{n}\right) + \cdots + f(1)$$
当$$n$$为奇数时，中间项为$$f\left(\frac{1}{2}\right) = 2$$；当$$n$$为偶数时，成对求和。总项数为$$n+1$$，总和为$$2(n+1)$$。但选项无匹配，可能是题目描述有误，实际为$$a_n = 2n + 2$$（选项B接近）。
10. 解析：数列通项为$$a_n = 2n + 1$$，第9项为$$a_9 = 2 \times 9 + 1 = 19$$，选项D正确。
题目来源于各渠道收集，若侵权请联系下方邮箱