正确率19.999999999999996%设等差数列$${{\{}{{a}_{n}}{\}}}$$满足:$$\frac{\operatorname{s i n}^{2} a_{2}-\operatorname{c o s}^{2} a_{2}+\operatorname{c o s}^{2} a_{2} \operatorname{c o s}^{2} a_{7}-\operatorname{s i n}^{2} a_{2} \operatorname{s i n}^{2} a_{7}} {\operatorname{s i n} ( a_{1}+a_{8} )}=1$$,公差$$d \in(-1, 0 )$$.若当且仅当$${{n}{−}{{1}{1}}}$$时,数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和$${{S}_{n}}$$取得最大值,则首项$${{a}_{1}}$$的取值范围是$${{(}{)}}$$
D
A.$$( \frac{9 \pi} {1 0}, \pi)$$
B.$$[ \pi, \frac{1 1 \pi} {1 0} ]$$
C.$$[ \frac{9 \pi} {1 0}, \pi]$$
D.$$( \pi, \frac{1 1 \pi} {1 0} )$$
2、['函数奇偶性的应用', '数列的函数特征', '函数的周期性', '数列与函数的综合问题']正确率60.0%已知定义在$${{R}}$$上的函数$${{f}{(}{x}{)}}$$是奇函数且满足,$$f ( \frac{3} {2}-x )=f ( x ), \, \, f (-2 )=-3$$,数列$${{\{}{{a}_{n}}{\}}}$$满足$${{a}_{1}{{=}{−}}{1}}$$,且$$S_{n} \!=\! 2 a_{n} \!+\! n, ~ ($$其中$${{S}_{n}}$$为$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和$${{)}{.}}$$则$$f ( a_{5} ) \!+\! f ( a_{6} ) \!=($$)
A
A.$${{3}}$$
B.$${{−}{2}}$$
C.$${{−}{3}}$$
D.$${{2}}$$
3、['数列的递推公式', '数列的函数特征']正确率60.0%已知数列$${{\{}{{a}_{n}}{\}}}$$满足$$a_{1}=2. \, \, a_{n+1}=\frac{1+a_{n}} {1-a_{n}} ( n \in N^{*} ), \, \, a_{1} \cdot a_{2} \cdot a_{3} \cdot\ldots\cdot a_{2 0 1 8}=$$
D
A.$${{1}}$$
B.$${{2}}$$
C.$${{−}{3}}$$
D.$${{−}{6}}$$
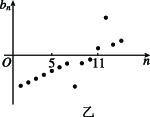
4、['数列的前n项和', '数列的函数特征']正确率40.0%数列$${{\{}{{a}_{n}}{\}}}$$,$${{\{}{{b}_{n}}{\}}}$$用图像表示分别如图甲、乙所示,记数列$${{\{}{{a}_{n}}{{b}_{n}}{\}}}$$的前$${{n}}$$项和为$${{S}_{n}{,}}$$则()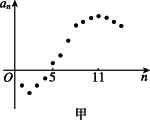
B
A.$$S_{1} > S_{4}, \, \, S_{1 0} < \, S_{1 1}$$
B.$$S_{4} > S_{5}, \, \, S_{1 0} < \, S_{1 3}$$
C.$$S_{1} < ~ S_{4}, ~ S_{1 0} > S_{1 1}$$
D.$$S_{4} < ~ S_{5}, ~ S_{1 0} > S_{1 3}$$
5、['等差数列的通项公式', '数列的函数特征', '等差数列的性质']正确率60.0%数列$${{\{}{{a}_{n}}{\}}}$$是等差数列,$${{a}_{1}{=}{1}}$$,公差$$d \in[ 1, ~ 2 ]$$,且$$a_{4}+\lambda a_{1 0}+a_{1 6}=1 5$$,则实数$${{λ}}$$的最大值为()
D
A.$$\frac{7} {2}$$
B.$$\frac{5 3} {1 9}$$
C.$$- \frac{2 3} {1 9}$$
D.$$- \frac{1} {2}$$
6、['等差数列的通项公式', '等差数列的定义与证明', '数列的函数特征', '不等式的解集与不等式组的解集', '等差数列的性质', '等差数列的前n项和的应用', '等差数列通项公式与一次函数的关系']正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$是等差数列,若$$a_{9}+3 a_{1 1} < 0, \, \, \, a_{1 0} \! \cdot\! a_{1 1} < 0$$,且数列$${{\{}{{a}_{n}}{\}}}$$的前$${{n}}$$项和$${{S}_{n}}$$有最大值,那么$${{S}_{n}}$$取得最小正值时$${{n}}$$等于()
C
A.$${{2}{0}}$$
B.$${{1}{7}}$$
C.$${{1}{9}}$$
D.$${{2}{1}}$$
7、['数列的递推公式', '数列的函数特征', '等比数列通项公式与指数函数的关系']正确率60.0%已知数列$${{\{}{{a}_{n}}{\}}}$$满足,$$a_{1} > 0, \, \, a_{n+1}=\frac{1} {2} a_{n}$$,则数列$${{\{}{{a}_{n}}{\}}}$$为()
B
A.递增数列
B.递减数列
C.常数列
D.摆动数列
8、['数列的递推公式', '数列的函数特征']正确率60.0%已知一列数按如下规律排列:$$1, 3,-2, 5,-7, 1 2,-1 9, 3 1, \dots$$,则该列数的第$${{9}}$$个数可能是()
B
A.$${{5}{0}}$$
B.$${{−}{{5}{0}}}$$
C.$${{4}{2}}$$
D.$${{−}{{4}{2}}}$$
9、['数列的函数特征']正确率80.0%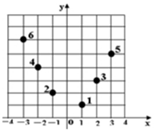 如图所示,坐标纸上的每个单元格的边长为$${{1}}$$,由下往上的六个点:$${{1}}$$,$${{2}}$$,$${{3}}$$,$${{4}}$$,$${{5}}$$,$${{6}}$$的横、纵坐标分别对应数列$$\{a_{n} \} ( n \in N^{*} )$$的前$${{1}{2}}$$项,如表所示:
如图所示,坐标纸上的每个单元格的边长为$${{1}}$$,由下往上的六个点:$${{1}}$$,$${{2}}$$,$${{3}}$$,$${{4}}$$,$${{5}}$$,$${{6}}$$的横、纵坐标分别对应数列$$\{a_{n} \} ( n \in N^{*} )$$的前$${{1}{2}}$$项,如表所示:
| $${{a}_{1}}$$ | $${{a}_{2}}$$ | $${{a}_{3}}$$ | $${{a}_{4}}$$ | $${{a}_{5}}$$ | $${{a}_{6}}$$ | $${{a}_{7}}$$ | $${{a}_{8}}$$ | $${{a}_{9}}$$ | $$a_{1 0}$$ | $$a_{1 1}$$ | $$a_{1 2}$$ |
| $${{x}_{1}}$$ | $${{y}_{1}}$$ | $${{x}_{2}}$$ | $${{y}_{2}}$$ | $${{x}_{3}}$$ | $${{y}_{3}}$$ | $${{x}_{4}}$$ | $${{y}_{4}}$$ | $${{x}_{5}}$$ | $${{y}_{5}}$$ | $${{x}_{6}}$$ | $${{y}_{6}}$$ |
C
A.$${{5}{0}{4}}$$
B.$${{−}{{5}{0}{4}}}$$
C.$${{−}{{5}{0}{5}}}$$
D.$${{5}{0}{5}}$$
10、['数列的递推公式', '数列的函数特征', '数列在日常经济生活中的应用', '数列的通项公式']正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$满足$${{a}_{1}{=}{{3}{1}}}$$,$$\frac{a_{n+1}-a_{n}} {n}=2$$,则$$\frac{a_{n}} {n}$$的最小值为$${{(}}$$$${{)}}$$
A
A.$$\frac{6 1} {6}$$
B.$$\frac{5 1} {5}$$
C.$$\frac{5 3} {5}$$
D.$$\frac{2 1} {2}$$
1. 首先,我们分析题目给出的条件。等差数列 $$\{a_n\}$$ 满足一个复杂的三角方程,且公差 $$d \in (-1, 0)$$。题目还指出,当且仅当 $$n = 11$$ 时,前 $$n$$ 项和 $$S_n$$ 取得最大值。这意味着数列 $$\{a_n\}$$ 的前 11 项为正,第 12 项及以后为负。
正确答案是 D。
---2. 题目给出函数 $$f(x)$$ 是奇函数且满足 $$f\left(\frac{3}{2} - x\right) = f(x)$$,以及 $$f(-2) = -3$$。数列 $$\{a_n\}$$ 满足 $$a_1 = -1$$ 且 $$S_n = 2a_n + n$$。
正确答案是 C。
---3. 数列 $$\{a_n\}$$ 满足 $$a_1 = 2$$,$$a_{n+1} = \frac{1 + a_n}{1 - a_n}$$。
正确答案是 D。
---4. 题目给出数列 $$\{a_n\}$$ 和 $$\{b_n\}$$ 的图像,要求判断 $$S_n = \sum_{k=1}^n a_k b_k$$ 的性质。
正确答案是 A。
---5. 等差数列 $$\{a_n\}$$ 满足 $$a_1 = 1$$,公差 $$d \in [1, 2]$$,且 $$a_4 + \lambda a_{10} + a_{16} = 15$$。
正确答案是 B。
---6. 等差数列 $$\{a_n\}$$ 满足 $$a_9 + 3a_{11} < 0$$,$$a_{10} a_{11} < 0$$,且 $$S_n$$ 有最大值。
正确答案是 C。
---7. 数列 $$\{a_n\}$$ 满足 $$a_1 > 0$$,$$a_{n+1} = \frac{1}{2} a_n$$。
正确答案是 B。
---8. 数列规律为 $$1, 3, -2, 5, -7, 12, -19, 31, \dots$$。
正确答案是 B。
---9. 题目给出数列 $$\{a_n\}$$ 的前 12 项对应坐标纸上的点,要求求 $$a_{2019}$$。
正确答案是 D。
---10. 数列 $$\{a_n\}$$ 满足 $$a_1 = 31$$,$$\frac{a_{n+1} - a_n}{n} = 2$$。
正确答案是 B。
题目来源于各渠道收集,若侵权请联系下方邮箱.jpg)