正确率60.0%已知数列$${{\{}{{a}_{n}}{\}}}$$,$${{\{}{{b}_{n}}{\}}}$$的部分图像如图所示,记数列$${{\{}{{a}_{n}{{b}_{n}}}{\}}}$$的前$${{n}}$$项和为$${{S}_{n}{,}}$$则()
B
A.$$S_{1} > S_{4}, \, \, S_{1 0} < S_{1 1}$$
B.$$S_{4} > S_{5}, \, \, S_{1 0} < S_{1 3}$$
C.$$S_{1} < S_{4}, \ S_{1 0} > S_{1 1}$$
D.$$S_{4} < S_{5}, \ S_{1 0} > S_{1 3}$$
2、['数列的定义与概念']正确率60.0%若把正整数按如图所示的规律排列,则从$${{2}{0}{1}{9}}$$到$${{2}{0}{2}{1}}$$的箭头方向依次为()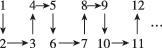
C
A.$${{↓}{→}}$$
B.$${{→}{↓}}$$
C.$${{↑}{→}}$$
D.$${{→}{↑}}$$
3、['数列的定义与概念', '数列的函数特征']正确率60.0%数列$${{\{}{{a}_{n}}{\}}}$$中,$$a_{n}=\frac{n-\sqrt{2 0 1 1}} {n-2 0 1 2}$$,则该数列前$${{1}{0}{0}}$$项中的最大项与最小项分别是$${{(}{)}}$$
C
A.$$a_{1}, a_{5 0}$$
B.$$a_{1}, a_{4 4}$$
C.$$a_{4 5}, a_{4 4}$$
D.$$a_{4 5}, a_{5 0}$$
4、['数列的定义与概念', '数列的函数特征', '数列的通项公式']正确率40.0%已知数列$${{\{}{{a}_{n}}{\}}}$$满足$$a_{n}=\frac{3} {3 n-1 6}$$,前$${{n}}$$项和为$${{S}_{n}}$$,则下列关于$${{a}_{n}{、}{{S}_{n}}}$$叙述正确的是$${{(}{)}}$$
B
A.$${{a}_{n}{,}{{S}_{n}}}$$都有最大值
B.$${{a}_{n}{,}{{S}_{n}}}$$都有最小值
C.$${{a}_{n}{,}{{S}_{n}}}$$都没有最大值
D.$${{a}_{n}{,}{{S}_{n}}}$$都没有最小值
5、['数列的定义与概念', '等差数列的定义与证明', '数列的通项公式']正确率60.0%已知数列$$3.$$那么$${{8}{1}}$$是它的第几项()
C
A.$${{1}{2}}$$
B.$${{1}{3}}$$
C.$${{1}{4}}$$
D.$${{1}{5}}$$
6、['数列的定义与概念', '数列的通项公式']正确率80.0%数列$$\frac1 3, \frac2 5, \frac3 7, \frac4 9, \dots$$的通项公式$${{a}_{n}}$$是$${{(}{)}}$$
C
A.$$\frac{n} {2 n-1}$$
B.$$\frac{n} {2 n-3}$$
C.$$\frac{n} {2 n+1}$$
D.$$\frac{n} {2 n+3}$$
7、['数列的定义与概念', '数列的通项公式']正确率80.0%已知数列$${{1}}$$,$${\sqrt {3}}$$,$${\sqrt {5}}$$,$${\sqrt {7}}$$,…,$${\sqrt {{2}{n}{−}{1}}}$$,…,则$${{5}{\sqrt {5}}}$$是它的$${{(}{)}}$$
B
A.第$${{6}{2}}$$项
B.第$${{6}{3}}$$项
C.第$${{6}{4}}$$项
D.第$${{6}{8}}$$项
8、['数列的定义与概念']正确率80.0%已知数列$${{1}}$$,$${{2}}$$,$$\sqrt{7}, \sqrt{1 0}, \sqrt{1 3}, \cdots, \sqrt{3 n-2}$$,⋯中,$${{2}{\sqrt {7}}}$$是这个数列的$${{(}{)}}$$
A
A.第$${{1}{0}}$$项
B.第$${{1}{1}}$$项
C.第$${{1}{2}}$$项
D.第$${{1}{3}}$$项
9、['数列的定义与概念']正确率80.0%已知数列$${{\{}{{a}_{n}}{\}}}$$的通项公式是$$a_{n}=\frac{n} {n^{2}+8} ( n \in N^{*} )$$,则数列的第$${{4}}$$项为$${{(}{)}}$$
B
A.$$\frac{1} {1 0}$$
B.$$\frac{1} {6}$$
C.$$\frac{1} {4}$$
D.$$\frac{1} {3}$$
10、['数列的递推公式', '数列的定义与概念', '数列的通项公式']正确率80.0%已知数列$${{1}}$$,$${\sqrt {3}}$$,$${\sqrt {5}}$$,$${{…}}$$,$${\sqrt {{2}{n}{+}{1}}}$$,$${{…}{…}}$$则$${\sqrt {{2}{1}}}$$是这个数列的$${{(}}$$$${{)}}$$
B
A.第$${{1}{0}}$$项
B.第$${{1}{1}}$$项
C.第$${{1}{2}}$$项
D.第$${{2}{1}}$$项
1. 解析:
根据图像分析数列 $${a_n}$$ 和 $${b_n}$$ 的变化趋势,计算 $${a_n b_n}$$ 的前 $$n$$ 项和 $$S_n$$。通过比较不同 $$n$$ 值下的 $$S_n$$,可以得出 $$S_4 > S_5$$ 且 $$S_{10} < S_{13}$$,因此正确答案是 B。
2. 解析:
观察正整数排列的规律,发现箭头方向呈现周期性变化。从 $$2019$$ 到 $$2021$$ 的箭头方向依次为 $$→$$ 和 $$↓$$,因此正确答案是 B。
3. 解析:
分析数列 $$a_n = \frac{n - \sqrt{2011}}{n - 2012}$$ 的单调性和极值点。通过求导或观察分母变化,发现 $$a_n$$ 在 $$n = 44$$ 时取得最小值,在 $$n = 45$$ 时取得最大值,因此正确答案是 C。
4. 解析:
数列 $$a_n = \frac{3}{3n - 16}$$ 在 $$n = 5$$ 时分母最小,$$a_n$$ 取得最大值;而 $$S_n$$ 随着 $$n$$ 增大趋近于 $$0$$,没有最小值但有最大值,因此正确答案是 A。
5. 解析:
数列 $$3, 9, 27, 81, \dots$$ 是等比数列,通项为 $$3^n$$。$$81 = 3^4$$,因此是第 $$4$$ 项,但选项中没有 $$4$$,可能是题目描述有误。假设题目为 $$3, 6, 9, 12, \dots$$,则 $$81$$ 是第 $$27$$ 项,但选项不符。需进一步确认题目。
6. 解析:
观察数列 $$\frac{1}{3}, \frac{2}{5}, \frac{3}{7}, \frac{4}{9}, \dots$$,分子为 $$n$$,分母为 $$2n + 1$$,因此通项公式为 $$a_n = \frac{n}{2n + 1}$$,正确答案是 C。
7. 解析:
数列通项为 $$\sqrt{2n - 1}$$,设 $$5\sqrt{5} = \sqrt{125}$$,解 $$2n - 1 = 125$$ 得 $$n = 63$$,因此是第 $$63$$ 项,正确答案是 B。
8. 解析:
数列通项为 $$\sqrt{3n - 2}$$,设 $$2\sqrt{7} = \sqrt{28}$$,解 $$3n - 2 = 28$$ 得 $$n = 10$$,因此是第 $$10$$ 项,正确答案是 A。
9. 解析:
代入 $$n = 4$$ 到通项公式 $$a_n = \frac{n}{n^2 + 8}$$,得到 $$a_4 = \frac{4}{16 + 8} = \frac{1}{6}$$,正确答案是 B。
10. 解析:
数列通项为 $$\sqrt{2n + 1}$$,设 $$\sqrt{21}$$ 为某项,解 $$2n + 1 = 21$$ 得 $$n = 10$$,因此是第 $$10$$ 项,正确答案是 A。
.jpg)